MATLAB--基于遗传算法的旅行商问题(TSP问题)实现
MATLAB–基于遗传算法的旅行商问题(TSP问题)实现
在干活的过程中整理下来的,希望对大家有帮助。
什么是旅行商问题:假设有一个旅行商人要拜访全国10个城市,他需要选择所要走的最近路径,路径的限制是每个城市只能访问一次,而且最后要回到原来出发的城市。对路径选择的要求是:所选路径的路程为所有路径之中的最小值。已知10个城市的坐标为[82,7;91,38;83,46;71,44;64,60;68,58;83,69;87,76;74,78;71,71]。在具体操作中一般都采用标号形式表示城市,在计算两城市之间距离时算法能够自动将标号转换成所对应的坐标,来计算两城市之间的距离。
-
1.求解的第一步是根据问题对解空间进行编码
根据TSP问题的具体要求,其解空间应该是遍历所有城市,并且每个城市只能经过一次的路径集合,为此采用序列编码表示法。具体编码规则是每个染色体表示一条可能的旅行路径,由按一定顺序排列的10个城市的序号组成,染色体中的每个基因表示一个城市,染色体的长度为需要遍历的城市数10。例如,3→2→5→4→10→7→1→6→9→8→3为一条路径,用序列编码表示法可简单表示为[3 2 5 4 10 7 1 6 9 8],其含义为从城市3出发依次经过城市2、5、4、10、7、1、6、9、8然后返回城市3的一条路径。这种编码方式满足TSP问题的约束条件,保证了每个城市都经过且只经过一次,并且保证任何一个城市子集中不形成回路,同时在计算个体的适应度函数值时无需解码,变异算子也容易设计。坐标的位置与城市的标号是一一对应的,其中第一个坐标(82, 7)表示标号为1的城市坐标,第二个坐标(91, 38)表示标号为2的城市坐标,以此类推第10个坐标(71, 71)表示标号为10的城市坐标。 -
2.求解的第二步是生成初始种群
遗传算法一般都是随机生成初始种群。在MATLAB语言中可调用函数randperm(),对于10城市的TSP问题,randperm(10)能够随机生成一个由1~10数字组成的无重复序列,代表遍历所有城市的一条路径,存入矩阵Road中。矩阵Road是一个SizeScale×n的矩阵,其中SizeScale是种群规模的大小,表示初始种群有多少条路径;n是每个染色体中的基因数,为需要遍历的城市数10,Road(i,:)代表初始种群路径矩阵中的第i行,表示第i条路径。矩阵Road是一个动态矩阵,选择、交叉和变异操作后的结果都将反复存储在这个矩阵中。
种群规模的大小直接影响遗传优化的结果和效率,通常要根据问题的解空间来选取。种群的规模过小时将增加最大进化迭代次数,种群的规模过大时将增加每一次迭代的计算量,因此种群的规模应该进行多次实验后确定一个折中值。10城市的TSP问题的解空间为10!=3628800,根据以往经验,本例中取种群规模为150,那么Road是一个150×10的矩阵。这里我用的是MATLAB 2016b编写的程序。主程序设计的比较简单,算法的实现主要在tapga.m中。下边的第一段是主程序,tapga.m在文章的最后。tapga.m第17行生成了一个MaxIter×1的全1矩阵MinestRoad_fval,用来保存每一次迭代得到的最短里程。程序第18行生成了一个MaxIter×n的全1矩阵MinestRoad_opt,用来保存每一次迭代得到的最短里程对应的路径。
Map1=[82,7;91,38;83,46;71,44;64,60;68,58;
83,69;87,76;74,78;71,71];%具体城市坐标
MaxIter=200; %最大迭代次数
Pop_Size=150; %种群规模
pc=0.8; %选择概率
pm=0.1; %变异概率
[opt,fval]=tspga(Map1,MaxIter,Pop_Size,pm,pc);
- 3.第三步:适应度值的计算
TSP问题要求遍历所有城市的里程最短,因此其最优适应度值应该是遍历所有城市并且每个城市只遍历一次的里程最小值。而遗传算法是解决最大值问题,为此需要进行有效的变换,将求解最小值问题转换成求解最大值问题,采用如下图的变换将其转换成最大值问题。
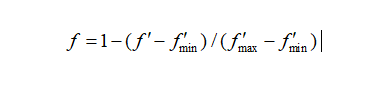
MATLAB程序实现如下。
function f=fitness(fmin,fmax,froad)
f=1-(froad-fmin)/(fmax-fmin); %适应度函数
end
程序中froad为两个城市之间的距离,计算公式如下图所示,

MATLAB程序实现如下。
function d=distance(A,B)
d=sqrt((A(1)-B(1))^2+(A(2)-B(2))^2); %距离公式
end
计算出每两个城市之间的距离存储于距离矩阵DistMatrix中。
迭代开始后,首先计算每条路径的里程。用一个for循环调出矩阵Road中的所有路径,再用一个for循环将每一路径中相邻两城市之间距离累加,可以得到种群中每条路径的里程,存储于矩阵Dist中,它是一个 的矩阵,即Dist(i)中存储路径i的里程。
然后,根据每条路径的里程,即可计算适应度值。
在tapga.m程序中,矩阵MinRoad为通过min函数求得的种群中最短路径的里程,矩阵MaxRoad为通过max函数求得的种群中最长路径的里程。将矩阵Dist中最短里程及对应的路径序号存储为MinRoad和A,调用前面编写的函数fitness,计算每条路径的适应度值,存储在矩阵fitmatrix中。
-
4.求解的第四步是进行遗传算子操作
遗传算子有选择、交叉、变异三个操作,先介绍如何进行选择算子操作。
(1)选择算子操作
在本例中,采用的方法就是找出种群中适应度值的最大值和最小值,去除最小值对应的染色体,用最大值对应的染色体代替,从而产生新的种群。调用函数sort对适应度值进行排序,返回值c中存放升序排列适应度的值,p中存放的是c对矩阵fitmatrix()的索引,即适应度值对应的fitmatrix()中的第几行。选出20个适应度值最小的路径,用适应度值最大的那条路径代替他们。(2)交叉算子操作
TSP问题对交叉运算有特殊要求。因为TSP问题要求遍历所有城市,并且每个城市只能经过一次。为了避免染色体所表示的路径出现重复经过一个城市的现象,在这里采用书中介绍的顺序的交叉的方式。具体操作如下。
步骤1:随机选取两个父代染色体 和 ,随机选择出两个切点X和Y,如取X=1,Y=4为例,分别得到A、 中两个对应的基因序列段为 以及 ,具体如下图所示。

在MATLAB程序中,randi([1 SizeScale], 2, 1)产生2*1的矩阵,矩阵中每个元素大小在1到150之间,当随机数rand(1)小于交叉概率时,进行交叉操作。oldp1和oldp2为随机选取的两个父代染色体,crossj1和crossj2是随机选取的连个切点,segment1和segment2分别是oldp1和oldp2被选中的基因序列段。
步骤2:在A中从第一个元素开始搜索,遇到与 中相同的元素则从A中删除,得到 。同理,在B中删除 中的元素得到 ,如下图所示:

MATLAB子函数eliminate,去除x中与y相同的元素。
function elim=eliminate(x,y)
for n=1:length(y)
x=x(find(x~=y(n))); %去除x中的y
end
elim=x;
end
调用函数eliminate,去除oldp1中与segment2相同的元素,去除oldp2中与segment1相同的元素。
步骤3:得到子代染色体 ,如下图所示:

交叉操作结束之后,将交叉后的子代染色体存入路径矩阵Road1中。交叉操作后,重复适应度值计算的操作,更新里程矩阵Dist,将最短里程及对应的路径序号存储为MinRoad2和B,并计算交叉操作后种群的适应度值。
(3)变异算子操作
与交叉操作相同,变异操作之后每条路径不能有重复城市出现,因此采用与交叉方式相似的操作。首先对种群适应度函数进行升序排列,对于种群中的每一个染色体,随机选取两个变异点pos1和pos2,如果随机数rand()小于变异概率并且该染色体没有最大的适应度值,则对该染色体进行变异操作,将该染色体的两个变异点对应的基因进行互换,即可生成一个新的染色体。
交叉操作后,重复适应度值计算的操作,更新里程矩阵Dist,将最短里程及对应的路径序号存储为MinRoad3和C。MATLAB程序实现如下。
(4)搜索每一代的最优路径
使用嵌套的if语句,两两比较MinRoad、MinRoad2、MinRoad3,将三者中的最小值存储为MinestRoad,将对应的路径序号存储为D,对应点路径存储在Road(D,:)中。
MinestRoad即为本次迭代最小里程值,存储在MinestRoad_fval(iter,1)中,Road(D,:) 为本次迭代最小里程值对应的路径,存储在MinestRoad_opt(iter,:)中,更新路径矩阵Road,
重复迭代,直到迭代次数达到最大迭代次数。
- 5.求解的最后一步是输出结果及绘图
调用min函数,取里程的最小值存储为MinestRoad,对应点迭代次数存储为a,输出最短里程MinestRoad,最优路径MinestRoad_opt(a,:),及对应点迭代次数a
调用plot函数,绘制城市地图,每个城市用*表示出来,之后用hold on命令来使当前坐标轴及图形保持不变,然后调用text函数,将每个城市标号,颜色为黑色,字体为黑体。 - 下面给出tapga.m的程序。
%遗传算法计算TSP
function [opt,fval]=tspga(Map,MaxIter,SizeScale,pm,pc)
n=max(size(Map));
DistMatrix=zeros(n,n);%初始化距离矩阵DistMatrix(),用于存储两城市之间距离
for i=1:n
for j=1:n
DistMatrix(i,j)=distance(Map(i,:),Map(j,:));%计算两城市之间距离,存储于DistMatrix()矩阵中
end
end
%%%%%%%%%生成初始种群%%%%%%%%%%%
Road=ones(SizeScale,n);%初始化路径矩阵Road()
for i=1:SizeScale
Road(i,:)=randperm(n);%随机生成初始种群(路径矩阵)
end
iter=1;
MinestRoad_fval=ones(MaxIter,1);%初始化最短里程矩阵MinestRoad_fval()的历史记录值
MinestRoad_opt=ones(MaxIter,n);%初始化最短里程路径矩阵MinestRoad_opt()的历史记录值
while iter<=MaxIter
Dist=zeros(SizeScale,1);%初始化里程矩阵Dist,用于存储每条路径的里程值
%%%%%%计算每条路径的里程%%%%%
for i=1:SizeScale
for j=1:(n-1)
Dist(i)=Dist(i)+DistMatrix(Road(i,j),Road(i,j+1));
end
Dist(i)=Dist(i)+DistMatrix(Road(i,1),Road(i,n));%计算每条路径的里程存储于Dist()矩阵中
end
%%%%%%%%计算每条路径的适应度值%%%%%%%%%
fitmatrix=ones(SizeScale,1);
[MinRoad A]=min(Dist(:,1));%计算出最小里程值
MaxRoad=max(Dist(:,1)); %计算出最大里程值
for i=1:SizeScale
fitmatrix(i)=fitness(MinRoad,MaxRoad,Dist(i));%计算每条路径的适应度的值,存储于fitmatrix()中
end
%%%%%%%%%%选择操作%%%%%%%%%
[c p]=sort(fitmatrix(:,1));%对适应度值进行升序排列,c中存放升序排列适应度的值,
%p中存放的是c对fitmatrix()的索引,即适应度值对应的fitmatrix()中的第几行
change=20;%选出适应度值最小路径数目
for i=1:change
Road(p(i),:)=Road(p(SizeScale),:);%选出适应度值最小的20条路径,用适应度值最大的路径替换
end
Roadnew=Road;
%%%%%%%%%%%%交叉操作%%%%%%%%%%%%
for i=1:SizeScale
u=randi([1 SizeScale],2,1);
s=u(1);
t=u(2);
if rand(1)MinRoad)&&(MinRoad3>MinRoad)
MinestRoad=MinRoad;
D=A;
Road(D,:)=Road(A,:);
else
if (MinRoad>MinRoad2)&&(MinRoad3>MinRoad2)
MinestRoad=MinRoad2;
D=B;
Road(D,:)=Roadnew(B,:);
else
MinestRoad=MinRoad3;
D=C;
Road(D,:)=Road1(C,:);
end
end
MinestRoad_fval(iter,1)=MinestRoad;%本代最小里程值
MinestRoad_opt(iter,:)=Road(D,:);%本代最优路径
iter=iter+1;
Road=Road1;
end
[MinestRoad a]=min(MinestRoad_fval);%取路径里程最小值
opt=MinestRoad_opt(a,:)%输出最优路径
fval=MinestRoad%输出最短里程
A=a%得到最优路径的迭代次数
%%%%%%%%%%绘图%%%%%%%%%
plot(Map(:,1),Map(:,2),'*');
hold on
for c = 1:n
text(Map(c, 1), Map(c, 2), [' ' num2str(c)], 'Color', 'k', 'FontWeight', 'b');
end
XX=Map(MinestRoad_opt(a,:),1);
XX=[XX;Map(MinestRoad_opt(a,1),1)];
YY=Map(MinestRoad_opt(a,:),2);
YY=[YY;Map(MinestRoad_opt(a,1),2)];
plot(XX,YY);
legend('城市','最优路径');
end
程序有的部分是根据各种资料整理、然后加上我的改进,出处不详,如果有侵权的请私聊我,我注明出处。