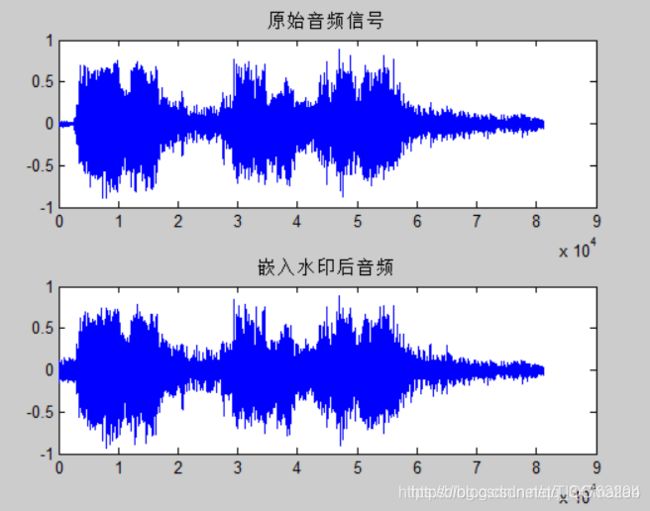
【信号处理】基于matlab小波变换的音频水印嵌入提取【含Matlab源码 053期】

一、简介

较早利用分块DCT的水印技术，他们的水印方案是用一个密钥随机的选择图像的一些分块，在频域的中频上稍稍改变一个三元组来隐藏二进制序列信息。这种方法对有损压缩和低通滤波是稳健的。Cox等[提出了着名的基于图像全局变换的数字水印技术，该方案对整个图像作离散余弦变换（DCT），Barni等提出一种利用HVS掩蔽特性的基于DCT的水印算法，在水印嵌入阶段，对 的图像进行 的DCT变换，对DCT系数按Zig-Zag扫描重新排列为一维向量，留下向量中开始的L个系数不作修改，对第L个系数后面的M个系数进行修改以嵌入水印。黄继武等人 在对DCT系数DC和AC分量的定性和定量分析的基础上，指出DC分量比AC分量更适合嵌入水印，嵌入DC分量的水印具有更好的稳健性，并提出了一个利用DC分量的自适应算法。

数字水印（Digital Watermarking）技术是将一些标识信息（即数字水印）直接嵌入数字载体当中（包括多媒体、文档、软件等）或是间接表示（修改特定区域的结构），且不影响原载体的使用价值，也不容易被探知和再次修改。但可以被生产方识别和辨认。通过这些隐藏在载体中的信息，可以达到确认内容创建者、购买者、传送隐秘信息或者判断载体是否被篡改等目的。数字水印是信息隐藏技术的一个重要研究方向。 数字水印是实现版权保护的有效办法，是信息隐藏技术研究领域的重要分支。本文简单介绍了数字水印的几种重要算法，提出了一个基于离散小波变换（DWT）的音频数字水印模型，并给出了部分实验结果。

1 音频水印

音频数字水印的主要应用是隐蔽通信及版权保护。隐蔽通信注重信息的隐匿以及数据的嵌入容量，版权保护则强调稳健性。目前应用于音频产品数字版权保护的水印技术大多局限于非压缩域，包括时域和变换域。时域主要有LSB算法和回声算法，变换域算法则主要采用DCT、DFT以及DWT。

音频嵌入数字水印比较重要的算法有以下几类：

（1）最不显着位嵌入（LSB－Lesat Significant Bit）是一种最简单的嵌入方法。任何形式的水印均可以转换成一串二进制的码流。音频文件的每一个采样数据也是用二进制数值加以表示的。这样可以通过将每一个采样值的最不显着位（通常为最低位），用代表水印的二进制位替换，即可在音频信号中嵌入水印。如果将音频信号看作水印传输的信道，水印看作在信道中传输的信号，理想情况下，信道容量将是1Kbps/kHz，即采样率和比特率在数值上相当。伪随机序列可以由伪随机序列发生器产生。当伪随机序列发生器具有固定结构时，不同的初始值会产生不同的伪随机序列，这样收发双方只需要秘密传送一个初值作为密匙而不必传送整个伪随机序列值。为增强水印稳健性，可考虑将水印加到音频数据的高频分量上。

LSB法简单易行，数据容量大，安全性较高。缺点是对抗信号处理的稳健性差。

（2）扩频方法（Spread Sprectrum Encoding）。此方法是将编码数据分布到尽可能多的频谱中对信息流进行编码。常用的有直接序列扩频编码（DSSS），它通常结合性能优良的m序列进行编码和解码。为了利用HAS的掩蔽效应，一般需要对所采用的序列进行若干级的滤波处理，水印的检测则结合相关性假设检验检测方法。该方法对MP3音频编码、PCM量化以及附加噪声有一定的稳健性。扩频方法具有抗干扰性能好，隐蔽性强、干扰小，易于实现码分多址，数模兼容。

（3）相位编码。利用人耳听觉系统对绝对相位不敏感以及对相对相位敏感的特性，使用代表水印信息的参考相位替代原始音频段的绝对相位，并调整其余音频段以保持相对相位的不变。其编码步骤简述如下：

⑥根据修改后得到的相位矩阵和原始幅度矩阵，进行IDFT逆变换，生成含有水印的音频信号。

（4）回声隐藏。通过引入回声将水印数据嵌入到音频信号，其中利用了HAS的另一特性：音频信号在时域的向后屏蔽作用，即弱信号在强信号消失之后被屏蔽，大约在强信号消失之后的50ms～200ms之内继续作用而不被人耳所察觉。

由于回声隐藏是将水印信息作为载体数据的环境而非随机噪声嵌入到载体数据中，因此对一些有损压缩的算法有令人满意的稳健性。

（5）变换域算法：变换域算法具有许多空域算法所不具备的优点，其中最突出的一点是其算法的稳健性。变换域算法包括离散傅立叶变化（DFT）、离散余弦变换（DCT）以及近年来兴起的离散小波变换（DWT）。对于前二种方法，国内外已经做了相当多的研究，基本思想都是结合HAS听觉特性对原始音频数据在一定的频域内进行变换处理，然后改变相应的变换系数来嵌入水印。本文的算法是基于第三种变换即离散小波变换的。这里简单介绍一下DWT技术。

DWL算法是利用Daubechies-4小波基的原始音频进行L级的小波分解，保留前L-1级的差别分量而对第L级的细节分量进行处理并嵌入水印。此算法的一个特点是将水印信号放在语音信号能量最集中的低频部分。

2 人类听觉模型

人类听觉系统对于输入信号所作出的反应是基于频率的，音调的不同对应于频率的变化。图1所示即为人耳的灵敏度对于频率的函数，图中给出了可为人耳所听到的最低声音强度，对于每个不同频率正好就是音频灵敏度的倒数。从图1可知，人耳对于3kHz左右的频率最为敏感，对于过高（20kHz）以及过低（20Hz）的频率，人耳敏感性将降低。

根据这一特性可知：水印嵌入到音频数据的合适的高频或者低频分量上，都可以合理预期不破坏原始音频的质量。这一点可从后续试验中得到验证。

3 算 法

本算法采用DWT，包含水印嵌入、水印检测以及水印攻击三个主要部分。水印的工作原理如图2所示。水印的检测需要原始音频数据。

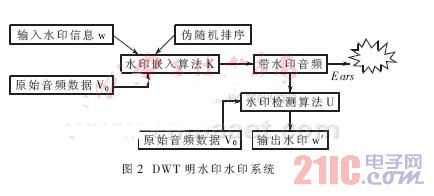
3.1 水印嵌入算法

（1）将待嵌入水印图像置乱。本算法简单地采用伪随机数算法消除数据的相关性。（2）将原始音频数据进行多尺度一维分解，并分别提取低频系数和三层高频系数。为获取较好的稳健性，本算法将水印数据嵌入到音频数据的第三层高频分量上。（3）根据公式Vw（i）=V（i）+（α+e）×W（i）嵌入水印数据。其中V（i）为音频数据位，W（i）为水印数据位，Vw（i）为嵌入水印后的音频数据位，α为水印嵌入强度，e值作为修正，取值10-20。通过试验，发现α值取为0.004时嵌入水印效果较为理想。（4）将嵌入水印数据后的音频进行IDWT变换，即得到包含水印的音频数据。

3.2 水印检测算法

（1）将含有水印的音频数据进行多尺度一维分解，并提取其三层高频分量系数。

（2）检测算法为嵌入算法的逆过程，需要原始音频数据参与检测，表达为：

W（i）=（Vw（i）-V（i））/（α+e），其中α以及e的值同嵌入算法中确定的值一致。

（3）步骤（2）得到的W（i）即为提取的一维水印信息序列，将其进行升维处理，可以得到二维图像形式。此结果便是检测输出的水印。

嵌入水印的原图及一次嵌入后提取的水印分别如图3和图4所示。

4 部分试验

为测试本水印系统的性能，对加水印的音频数据进行各类攻击，这里给出部分实验结果。

定义：

Nc作为衡量所提取水印图像与原始水印图像的相似程度，从未被攻击的含水印音频中直接提取的水印与原水印图像相似度高达0.9998。

（1）二选一迫选实验。对事先不知道精确原始音频信号的测试者分别播放原始音频和嵌入水印后的音频，要求测试者指认原始音频。根据L.BONey等[5]的结论，如果二类音频被指认为原始音频的比例大致相当，则可认为水印嵌入后没有引起人耳感知上的显着差别。试验中随机选取同实验室学生8人，通过分别在不同wav文件中嵌入水印并随机询问的方法，结果约有53.4%的接受询问者认为原始音频音质更好。说明通过本系统嵌入的水印没有引起原始音频音质上的显着改变。

（2）将音频截掉全部数据的n/10（n=1，2，3……），原始音频数据位长度稍大于40 000，从第20 000位开始剪切。

根据图5、图6、图7可知将音频剪切掉约三分之一内容后，仍可提取出较为明显的水印图案。如果剪切部分再多一些，则无法满意地检测出水印。但由于三分之一的剪切率将同时导致载体音频数据的大量丢失，故这个结果是可以接受的。

（3）MP3压缩。目前对音频信号进行MP3压缩编码是较为常用的一种音频处理技术，其目标为在不影响原始音频信号品质的前提下尽可能地减少音频数据量。不同的比特率对应了不同的MP3压缩比。本试验对上面含有水印的一段音频先进行码率为96Kbps的压缩（压缩比为7.4：1），然后进行相映解码处理，检测得到的水印图像如图8所示。

5 结 论

近年来音频数字水印领域尤其是变换域音频水印嵌入与检测方面的研究工作发展迅速，而离散小波分析（DWT）是近年来整个数字水印系统研究的热点之一。算法经实验表明具有很好的隐蔽性，对原始音频的质量几乎没有削弱，具备一定的抵抗剪切攻击及其他攻击的能力。为进一步提高算法的稳健性，应该进一步考虑如何利用更多HAS特性以及水印嵌入的位置和强度。顾及算法实用性，应当考虑增加嵌入水印的容量问题。这些都是需进一步改善的方向。

二、源代码

clear all;
clc;
key=35;
%Arnold置换次数，作为密钥
Orignalmark=double(imread('suda64.bmp'));  %读入64*64的水印图片
[wrow,wcol]=size(Orignalmark);  
if wrow~=wcol 
    error('wrow~=wcol error');
end
%--- 测试密钥key是否超出范围---------
n=check_arnold(wrow);
if (key+1)>n
    error('arnold key error');
end
Arnoldw=arnold(Orignalmark,wrow,key); %对水印图像进行Arnold转化
[X,fs,bits]=wavread('laile.wav'); %读入音频文件
%X=imread('lena.bmp');
figure;    
subplot(2,1,1); 
%imshow(X),title('原始图像');
%X=double(X);
plot(X);     %显示音频文件波形
title('原始音频信号'); 
%sound(X,fs,bits);
%pause;
%水印嵌入--------------------------------------------------
[c,l]=wavedec(X,2,'db4'); %用db4小波对读入的声音文件进行2级小波分解 
ca2=appcoef(c,l,'db4',2); %提取2级小波分解的低频系数和高频系数 
cd2=detcoef(c,l,2); 
cd1=detcoef(c,l,1); 
lca=length(ca2);  %低频长度
blocksize=fix(lca/(wrow*wcol)); %每块的大小
water_vector=reshape(Arnoldw,1,wrow*wcol);  %将置乱后的水印转化为一维的
wlength=wrow*wcol;  %水印的长度
a=0.25;  %量化步长
j=1;
for i=1:wlength
    Block=ca2(j:j+blocksize-1);
    [U,S,V]=svd(double(Block)); 
    cc=floor(S(1,1)/a);  
    if(Arnoldw(i)==1)           %嵌入奇数倍
        if(mod(cc,2)==0)
            cc=cc+1;
        end
        S(1,1)=a*cc;
    end
    if(Arnoldw(i)==0)            %嵌入偶数倍
        if(mod(cc,2)==1)  
            cc=cc+1;
        end
        S(1,1)=a*cc;
    end
    Blockw=U*S*V';          %SVD 逆变换还原 
    ca2(j:j+blocksize-1)=Blockw; 
    j=j+blocksize;
end
c1=[ca2',cd2',cd1']';
 
 
 

三、运行结果

四、备注

完整代码或者代写添加QQ2449341593
往期回顾>>>>>>
【信号处理】基于matlab HMM的睡眠状态检测【含Matlab源码 050期】
【信号处理】基于matlab CDR噪声和混响抑制【含Matlab源码 051期】
【信号处理】基于matlab最小二乘法解决稀疏信号恢复问题【含Matlab源码 052期】