《DLS》第二章笔记:感知机
《DLS》第二章笔记:感知机
2.1 感知机
2.1.1 神经元
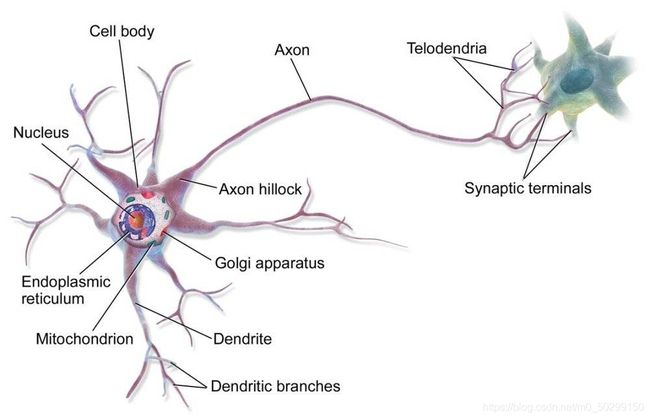
对于生物学意义上的神经元,一个神经元具有多个树突接收输入信号,一个细胞主体处理输入信号,一个轴突传递输出信号,如下图:
将神经元抽象为一个算法模型:
我们将这个模型称为人工神经元,也称感知机。
2.1.2 感知机的组成
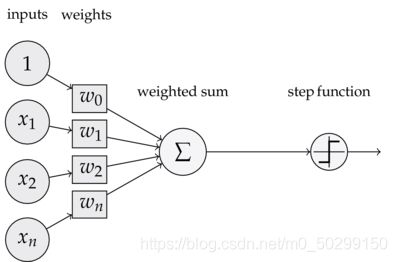
一个感知机由输入权值、激活函数、输出三部分组成。
y = { 0 , ( b + w 1 x 1 + w 2 w 2 + . . . + w n x n ≤ 0 ) 1 , ( b + w 1 x 1 + w 2 w 2 + . . . + w n x n > 0 ) y=\begin{cases} 0,(b+w_{1}x_{1}+w_{2}w_{2}+...+w_{n}x_{n}\leq 0)\\ 1,(b+w_{1}x_{1}+w_{2}w_{2}+...+w_{n}x_{n}>0)\\ \end{cases} y={ 0,(b+w1x1+w2w2+...+wnxn≤0)1,(b+w1x1+w2w2+...+wnxn>0)
输入权值:一个感知机可以接收多个输入 x 1 , x 2 , . . . , x n ( x i ∈ R ) x_{1},x_{2},...,x_{n}(x_{i}\in\mathbb{R}) x1,x2,...,xn(xi∈R),每个输入上有一个权重值 w i ∈ R w_{i}\in\mathbb{R} wi∈R,此外还有一个偏置项 b ∈ R b\in\mathbb{R} b∈R,即 w 0 w_{0} w0。输入信号被送往神经元时会被分别乘以固定的权重。
(权重是控制输入信号重要性的参数,偏置是调整神经元被激活的容易程度的参数)
激活函数: f ( x ) f(x) f(x) 决定如何来计算输入信号的总和。只有当总和超过某个界限时,才会输出1,即“神经元被激活”,这个界限值被称为阈值。
输出:输出 y = f ( x ) y=f(x) y=f(x),输出值只有两个,即0或1。总和超过阈值时输出1,总和未超过阈值时输出0。
2.1.3 神经元和感知机的对应关系
| 神经元 | 感知机 |
|---|---|
| 树突接收的信号 | 输入权值 |
| 细胞主体 | 激活函数 |
| 轴突输出的信号 | 输出 |
2.2 逻辑门
2.2.1 与门
与门对应逻辑运算“与”,真值表如下:
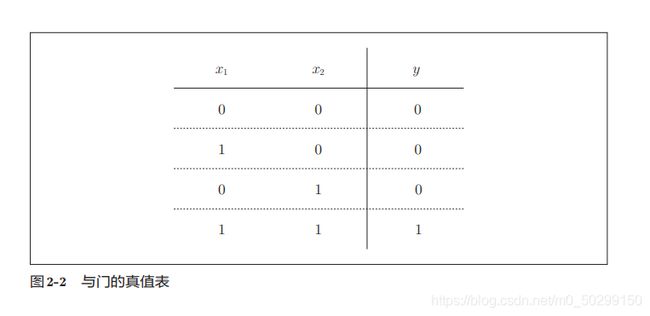
用感知机实现与门,实际上就是寻找一组能满足与门真值表的 w 1 w_{1} w1、 w 2 w_{2} w2、 θ \theta θ的值。这样的值有无数多个,选择不同的值就是选择不同的权重。
Python实现:
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
x1, x2 = map(int, input().split())
print(AND(x1, x2))
C++实现:
#include2.2.2 与非门
与非门对应逻辑运算“与”和“非”,真值表如下:
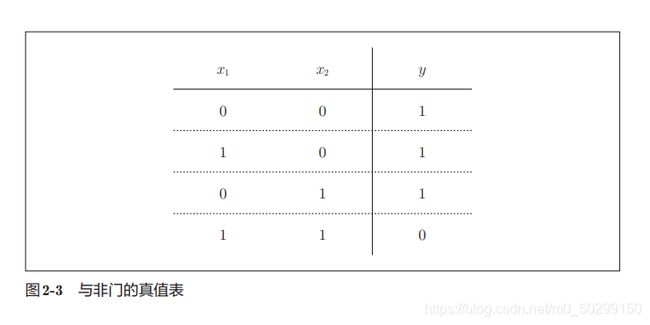
与非门的输出实际上就是颠倒了与门的输出,只要把实现与门的参数值 w 1 w_{1} w1、 w 2 w_{2} w2、 θ \theta θ取反就可以实现与非门。
Python实现:
import numpy as np
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
x1, x2 = map(int, input().split())
print(AND(x1, x2))
C++实现:
#include2.2.3 或门
或门对应逻辑运算“或”,真值表如下:
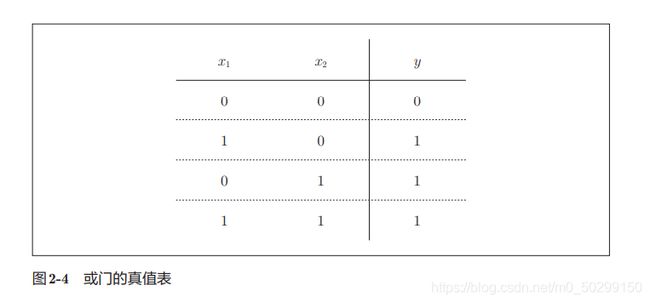
用感知机实现或门,实际上就是寻找一组能满足或门真值表的 w 1 w_{1} w1、 w 2 w_{2} w2、 θ \theta θ的值。这样的值有无数多个,选择不同的值就是选择不同的权重。
Python实现:
import numpy as np
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
x1, x2 = map(int, input().split())
print(AND(x1, x2))
C++实现:
#include与门、与非门和或门是具有相同结构的感知机,区别只在于权重参数的值。
2.2.4 异或门
异或门对应逻辑运算“异或”,真值表如下:
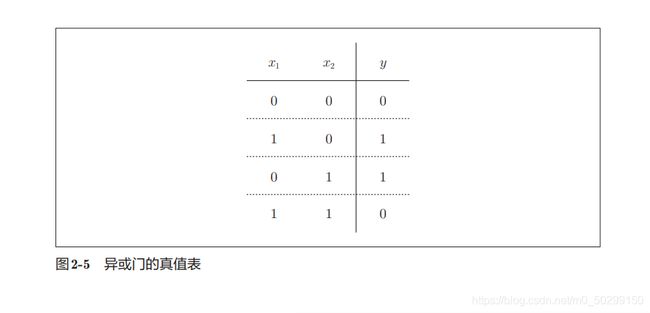
异或(XOR)的运算是特性是“相同为0,不同为1”,即仅当 x 1 x_{1} x1或 x 2 x_{2} x2中的一方为1时,才会输出1(“异或”是拒绝其他的意思)。简单实践就可发现,我们无法用单层感知机实现异或门。
2.3 多层感知机
2.3.1或门可视化
对于或门
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
表示 y = { 0 , ( − 0.5 + x 1 + w 2 ≤ 0 ) 1 , ( − 0.5 + x 1 + w 2 > 0 ) y=\begin{cases} 0,(-0.5+x_{1}+w_{2}\leq 0)\\ 1,(-0.5+x_{1}+w_{2}>0)\\ \end{cases} y={ 0,(−0.5+x1+w2≤0)1,(−0.5+x1+w2>0)
即,坐标系被直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1,另一个空间输出0。
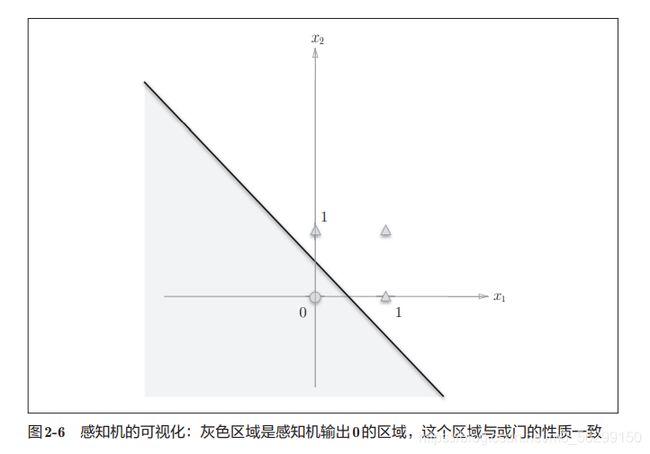
2.3.2异或门可视化
对于异或门
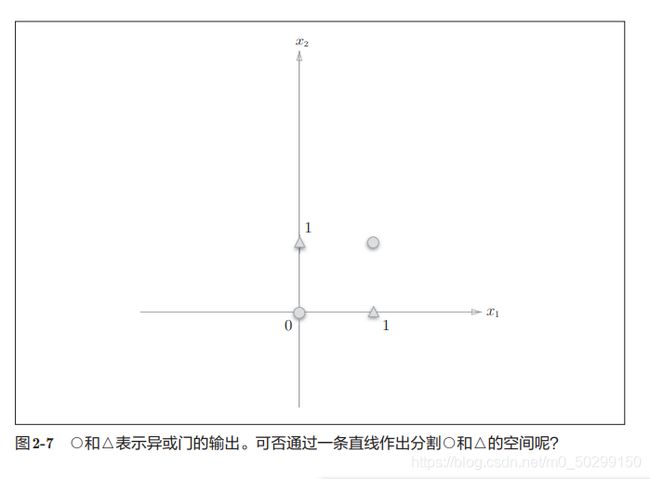
显然,无法使用一条直线把三角和圆圈分割开来,考虑:
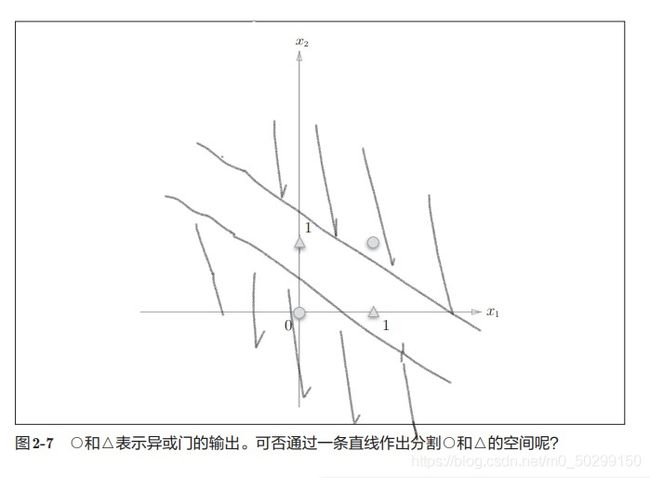
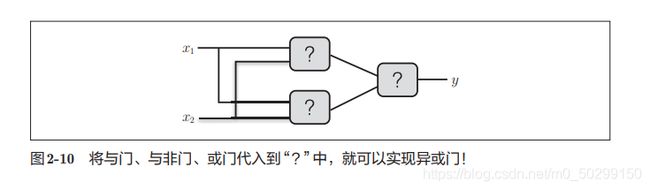
即通过与门、或门、与非门的组合来实现异或门。
寻找实现异或门的组合:
2.3.3 异或门的实现
列出与门的真值表:
| x 1 x_{1} x1 | x 2 x_{2} x2 | y y y (AND) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
列出与非门的真值表:
| x 1 x_{1} x1 | x 2 x_{2} x2 | s 1 s_{1} s1 (NAND) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
列出或门的真值表:
| x 1 x_{1} x1 | x 2 x_{2} x2 | s 2 s_{2} s2 (OR) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
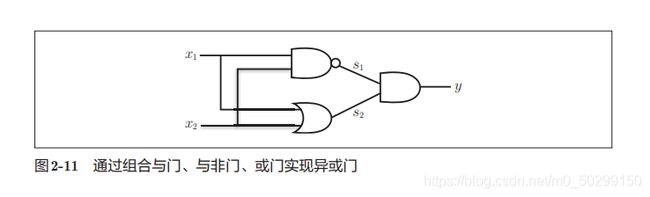
则可发现:
| s 1 s_{1} s1(NAND) | s 2 s_{2} s2(OR) | y y y (AND) |
|---|---|---|
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
import numpy as np
def AND(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.5,0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
x1, x2 = map(int, input().split())
print(XOR(x1, x2))
C++实现:
#include2.3.4 多层感知机
叠加了超过两层的感知机被称为多层感知机,异或门就是通过双层感知机实现的。多层感知机可以实现单层感知机实现不了的结构,通过叠加层(加深层),感知机能进行更加灵活的表示。
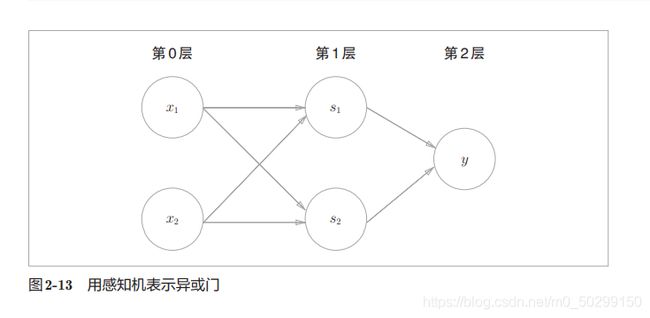
上图所示的2层感知机中,先在第0层和第1层的神经元之间进行信号的传送和接收,然后在第1层和第2层之间进行信号的传送和接收,具体如下所示:
1.第0层的两个神经元接收输入信号,并将信号发送至第1层的神经元。
2.第1层的神经元将信号发送至第2层的神经元,第2层的神经元输出y。
2.4 感知机和计算机
两层感知机(使用sigmoid函数为激活函数)就可以表示任意函数。
《计算机系统要素:从零开始构建现代计算机》:以深入理解计算机为主题,论述了仅通过 NAND构建可运行俄罗斯方块的计算机的过程。