4车道线检测实现-4.1相机校正
学习目标
- 了解相机的成像原理
- 了解相机标定的分类,原理和意义
- 了解图像畸变
- 知道相机标定过程中的坐标系
- 知道张氏标定法的原理及实现
- 了解双目校正
4.0国内外检测车道线的方法主要有两类:一类是基于模型的检测方法,还有一类是基于特征的检测方法。
- 基于模型的检测方法是将车道赋予一种合适的数学模型,并基于该模型对车道线进行拟合,原理就是在结构化的道路上根据车道线的几何特征为车道线匹配合适的曲线模型,在采用最小二乘法,Hough变换等方法对车道线进行拟合。常用的数学模型有直线型、抛物线模型以及样条曲线模型。这种方法对噪声抗干扰能力强。但也存在弊端,即一种车道线模型不能同时适应多种道路场景。
- 基于特征的检测方法是根据车道线自身的特征信息,通过边缘检测或者阈值分割将车道线的特征信息从路面区域中提取出来。该方法对车道线的边缘特征要求较高,在边缘特征明显的情况下可获得较好的结果,但对噪声很敏感,鲁棒性较差。
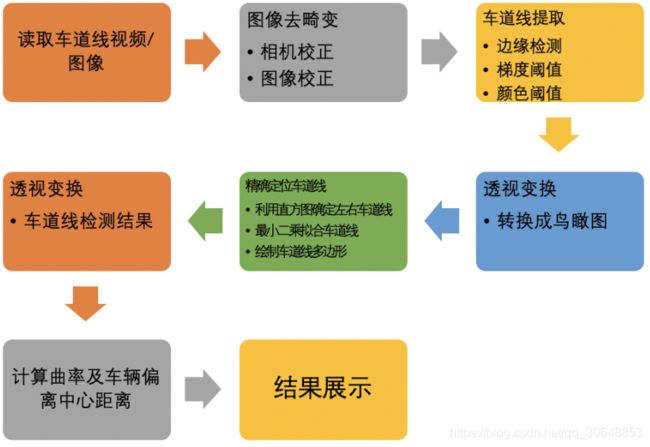
本项目针对车载相机获得的道路图像进行提取,主要是对图像进行校正,利用边缘提取和颜色阈值的方法提取车道线,利用透视变换将图像转换为鸟瞰图,利用直方图统计的方法确定左右车道位置,并利用最小二乘法拟合车道线,并利用透视变换将检测结果绘制在图像上,最后计算车道线的曲率及车辆偏离车道中央的距离,流程如下图所示:
1.相机标定:
相机标定的一个目的就是建立像素坐标系和世界坐标系之间的关系。原理是根据摄像机的模型,由已知特征点的图像坐标求解摄像机的模型参数,并求出成像的反过程,从而从图像中恢复出空间点的三维坐标,达到三维重建的目的。相机标定还可以进行图像校正,由于透镜的制造精度以及组装工艺的偏差会引入畸变,导致图形失真,所以我们可以求解畸变参数,对图像进行去畸变。(要找一个合适的数学模型,求出这个模型的参数,能够近似从三维到二维的过程,使这个三维到二维的过程的函数找到反函数。)
标定之后通过内外参数去畸变。个人理解标定是根据畸变的图片和正常的图片(三维世界图片)的特征提取求出参数,再去畸变
6.张氏标定法
2.成像原理
小孔成像是利用了光线直线传播的原理。
3. 相机成像模型
世界坐标系(X_W,Y_W,Z_W)(XW,YW,ZW):是目标物体位置的参考系。单位为长度单位,比如说m。
在双目视觉中世界坐标系主要有三个用途:
相机坐标系(X_C,Y_C,Z_C)(XC,YC,ZC):是相机站在自己的角度衡量物体的坐标系。单位为长度单位,如mm。
图像坐标系(x,y):以图像平面的中心为坐标原点,物理单位(例如毫米)表示像素在图像中的位置。
像素坐标系(u,v) 以图像平面的左上角顶点为原点,以像素为单位的图像坐标系.(四大坐标系)
3.1. 世界坐标系与相机坐标系之间的转换
世界坐标系转换到相机坐标系未发生形变,作平移和旋转。外参。
3.2. 相机坐标系到图像坐标系的转换
从3d到2d的过程,属于透射投影关系。内参。三维重建
3.3. 图像坐标系到像素坐标系
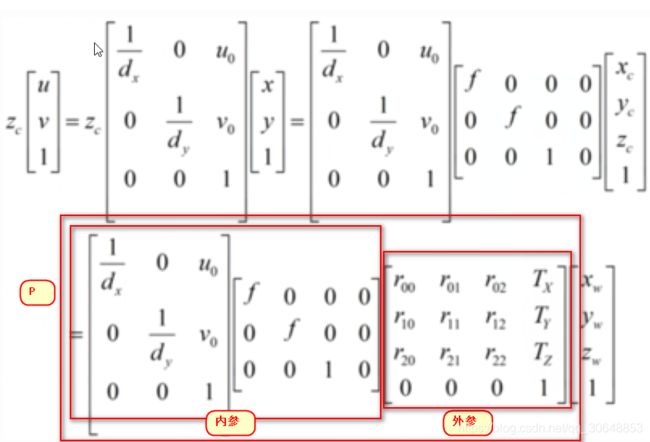
总结
内参:描述相机内部属性的参数,确定相机从三维空间到二维图像的投影关系,畸变系数也属于内参,我们在下面进行介绍。
外参:决定相机坐标与世界坐标系之间相对位置关系,主要包括旋转和平移两部分。
4. 图像畸变
4.1. 径向畸变
径向畸变就是沿着透镜半径方向分布的畸变,产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲,这种畸变在普通的镜头中表现更加明显,径向畸变主要包括桶形畸变和枕形畸变两种。
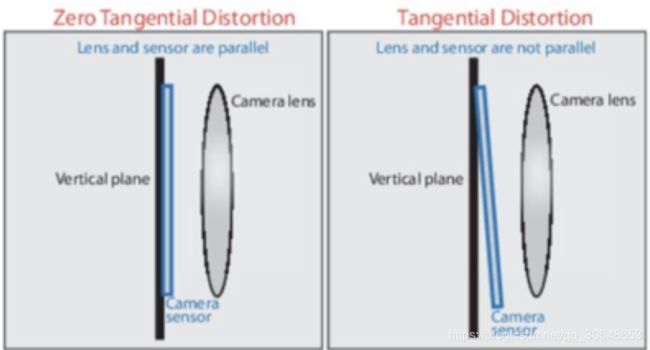
4.2. 切向畸变
切向畸变是由于透镜本身与相机传感器平面(像平面)或图像平面不平行而产生的,
5.相机标定的分类
传统的标定算法,
自标定法
基于主动视觉的标定法
标定流程:
- 打印一张棋盘格标定图纸,将其贴在平面物体的表面.
- 拍摄一组不同方向棋盘格的图片,可以通过移动相机来实现,也可以移动标定图片来实现。
-
对于每张拍摄的棋盘图片,检测图片中所有棋盘格的特征点。
-
因为棋盘标定图纸中所有角点的空间坐标是已知的,这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的,如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒),就可以根据LM等优化方法得到单应性矩阵H,得到相机的内参,外参等信息。
6.1. 棋盘格数据
6.2. 单应性矩阵
6.3. 利用约束条件求解内参矩阵
基于理想情况下的解,从几何推导上证明了张氏标定的可行性,并没有物理意义。在实际应用中,一般使用极大似然估计进行结果进行改善。
6.5. 极大似然参数估计
极大似然估计是一种估计总体未知参数的方法。它主要用于点估计问题。所谓点估计是指用一个估计量的观测值来估计未知参数的真值,即在参数空间中选取使得样本取得观测值的概率最大的参数。
径向畸变的前两个参数k1,k2
6.6.优化方法(CV常用)
如果要优化的问题为线性的可以直接对目标函数求导,并且令其等于零,以此求得其极值,并通过比较求取全局最小值(Global Minimizer),并将其最为目标函数的解。
如果问题为非线性,此时我们通常无法直接写出其导数形式(函数过于复杂),因此不去试图直接找到全局最小值,而是退而求其次通过不停的迭代计算寻找到函数的局部最小值(Local Minimizer),并认为该局部最小值能够使得我们的目标函数取得最优解(最小值),这就是非线性最小二乘的通常求解思路。很显然,在张氏较正中优化问题并不是线性的,我们需要通过迭代来求最优解。
6.6.1. 迭代方法
梯度下降法和牛顿法等等。
梯度下降,牛顿,高斯牛顿,LM等确定detx。
6.6.2. 牛顿法
牛顿法主要用来解决非线性优化问题,其收敛速度比梯度下降速度快。
6.6.3. 高斯牛顿法
高斯牛顿(Gauss-Newton)法是对牛顿法的一种改进,它用雅克比矩阵的乘积近似代替牛顿法中的二阶Hessian 矩阵,从而省略了求二阶Hessian 矩阵的计算。
高斯牛顿法虽然不用求Hessian矩阵,减小计算量,但是这个算法还是不完美。首先在牛顿法中,hessian矩阵是可逆的,而在高斯牛顿法中,用来近似Hessian矩阵的可能是奇异或病态的,会导致算法不收敛;另外,我们采用泰勒展开进行推导,泰勒展开只适合在较小范围内近似,如果步长较大,泰勒近似就不准确,也会导致算法不收敛。
6.6.4. LM法
Levenberg-Marquardt(LM)法在一定程度上修正了高斯牛顿法的缺点,因此它比高斯牛顿法更加鲁棒,不过这是以牺牲一定的收敛速度为代价的--它的收敛速度比高斯牛顿法慢。
其中,I是单位矩阵,μ是一个非负数。如果μ取值较大时,μI 占主要地位,此时的LM算法更接近一阶梯度下降法,说明此时距离最终解还比较远,用一阶近似更合适。反之,如果 μ取值较小时,H 占主要地位,说明此时距离最终解距离较近,用二阶近似模型比较合适,可以避免梯度下降的“震荡”,容易快速收敛到极值点。因此参数 μ不仅影响到迭代的方向还影响到迭代步长的大小。
其中,\tauτ 需手动指定,算法对\tauτ 不敏感,所以我们可以将其设为1。a_{ii}aii 表示矩阵A的对角线元素。
LM采用的搜索方法是信赖域(Trust Region)方法,因为高斯牛顿法中采用近似泰勒函数只在展开点附近有较好的近似效果,如果步长太大近似就不准确,
LM算法可以一定程度避免系数矩阵的非奇异和病态问题,可以提供更鲁棒、更准确的步长。因此LM算法在相机标定、视觉SLAM等领域中应用非常广泛。
6.7. 标定流程(重要)
张氏标定证明通过4组以上的点就可以求解出H矩阵的值,但是为了减少误差,具有更强的鲁棒性,我们一般会拍摄许多张照片,选取大量的角点进行标定。
- 打印一张棋盘格标定图纸,将其贴在平面物体的表面.
- 拍摄一组不同方向棋盘格的图片,可以通过移动相机来实现,也可以移动标定图片来实现。
- 对于每张拍摄的棋盘图片,检测图片中所有棋盘格的特征点(角点,也就是下图中黑白棋盘交叉点,中间品红色的圆圈内就是一个角点)。我们定义打印的棋盘图纸位于世界坐标系zw=0的平面上,世界坐标系的原点位于棋盘图纸的固定一角(比如下图中黄色点)。像素坐标系原点位于图片左上角。
- 因为棋盘标定图纸中所有角点的空间坐标是已知的,这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的,如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒),就可以根据LM等优化方法得到单应性矩阵H,进而得到相机的内参,外参等信息。
7. 双目标定(了解)
双目较正,就是利用单目校正得到每个相机的参数后,在计算两个相机之间的相对位置。