【剑指offer】最长不含重复字符的子字符串

学而不思则罔，思而不学则殆

---

题目

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。
假设字符串中只包含’a’-'z’的字符。例如：在字符串“arabcacfr”中，最长的不重复字符的子字符串是“acfr”,长度为4.

解法一 - 暴力解法O(n³)

首先第一眼我们能想到的算法，计算出所有的子字符串，然后计算这些子字符串中不包含重复字符且最长的子字符串，最终得出长度。该方法唯一的缺点就是效率，但是很好理解。
一个长度为n的字符串有**O(n²)个子字符串，需要O(n)**的时间判断一个子字符串是否包含重复的字符，因此该解法总的时间复杂度为$$O(n^3)$$

解法二 - 双循环O(n²)

记录两个left和right指针，right表示以i结束的不重复子字符串右边的位置。left表示以i结束的不重复子字符串左边的位置。因此此时不重复长度为[right - left + 1],并更新当前最长长度。整体时间复杂度为:$$O(n^2)$$

1. 第i个字符在[left，right]中没有出现，更新right，更新最大值
2. 第i个字符在[left，right]中没有出现，更新left,right，更新最大值

算法

    private static int solution2(String values) {
     
        if (values == null || values.length() == 0)
            return 0;
        if (values.length() == 1) {
     
            return 1;
        }
        int max = 1;
        int left = 0;//左指针
        int right = 0;//右指针
        for (int i = 1; i < values.length(); i++) {
     
            char ch = values.charAt(i);
            //判断ch字符有没有在[left,right]出现过
            int lastIndex = checkCh(values, left, right, ch);
            if (lastIndex == -1) {
     //没有出现过
                //更新右指针
                right = i;
            } else {
     //出现过。更新left指针
                left = lastIndex + 1;
                //更新右指针
                right = i;
            }

            //更新最大长度
            if (right - left + 1 > max) {
     
                max = right - left + 1;
            }
        }
        return max;
    }

    /**
     * 判断ch字符有没有在[left,right]出现，返回出现的位置
     *
     * @param values
     * @param left
     * @param right
     * @param ch
     * @return 出现过，返回位置，没有出现过，返回-1
     */
    private static int checkCh(String values, int left, int right, char ch) {
     
        for (int i = left; i <= right; i++) {
     
            if (ch == values.charAt(i)) {
     //字符出现过
                return i; //返回当前位置
            }
        }
        return -1; //没有出现过。返回-1
    }

测试

        String values = "arabcacfrn";
        int max = solution2(values);
        System.out.println(values + " max:" + max);

        values = "";
        max = solution2(values);
        System.out.println(values + " max:" + max);

        values = null;
        max = solution2(values);
        System.out.println(values + " max:" + max);


        values = "null";
        max = solution2(values);
        System.out.println(values + " max:" + max);


        values = "aaaaaaaaaaaaaaaaaaaaaaaaa";
        max = solution2(values);
        System.out.println(values + " max:" + max);


        values = "aaaaaaaaaaaaaabaaaaaaaaaaa";
        max = solution2(values);
        System.out.println(values + " max:" + max);

测试结果

arabcacfrn max:5
 max:0
null max:0
null max:3
aaaaaaaaaaaaaaaaaaaaaaaaa max:1
aaaaaaaaaaaaaabaaaaaaaaaaa max:2

解法三-滑动窗口 O(n)

整体思路，维护一个窗口：

窗口右边指向当前位置
窗口左边指向以当前位置为结尾的不重复子字符串的初始位置

此时滑动窗口的left=1,right = 2，那么此时的长度为d = rigit - left +1 = 2

当坐标i= 5的时候，此时窗口的left= 3,right = 5, 此时长度为 d = right - left +1 = 3

算法思路

$$f(窗口更新)=\{\begin{array}{ll}窗口左边界不动，右边界指向当前位置& \text{arr[i]字符没有出现过}\\ arr[i]字符出现过=\{\begin{array}{ll}收缩窗口左边界，右边界指向当前位置& \text{字符在窗口内}\\ 窗口左边界不动，右边界指向当前位置& \text{字符在串口外}\end{array}& \end{array}$$

整体来说一次循环就可找到结果，时间复杂度为:
$$O(n)$$

简单实例讲解

以【rsthtfkffx】为例，这个结果是：4 【rsth】或者【htfk】

1.第0位，字符为r

序号	字符	图形	左边界	右边界	结果	图形
0	r		0	0	1
1	s		0	1	2
2	t		0	2	3
3	h		0	3	4
4	t		3	4	2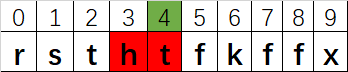
5	f		3	5	2
6	k		3	6	4
7	f		6	7	2
8	f		8	8	1
9	x		8	9	2

最终结果就是：4

算法代码

    //解法三 时间复杂度为O(n) - 滑动窗口
    private static int solution3(String values) {
     
        if (values == null || values.length() == 0)
            return 0;
        if (values.length() == 1) {
     
            return 1;
        }
        int max = 0;
        int[] flag = new int[256];
        //默认为-1 ，表示该字符没有出现过，否则表示该字符出现在上一个位置下标
        Arrays.fill(flag, -1);
        int left = 0;
        int right = 0;
        max = 1;
        flag[values.charAt(0)] = 0;

        //从1开始
        for (int i = 1; i < values.length(); i++) {
     
            char ch = values.charAt(i);
            int lastIndex = flag[ch];
            flag[ch] = i; //记录字符最新出现的位置下标
            if (lastIndex == -1) {
     //没有出现过
            } else {
     //出现过
                if (lastIndex >= left) {
     
                    left = lastIndex + 1;
                }
            }
            right = i;
            //更新最新的值
            if (max < right - left + 1) {
     
                max = right - left + 1;
            }
        }
        return max;
    }

简单测试

testSolution3--------------------
arabcacfrn max:5
 max:0
null max:0
null max:3
aaaaaaaaaaaaaaaaaaaaaaaaa max:1
aaaaaaaaaaaaaabaaaaaaaaaaa max:2

解法四-动态规划 O(n)

首先定义函数:
f(x) 表示以第 i个字符为结尾的不包含重复字符的子字符串的最长长度。

我们从左到右逐一扫描字符串中的每一个字符。当我们计算以第i个字符为结尾的不包含重复字符的子字符串的最长长度f(i)时，我们已经知道f(i-1)了。

---

情况一：如果第i个字符之前没有出现过，那么f(i) = f(i-1)+1。例如。在字符"abasrfasd"中，显然f(0) = 1。在计算f(1)时，下标为1的字符‘b’之前没有出现过，因此f(1) = 2 ,即f(1) = f(0) + 1.到目前为止，最长的不含重复字符的子字符串是"ab".
情况二： 如果第i个字符之前已经出现过，那么情况就要复杂一点了。我们计算第i个字符和他上一次出现的位置的距离，并记为d,接着分为两种情况分析:

第一种：d <= f(i-1),此时第i个字符上次出现在f(i-1)对应的最长子字符串中，因此f(i) = d.同时也以为着在第i个字符出现两次所夹的子字符串中再也没有其他重复的字符了。
第二种：d> f(f-1)，此时第i字符上次出现在f(i-1)对应的最长子字符串之前，因此仍然有f(i) = f(i-1) +1 .

算法思路

$$f(i)=\{\begin{array}{ll}f(i-1)+1& \text{第i个字符没有出现过}\\ 第i个字符出现过=\{\begin{array}{ll}d& \text{d <= f(i-1)}\\ f(i-1)+1& \text{d>f(i-1)}\end{array}& \end{array}$$

我们计算第i个字符和他上一次出现的位置的距离，并记为d

整体来说一次循环就可找到结果，时间复杂度为:
$$O(n)$$

简单实例讲解

以"arabcafr"为例

序号	当前字符	字符上次出现的位置	与上次出现的距离d	比较	f(i)
0	a	-1	-	-	1
1	r	-1	-	-	f(1)= f(0)+1 = 2
2	a	0	2	d<= f(1)	f(2) = d = 2
3	b	-1	-	-	f(3) = f(2)+1 = 3
4	c	-1	-	-	f(4)= f(3)+1 = 4
5	a	2	3	d<= f(4)	f(5) = d = 3
6	f	-1	-	-	f(6) = f(5)+1 = 4
7	r	1	6	d>f(6)	f(7) = f(6)+1 = 5

所以最终结果是:5

算法范例

    //解法三 时间复杂度为O(n) - 动态规划
    private static int solution4(String values) {
     
        if (values == null || values.length() == 0)
            return 0;
        if (values.length() == 1) {
     
            return 1;
        }
        int max = 0;
        int[] flag = new int[256];
        int[] result = new int[values.length()];
        //默认为-1 ，表示该字符没有出现过，否则表示该字符出现在上一个位置下标
        Arrays.fill(flag, -1);
        //初始化第0位
        max = 1;
        flag[values.charAt(0)] = 0;
        result[0] = 1;

        //从1开始
        for (int i = 1; i < values.length(); i++) {
     
            char ch = values.charAt(i);
            int lastIndex = flag[ch];
            flag[ch] = i; //记录字符最新出现的位置下标
            if (lastIndex == -1) {
     //没有出现过
                result[i] = result[i - 1] + 1;
            } else {
     //出现过
                int d = i - lastIndex;
                if (d > result[i - 1]) {
     
                    result[i] = result[i - 1] + 1;
                } else {
     
                    result[i] = d;
                }
            }
            //更新最新的值
            if (max < result[i]) {
     
                max = result[i];
            }
        }
        return max;
    }

简单测试

arabcacfrn max:5
 max:0
null max:0
'null' max:3
aaaaaaaaaaaaaaaaaaaaaaaaa max:1
aaaaaaaaaaaaaabaaaaaaaaaaa max:2