通学智能合约系列（五）--整型溢出

3.整型溢出及异常处理

在上节中，如果你认真去码了一遍运算案例，可能小伙伴已经感觉到了隐隐的不安，因为这种算术操作，一旦超出所占位数后，就会变的不可控。所以我们要了错于心，防患于未然。

要掌控的溢出

下面我们来看一个例子:

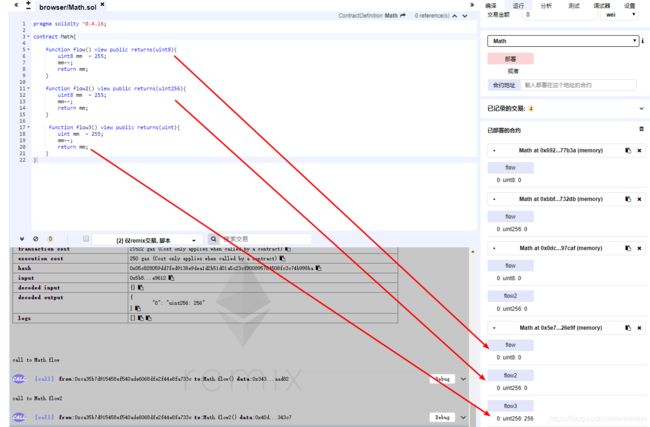
pragma solidity ^0.4.16;

contract Math{
     
    
    function flow() view public returns(uint8){
     
        uint8 mm  = 255;
        mm++;
        return mm;
    }
    
    function flow2() view public returns(uint256){
     
        uint8 mm  = 255;
        mm++;
        return mm;
    }
    
     function flow3() view public returns(uint){
     
        uint mm  = 255;
        mm++;
        return mm;
    }
}

执行结果后，我们发现调用flow=0，flow2=0， flow3=256 .这里我没有按照原视频中的例子，而是自己综合比较了uint8 与uint的区别 以及++复合操作。相信大家都直接这个结果是什么原因造成的。那就是进位溢出导致。

我们在来看看复合减的运算：

pragma solidity ^0.4.16;

contract Math{
     
    
    function flowMinus() view returns(uint8){
     
        uint8 nn = 0;
        nn--;
        return nn;
    }
    
    function flowMinus2() view returns(uint8){
     
        uint8 nn = 0;
        nn--;
        return nn--;
    }
    
    function flowMinus3() view returns(uint8){
     
        uint8 nn = 0;
        return nn--;
    }
}

大家可以先看看这个代码，猜猜答案分别是什么？然后在动手验证一下。

这里为了帮助大家更好地理解溢出，我用excel简单地描述了下，可以看一看。

最后，我们来揭晓答案：上述的复合减运算答案分别是255,255和0.如果你没有一次性答对的话，不要灰心，看看我之前分享后口诀。再多码两遍，多思考下，相信你一定可以搞懂。如果还是搞不懂，关注我，加我微信吧 ，手把手教会你（虽然知道这里都是有经验的开发人员，但或许也有喜欢学习的初学者哦）。

要避免的异常

我们在学其他语言的时候，都知道除以0是会有问题的，也知道小数类型精度丢失是很麻烦的。在智能合约的时候里，也不例外，我们一起来看看吧

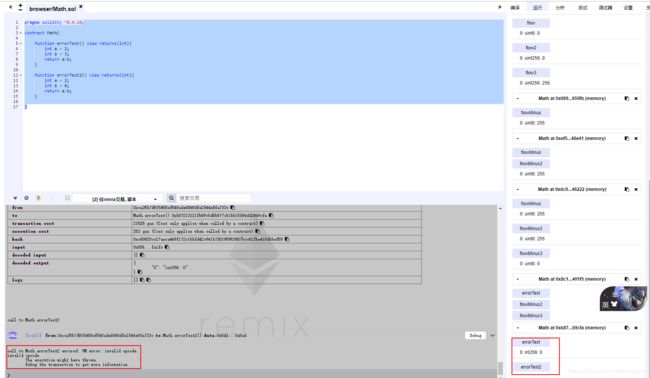
pragma solidity ^0.4.16;

contract Math{
     
    
    function errorTest() view returns(int){
     
        int a = 2;
        int b = 3;
        return a/b;
    }
    
    function errorTest2() view returns(int){
     
        int a = 2;
        int b = 0;
        return a/b;
    }
    
}

执行结果，我们可以发现，第一个返回是0.答案显然也是不能让我们满意的。而第二个则直接抛出错误。 看来不能除零已经是公理了。

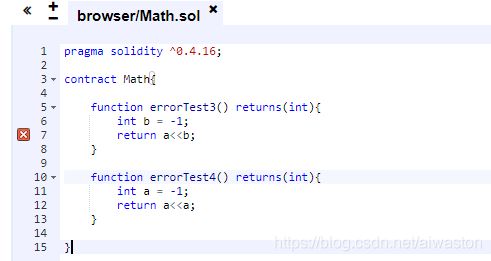
另外，我们再来看看其他的异常。

显然，errorTest3没有能逃过编译器，而errorTest4虽然逃过了编译器的法眼，也成功部署了，但执行肯定还是会报错的。

上面这些异常大家在写合约的时候，要注意哦，如果你还遇到了其他异常，可以拿来，一起分享。

4.整型字面量

emmm，虽然接触了变成也有好几年的时候了，但是好像平常都不怎么说字面量，那么字面量到底是什么。百度百科是这么说的。

在计算机科学中，字面量（literal）是用于表达源代码中一个固定值的表示法（notation）。几乎所有计算机编程语言都具有对基本值的字面量表示，诸如：整数、浮点数以及字符串；而有很多也对布尔类型和字符类型的值也支持字面量表示；还有一些甚至对枚举类型的元素以及像数组、记录和对象等复合类型的值也支持字面量表示法.

这里看了知乎上的一些案例： https://www.zhihu.com/question/62411257

说白了，就是表示数字或者字符的一种形式。例如我们常常定义的int a = 1;就可以说1是a的字面量。可以直接表征不确定性事物的一种特定直观的量值。

这里我们主要是看看solidity中整型在执行一些非常规形式运算时可以自动收敛的情况。例如:

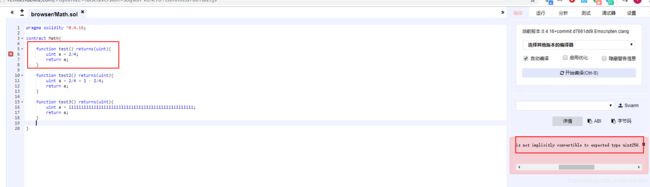
pragma solidity ^0.4.16;

contract Math{
     
    
    function test1() returns(uint){
     
        uint  a = 2/4;
        return a;
    }

    function test2() returns(uint){
     
        uint a = 2/4 + 1 - 2/4;
        return a;
    }
    
    function test3() returns(uint8){
     
        uint8 a = 11111111111111111111112 - 11111111111111111111111;
        return a;
    }
    
}

这里第一个例子，因为uint256无法表示一个小数，所以没有办法收敛。而下面两个例子，他们的最终结果是确定性的，所以可以编译通过。直接结果后，我们发现两者结果都是确定值1.

也就是说：等号后面的字面量可以表征前面的确定值。

在这里，整型部分我们就说完了。接下来，到我们的重点 数组。