深度强化学习简述
深度强化学习简述
0 写在前面
主要参考《A Brief Survey of Deep Reinforcement Learning》
1 引言
如今广泛意义上的机器学习既包括传统的偏向数理统计方面的机器学习,也包含基于神经网络的深度学习,也有基于奖励机制的半监督式机器学习,即强化学习,它是一类特殊的机器学习算法,借鉴于行为主义心理学,特别适用于智能体或者机器人的控制与决策问题,它要解决的问题是在环境中怎样执行动作以获得最大的累计奖励,例如例如,对于自动行驶的汽车,强化学习算法控制汽车的动作,保证安全行驶到目的地。对于围棋算法,算法要根据当前的棋局来决定如何走子,以赢得这局棋,著名的AlphaGo就是强化学习产出的棋手。然而,传统无模型强化学习方法需要使用函数逼近技术使得主体能够学习出值函数或者策略。在这种情况下,深度学习强大的函数逼近能力自然成为了替代人工指定特征的最好手段并为性能更好的端到端学习的实现提供了可能,于是深度强化学习应运而生,例如将传统强化学习QLearning算法中的状态-动作表通过深度学习的方法预测得出就出现了DQN。从这个角度上,换句话说深度强化学习能够处理更高维的状态-动作空间。
深度强化学习(DRL)的应用范围比较广泛,不止是在Go[1]和打星际争霸等策略游戏领域,近年DeepMind团队在导航上面的进展[2]也是用的DRL方法,另外一些领域诸如自然语言处理和博弈论等等,一些新兴的前沿领域如多智能体等。
2 强化学习
在讲到DRL之前有必要先简介强化学习,如下
2.1 马尔可夫决策过程
在数学上,RL可被描述为为马尔可夫决策过程(MDP),包含:
-
一个状态集 S S S ,和起始状态分布 p ( s 0 ) p\left(\mathbf{s}_{0}\right) p(s0)
-
动作集 A \mathcal{A} A
-
一个过渡动态(Transition dynamics) T ( S t + 1 ∣ S t , a t ) \mathcal{T}\left(\mathbf{S}_{t+1} | \mathbf{S}_{t}, \mathbf{a}_{t}\right) T(St+1∣St,at),用来描述每个动作对当前状态的影响,
-
一个即时奖励函数 R ( s t , a t , s t + 1 ) \mathcal{R}\left(\mathbf{s}_{t}, \mathbf{a}_{t}, \mathbf{s}_{t+1}\right) R(st,at,st+1)
-
一个衰减因子 γ ∈ [ 0 , 1 ] \gamma \in[0,1] γ∈[0,1],作用于稀疏奖励
一般地,定义策略 π : S → p ( A = a ∣ S ) \pi: \mathcal{S} \rightarrow p(\mathcal{A}=\mathbf{a} | \mathcal{S}) π:S→p(A=a∣S)为从状态到动作概率分布的映射,如果MDP是回合制的(episodic),那么在每个回合长度 T T T之后,状态会重置,然后该回合中的状态,行为和奖励序列组成一个策略的轨迹(trajectory or rollout)。每个策略轨迹下累积奖励为回报(return) R = ∑ t = 0 T − 1 γ t r t + 1 R=\sum_{t=0}^{T-1} \gamma^{t} r_{t+1} R=∑t=0T−1γtrt+1。RL的目标就是找出一个最优策略 π ∗ \pi^{*} π∗使得最终的回报最大:
π ∗ = argmax π E [ R ∣ π ] \pi^{*}=\underset{\pi}{\operatorname{argmax}} \mathbb{E}[R | \pi] π∗=πargmaxE[R∣π]
MDP一个关键属性就是只有当前状态影响下一个状态,即当前时刻 s t \mathbf{s}_{t} st只依赖于前一个时刻 S t − 1 \mathbf{S}_{t-1} St−1 而不是 { s 0 , s 1 , … , s t − 1 } \left\{\mathbf{s}_{0}, \mathbf{s}_{1}, \dots, \mathbf{s}_{t-1}\right\} { s0,s1,…,st−1}。尽管这是主流RL中的常见假设,但是这有点不切实际,因为它要求所有状态可观测(fully observable)。而MDP的一个泛化是部分可观测的MDP(POMDP, partially observable MDPs),在POMDP中智能体接受一个观测(observation) o t ∈ Ω \mathbf{o}_{t} \in \Omega ot∈Ω,该分布 p ( o t + 1 ∣ s t + 1 , a t ) p\left(\mathbf{o}_{t+1} | \mathbf{s}_{t+1}, \mathbf{a}_{t}\right) p(ot+1∣st+1,at)独立于当前状态和之前的动作[3]。在给定前一个可信状态、采取的动作和现在的观测值下,POMDP算法一般会对现有状态保持一个信任(belief),即一般不改变当前状态。在深度学习中,一个更通用的方法就是采取RNN[4,5,6],它不像前馈神经网络而是一个动态系统。这种解决POMDP的方法与使用动力学系统和状态空间模型的其他问题有关,在这些问题中,只能估计真实状态[7]。
2.2 RL面临的一些挑战
RL目前面临的一些挑战如下:
- 最优化策略必须通过在环境中的反复试错推断得出,智能体唯一能接收到的信号就是奖励
- 对智能体的观测依赖于它的行为action,并且很可能有很强的时间相关性
- 智能体必须处理长时间的依赖关系:通常,行为的后果只有在环境发生许多变化后才会实现。,这称为(时间)信用分配问题(credit assignment problem)[8]
2.3 RL算法
RL算法主要分为三大类,基于值函数和基于策略搜索的(policy search),还有就是两者的结合,即actor-critic方法。
2.3.1 值函数
值函数是通过给定一个状态估计对应的值或者说期望的回报的方法,用状态-值函数 V π ( s ) V^{\pi}(\mathbf{s}) Vπ(s) 表示在起始状态为 s s s策略为 π \pi π下的期望回报:
V π ( s ) = E [ R ∣ s , π ] V^{\pi}(\mathbf{s})=\mathbb{E}[R | \mathbf{s}, \pi] Vπ(s)=E[R∣s,π]
相应的最优策略 π ∗ \pi^{*} π∗对应的最优状态-值函数为:
V ∗ ( s ) = max π V π ( s ) ∀ s ∈ S V^{*}(\mathbf{s})=\max _{\pi} V^{\pi}(\mathbf{s}) \quad \forall \mathbf{s} \in \mathcal{S} V∗(s)=πmaxVπ(s)∀s∈S
如果 V ∗ ( s ) V^{*}(\mathbf{s}) V∗(s)可变,那么最优化策略可以以下方式检索得到,即通过选择状态 S t \boldsymbol{S}_{t} St下所有可得到的行为并且选择其中能使得期望值 E S t + 1 ∼ T ( s t + 1 ∣ s t , a ) [ V ∗ ( S t + 1 ) ] \mathbb{E}_{\mathbf{S}_{t+1 \sim \mathcal{T}}(\mathbf{s}_{t+1} | \mathbf{s}_{t}, \mathbf{a})}\left[V^{*}\left(\mathbf{S}_{t+1}\right)\right] ESt+1∼T(st+1∣st,a)[V∗(St+1)]最大的行为。
在RL设定中,这个转变动态(transition dynamics) T \mathcal{T} T无法得到。但是可以建立其它的函数,即状态-行为函数或者质量函数 Q π ( s , a ) Q^{\pi}(\mathbf{s}, \mathbf{a}) Qπ(s,a),这跟状态-值函数 V π ( s ) V^{\pi}(\mathbf{s}) Vπ(s) 相似,其区别就是状态-行为函数知道初始行为或者动作的:
Q π ( s , a ) = E [ R ∣ s , a , π ] Q^{\pi}(\mathbf{s}, \mathbf{a})=\mathbb{E}[R | \mathbf{s}, \mathbf{a}, \pi] Qπ(s,a)=E[R∣s,a,π]
那么最佳策略可以通过使得每个状态的 Q π ( s , a ) Q^{\pi}(\mathbf{s}, \mathbf{a}) Qπ(s,a)最大得到,即 argmax a Q π ( s , a ) \operatorname{argmax}_{\mathbf{a}} Q^{\pi}(\mathbf{s}, \mathbf{a}) argmaxaQπ(s,a)。
在实际学习最佳策略 Q π Q^{\pi} Qπ的过程中,首先利用马尔可夫性质定义函数为一个贝尔曼等式[9],即以下形式,注意 π ( s t + 1 ) = a t + 1 \pi\left(\mathbf{s}_{t+1}\right)=a_{t+1} π(st+1)=at+1:
Q π ( s t , a t ) = E s t + 1 [ r t + 1 + γ Q π ( s t + 1 , π ( s t + 1 ) ) ] Q^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)=\mathbb{E}_{\mathbf{s}_{t+1}}\left[r_{t+1}+\gamma Q^{\pi}\left(\mathbf{s}_{t+1}, \pi\left(\mathbf{s}_{t+1}\right)\right)\right] Qπ(st,at)=Est+1[rt+1+γQπ(st+1,π(st+1))]
这意味着 Q π Q^{\pi} Qπ能够通过bootstrapping算法来改善,可以使用当前的估计值来改善估计。以下是Q-learning[10]和state-action-reward-state-action (SARSA)算法[11]的基础:
Q π ( s t , a t ) ← Q π ( s t , a t ) + α δ Q^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \leftarrow Q^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\alpha \delta Qπ(st,at)←Qπ(st,at)+αδ
其中 α \alpha α是学习率, δ = Y − Q π ( s t , a t ) \delta=Y-Q^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) δ=Y−Qπ(st,at)是时间差分误差(temporal difference (TD) error), Y Y Y是一个标准回归问题的目标,在Q-learning中, Y = r t + γ max a Q π ( s t + 1 , a ) Y=r_{t}+\gamma \max _{\mathbf{a}} Q^{\pi}\left(\mathbf{s}_{t+1}, \mathbf{a}\right) Y=rt+γmaxaQπ(st+1,a),这里SARSA跟Q-learning的区别在于前者是基于在线策略,后者是离线策略,具体不展开。
2.3.2 策略搜索(policy)
策略搜索方法不需要维持值函数模型,而是直接搜索最佳策略 π ∗ \pi^{*} π∗。通常选择一个参数化的策略 π θ \pi_{\theta} πθ,其参数可以通过基于梯度的或无梯度的优化方法[12]更新来使得期望回报 E [ R ∣ θ ] \mathbb{E}[R | \theta] E[R∣θ]最大。无梯度优化通常在低维参数空间下有效,基于梯度的训练更多地应用于深度强化学习算法,相应的参数也会更多。
直接构建策略时,通常会输出参数的概率分布。 对于连续动作,这可能是高斯分布的均值和标准差,而对于离散动作,这可能是多项式分布的各个概率。 结果就是一种随机策略,可以从中直接采样动作(action)。 使用无梯度方法,要找到更好的策略,就需要在预定义的模型类别中进行启发式搜索。 诸如进化策略之类的方法,实质上是在策略的子空间中使用爬山方法[13],而诸如压缩网络搜索之类的更复杂的方法则施加了额外的归纳偏差[14]。 无梯度策略搜索的最大优势也许在于它们还可以优化不可区分的策略。
Policy Gradients:梯度可以为如何改进参数化策略提供强大的学习信号。但是,要计算预期回报,需要对当前政策参数化所引发的轨迹进行平均。这种平均需要确定性逼近(例如线性化)或通过采样的随机逼近。确定性近似只能应用于基于模型的环境中,在该环境中转变动态(transition dynamics) T \mathcal{T} T可知。但是在更常见的无模型RL中,通常使用蒙特卡洛估计预期回报。对于基于梯度的学习,由于梯度无法通过随机函数的这些样本,因此这种蒙特卡洛逼近法带来了挑战。因而在RL中常用称为REINFORCE规则(也是最基本常用的规则)[15]的梯度估计器,或者其他方法如得分函数[16]或似然比估计器[17]。REINFORCE规则可以用于计算相对于参数 θ \theta θ的随机变量 X X X的函数 f f f的期望梯度:
∇ θ E X [ f ( X ; θ ) ] = E X [ f ( X ; θ ) ∇ θ log p ( X ) ] \nabla_{\theta} \mathbb{E}_{X}[f(X ; \theta)]=\mathbb{E}_{X}\left[f(X ; \theta) \nabla_{\theta} \log p(X)\right] ∇θEX[f(X;θ)]=EX[f(X;θ)∇θlogp(X)]
但是该计算方式依赖于轨迹的期望回报,这导致梯度具有较高的方差,可以引入噪声较小的无偏估计来减小。
2.3.3 Actor-Critic方法
该方法是值函数和基于策略搜索的结合方法,如下图
“actor”(即策略)通过来自"critic"(即值函数)的反馈来学习,这种方式权衡了policy gradient带来的方差和值函数引入的偏差,方差偏差的权衡也是统计学习理论的一个重要内容。
2.4 DRL的出现
深度神经网络的引入使RL能够处理一些高维问题。通过表征学习(representation learning),DRL可以有效地处理维数诅咒问题,这与传统表格化的非参数方法不同。 例如,卷积神经网络(CNN)可以用作RL代理的组成部分,从而使他们可以直接从原始的高维视觉输入中学习。通常,DRL是基于深度神经网络的训练来近似最优策略 π ∗ \pi^{*} π∗,或者最优值函数 V ∗ , Q ∗ V^{*}, Q^{*} V∗,Q∗。
尽管目前也有基于无梯度的DRL方法[18],但目前主流还是依赖于梯度和反向传播算法,原因是如果梯度可得就能提供一个强大的学习信号。实际中这些梯度一般通过采样或者其他的方法近似估计得到。反向传播的一个好处就是能将期望回报的优化看作是一个随机函数的优化。
3 DRL算法
3.1 值函数
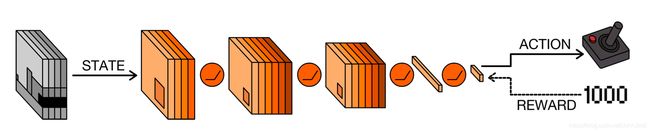
基于值函数的方法比较典型的是DQN,DQN[19]是基于Q-learning的改进,在处理高维问题时,Q-learning需要庞大的Q表作支撑,但是目前的存储条件有限,而DQN中可以利用深度网络来对Q值作较为精准的估计,这个估计也叫函数逼近(function approximaion)。如下图该结构能够在经典的Atari 2600游戏中取得与资深玩家相媲美的分数。
DQN的输入是游戏的四个灰度帧,它们随时间而级联,最初由几个卷积层处理,以提取时空特征,例如球在“Pong”或“Breakout”游戏中的运动。卷积层的最终特征图由几个完全连接的层处理,这些层更隐式地编码动作的效果。 这与使用固定预处理步骤的传统控制器形成对比,传统控制器无法响应于学习信号来调整其状态处理。
DQN通过使用两种技术解决了在RL [145]中使用函数逼近的基本不稳定性问题:经验回放(experience replay)和目标网络。经验回放将transition以 ( s t , a t , s t + 1 , r t + 1 ) \left(\mathbf{s}_{t}, \mathbf{a}_{t}, \mathbf{s}_{t+1}, r_{t+1}\right) (st,at,st+1,rt+1)的形式存储在一个循环缓冲区中,是RL智能体能够可以从先前的观测数据中进行采样并进行离线训练。
这不仅极大地减少了与环境的交互,而且可以提取大量的经验,从而减少了学习更新的差异。 此外,通过从大内存中均匀采样,可以破坏对RL算法产生不利影响的时间相关性。 最后,从实际角度出发,现代硬件可以有效地并行处理一批数据,从而提高吞吐量。 虽然最初的DQN算法使用均匀采样[19],但后来的工作表明,基于TD误差对样本进行优先级排序对于学习更为有效。 尽管经验回放通常被认为是一种无模型的技术,但实际上它可以被认为是一种简单的模型[20]。
第二种方法目标网络由Mnih等人提出[19],该目标网络最初包含制定策略的网络权重,但长时间保持冻结状态。策略网络使用固定的目标网络,而不必根据自身对Q值的快速波动估计来计算TD误差。 在训练过程中,目标网络的权重将在固定数量的步骤后更新为与策略网络匹配的值。
3.2 策略搜索
3.2.1 随机函数的反向传播
目前DRL的主流方式仍然是反向传播[21]。先前讨论的REINFORCE规则允许神经网络以任务相关的方式(task- dependent manner,)学习随机策略,例如决策从何处寻找图片进行追踪,分类或理解对象(image caption objects)。在这些情况下,随机变量将确定一小幅的坐标,从而减少所需的计算量。一般而言,使用REINFORCE 或“重新参数化技巧(reparameterisation trick)” 等技术进行随机函数反向传播,允许将神经网络视为随机计算图(stochastic computation graphs)[22],这也是诸如随机值梯度(SVG)等算法中的关键概念。
3.2.2 复合误差(Compounding Errors)
直接搜索由具有很多参数的神经网络表示的策略可能很困难,并且可能会面临严重的局部最小值问题。 解决此问题的一种方法是使用引导策略搜索(GPS),该策略从其他控制器(可以使用分离的方法separate method构造,如最优控制)获取一些动作序列。GPS通过结合有监督的学习和重要性采样(importance sampling)从中学习,从而纠正一些离线策略样本(off-policy samples),这种方法能有效地使搜索偏向一个好的(局部)最优值。 GPS通过优化策略以匹配采样轨迹,并优化轨迹分布以匹配策略并最小化成本,从而实现了循环工作。 最初,GPS用于模拟连续的RL问题的神经网络训练[23],但后来被用来训练基于视觉输入的真实机器人的策略[24]。 Levine等人的这项研究[24]表明,有可能实现“端到端(end-to-end)”的机器人训练视觉运动策略,直接从相机的RGB像素到电机扭矩,这是DRL中的开创性工作之一。
一种更常用的方法是使用置信区域(trust regions),即优化步骤被限制为位于仍然保留真实成本函数近似值的区域内。通过防止更新的策略与之前的策略有太大的偏差,可以减少灾难性错误更新的可能性,并且许多使用置信区域的算法可以保证或实际上导致策略性能的单调提高。按照当前策略与拟议策略之间的Kullback-Leibler(KL)差异来衡量,约束每个策略梯度更新的想法在RL中已有很长的历史。基于该工作的一种较新算法,即置信区域策略优化(TRPO),已被证明是相对鲁棒的,且适用于高维输入的情况[25]。TRPO优化了替代目标函数(surrogate objective function),具体而言,它优化了(重要性采样)优势估计,并使用KL(Kullback-Leibler)散度的二次近似进行了约束。虽然TRPO可以用作具有简单基线(baseline)的纯策略梯度(policy gradient)方法,但是之后Schulma等人引入了广义优势估计(generalised advantage estimation,GAE),提出了一个更高级的方差减少基准(baseline),也可以将TRPO和GAE两者结合起来。然而TRPO的约束优化需要计算二阶梯度,从而限制了其适用性。而较新的近端策略优化(proximal policy optimisation, PPO)算法执行无约束的优化,只需要一阶梯度信息[26]。这两个主要变体包括对KL散度的适应性惩罚和与KL散度无关的启发式限幅目标[26]。 在保持TRPO性能的同时降低成本使得PPO(带有或不带有GAE)在RL任务中都越来越流行[26]。
3.3 Actor-Critic
前面RL讲到该方法是基于值函数和策略搜索两者的结合,因此在DRL当policy gradient可以用GAE优化以及基于值函数可以用目标网络改善时,那么在DRL中Actor-Critic同样也能获益。
Actor-Critic方面较新的进展是deterministic policy gradients(DPGs)[27],它将随机策略的标准策略梯度定理[28]扩展到确定性策略。DPG的主要优点之一是,尽管随机策略梯度在状态空间和动作空间上都可以集成,但DPG可仅在状态空间上进行集成,在较大动作空间中只需要较少样本。在DPG的初期工作中,Silver等人[27]引入并证明了一种off-policy Actor-Critic算法,该算法极大地改进了高维连续控制问题中的随机策略梯度。 后来的引入绍了深度DPG(DDPG),它利用神经网络在高维视觉状态空间上运行。最近Gu等人[29]将之前的方法统一在插值策略梯度(IPG)下,提出了一种最新的连续DRL算法,IPG和SVG(随机值梯度),其背后的思想共同构成了提高DRL中学习效率的算法方法,其中DPG可以认为是一种特例。
4 目前的主要研究
目前DRL主要集中无模型(model-free)的方法,而基于模型的RL算法在提高RL数据效率以及权衡探索(exploration)和开发(exploitation)方面发挥着重要作用。分层强化学习(Hierarchical RL)问题也是研究的重点之一,它通过将最终政策明确分解为几个层级,对最终策略施加归纳性偏置。此外鉴于来自其他一些控制器的轨迹可用于引导学习过程,因此也有模仿学习和逆RL(IRL)相关研究,然后就是研究多智能体系统方面[30]。 在DRL的背景下,其中也有两个更广泛的领域,即与RNN的结合[31]和迁移学习。
5 参考文献
[1]David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Lau- rent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature, 529(7587):484–489, 2016.
[2]Learning to Navigate in Cities Without a Map
[3]Leslie P Kaelbling, Michael L Littman, and Anthony R Cassandra. Planning and Acting in Partially Observable Stochastic Domains. Artificial Intelligence, 101(1):99–134, 1998.
[4] Daan Wierstra, Alexander Fo ̈rster, Jan Peters, and Ju ̈rgen Schmidhuber. Recurrent Policy Gradients. Logic Journal of the IGPL, 18(5):620–634, 2010.
[5]Matthew Hausknecht and Peter Stone. Deep Recurrent Q-Learning for Partially Observable MDPs. In AAAI Fall Symposium Series, 2015.
[6] Nicolas Heess, Jonathan J Hunt, Timothy P Lillicrap, and David Silver. Memory-Based Control with Recurrent Neural Networks. In NIPS Workshop on Deep Reinforcement Learning, 2015.
[7] Dimitri P Bertsekas. Dynamic Programming and Suboptimal Control: A Survey from ADP to MPC. European Journal of Control, 11(4-5): 310–334, 2005.
[8] Richard S Sutton and Andrew G Barto. Reinforcement Learning: An Introduction. MIT Press, 1998.
[9] Richard Bellman. On the Theory of Dynamic Programming. PNAS, 38(8):716–719, 1952.
[10] Christopher JCH Watkins and Peter Dayan. Q-Learning. Machine Learning, 8(3-4):279–292, 1992.
[11] Gavin A Rummery and Mahesan Niranjan. On-line Q-learning using Connectionist Systems. University of Cambridge, Department of Engineering, 1994.
[12] Marc P Deisenroth, Gerhard Neumann, and Jan Peters. A Survey on Policy Search for Robotics. Foundations and Trends⃝R in Robotics, 2 (1–2), 2013.
[13] Tim Salimans, Jonathan Ho, Xi Chen, and Ilya Sutskever. Evolu- tion Strategies as a Scalable Alternative to Reinforcement Learning. arXiv:1703.03864, 2017.
[14] Jan Koutn ́ık, Giuseppe Cuccu, Ju ̈rgen Schmidhuber, and Faustino Gomez. Evolving Large-Scale Neural Networks for Vision-Based Reinforcement Learning. In GECCO, 2013.
[15] Ronald J Williams. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Machine Learning, 8(3-4): 229–256, 1992.
[16] Michael C Fu. Gradient Estimation. Handbooks in Operations Research and Management Science, 13:575–616, 2006.
[17] Marta Garnelo, Kai Arulkumaran, and Murray Shanahan. Towards Deep Symbolic Reinforcement Learning. In NIPS Workshop on Deep Reinforcement Learning, 2016.
[18] Faustino Gomez and Ju ̈rgen Schmidhuber. Evolving Modular Fast- Weight Networks for Control. In ICANN, 2005.
[19] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. Human-Level Control through Deep Reinforcement Learning. Nature, 518(7540):529–533, 2015.
[20] Harm Vanseijen and Rich Sutton. A Deeper Look at Planning as Learning from Replay. In ICML, 2015.
[21] Paul John Werbos. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Technical report, Harvard University, Applied Mathematics, 1974.
[22] John Schulman, Nicolas Heess, Theophane Weber, and Pieter Abbeel. Gradient Estimation using Stochastic Computation Graphs. In NIPS, 2015.
[23] Sergey Levine and Pieter Abbeel. Learning Neural Network Policieswith Guided Policy Search under Unknown Dynamics. In NIPS, 2014
[24] Sergey Levine, Chelsea Finn, Trevor Darrell, and Pieter Abbeel. End-to-End Training of Deep Visuomotor Policies. JMLR, 17(39):1–40,2016.
[25] John Schulman, Sergey Levine, Pieter Abbeel, Michael Jordan, and Philipp Moritz. Trust Region Policy Optimization. In ICML, 2015.
[26] John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. Proximal Policy Optimization Algorithms. arXiv:1707.06347, 2017.
[27] David Silver, Guy Lever, Nicolas Heess, Thomas Degris, Daan Wier- stra, and Martin Riedmiller. Deterministic Policy Gradient Algorithms. In ICML, 2014.
[28] Ronald J Williams. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Machine Learning, 8(3-4): 229–256, 1992.
[29] Shixiang Gu, Timothy Lillicrap, Zoubin Ghahramani, Richard E Turner, Bernhard Scho ̈lkopf, and Sergey Levine. Interpolated Policy Gradient: Merging On-Policy and Off-Policy Gradient Estimation for Deep Reinforcement Learning. In NIPS, 2017.
[30] Johannes Heinrich and David Silver. Deep Reinforcement Learning from Self-Play in Imperfect-Information Games. 2016.
[31] Matthew Hausknecht and Peter Stone. Deep Recurrent Q-Learning for Partially Observable MDPs. In AAAI Fall Symposium Series, 2015.