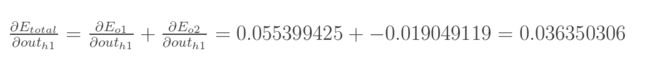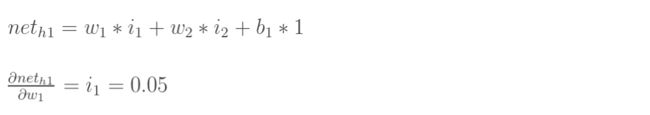机器学习笔记丨神经网络的反向传播原理及过程(图文并茂+浅显易懂)
文章目录
-
一、前言
-
二、神经网络的前向传播原理
-
1. 单个神经元的计算
-
2. 神经元在神经网络中的计算
-
-
三、反向传播算法内容(请静下心,一步一步的看)
-
Step1 计算误差
-
Step2 更新权重
-
-
四、具体例子
-
Step1 计算前向传播的误差
-
Step2 更新输出层权重
-
Step3 更新隐藏层权重
-
-
五、References
一、前言
近年来机器学习变得越来越热门,越来越多的人开始学习机器学习。在学习机器学习的时候,难免会和数学打交道。相信有一些小伙伴可能会有这样的问题,看到一些复杂的算式,哪怕是听了很多遍讲解,也感觉他说的彷佛不是人类的语言一样,比如说我。想要在深度学习岗位就业的话,有很大的可能会给你一个简单的神经网络,然后给你笔和纸,让你推导反向传播的公式。并且,在优化网络模型或是使用新的网络模型的时候,如果不知道基本原理的话,会很难操作。因此,很有必要彻底弄懂神经网络的反向传播。
本文将通过图文的方式,尽可能以最最最简单的方式来帮助大家理解神经网络的基本原理。如果是数学不是很牢靠的小伙伴想要入门深度学习的话,相信这篇文章会对你大有帮助
希望读者的大家看完文章后会有一种“啊!原来这么简单啊!”的想法。如果有不懂的地方或是文章搞错的地方,请在评论区留言,我们一起讨论精进!
接下来我会读这篇文章的内容以及必备知识进行一个说明。
必备知识
在理解神经网络的方向传播原理之前,需要掌握以下的知识:
- 偏微分的基础知识(知道什么是偏微分就行)
- 神经网络的前向传播法则
- 链式法则是什么(知道是什么就行,最重要的部分 !!!)
在本篇文章中,首先会通过一组图来让大家对神经网络的传播有个大致的印象,然后通过具体的例子来实际体验一下在反向传播时,权重是如何更新的。推荐先快速浏览一下前面的原理图,看不懂里面的式子也没关系,可以结合后面的例子理解。
二、神经网络的前向传播原理
在解释神经网络的前向传播时,将使用一个简单的全连接三层的神经网络进行说明,如下图所示。
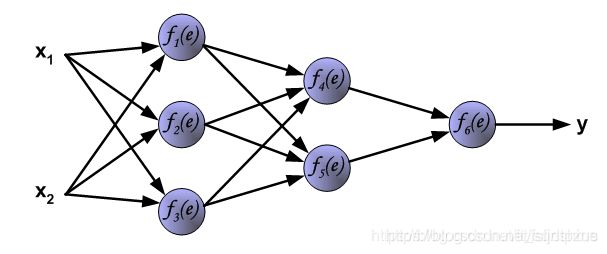
神经网络由一层一层的神经元构成(1纵列称为这个神经网络的一层),因此在学习神经网络的前向传播时,应该先知道每个神经元是如何计算的。
1. 单个神经元的计算

图中符号意义如下所示:
◆ 输入数据:x1,x2
◆ 权重参数:w1,w2
◆ 激活函数:f(e)
◆ 输出:y
神经元输出y的计算方法分为以下两步:
Step1 累加求和
输入数据和其对应的权重相乘并求和
图中的 e = x 1 w 1 + x 2 w 2 e=x_1w_1+x_2w_2 e=x1w1+x2w2
Step2 激活
将第一步的输出通过一个非线性的激活函数激活(图中f(e)),得到输出y: y = f ( e ) y=f(e) y=f(e)
2. 神经元在神经网络中的计算
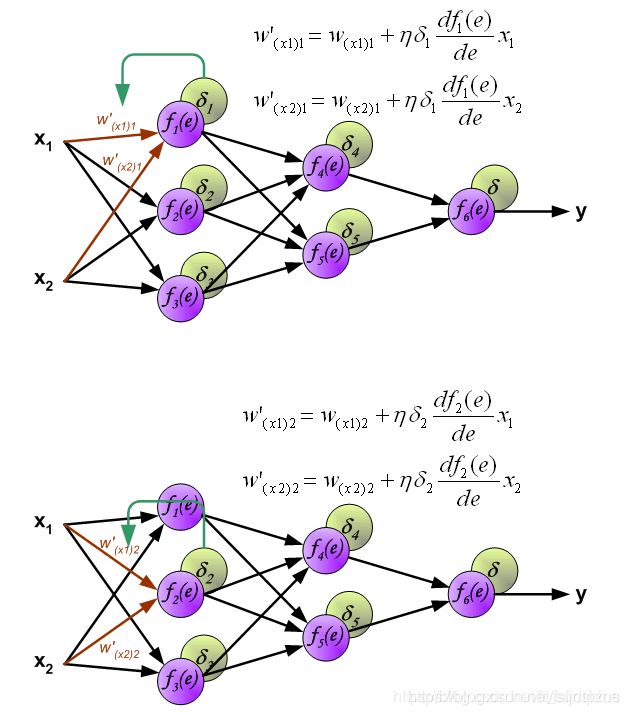
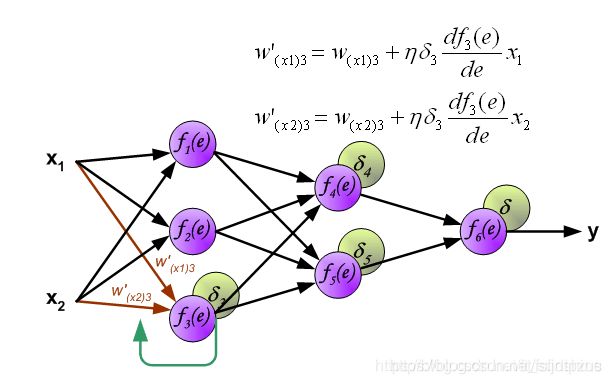
在全连接神经网络中,每一层的每个神经元都会与前一层的所有神经元或者输入数据相连,例如图中的 f 1 ( e ) f_1(e) f1(e)就与 x 1 x_1 x1和 x 2 x_2 x2分别相连。因此,在计算的时候,每一个神经元的输出=使用激活函数激活前一层函数的累加和,例如第一幅图中的 f 1 ( e ) f_1(e) f1(e)的输出 y 1 y1 y1, y 1 = f 1 ( w ( x 1 ) x 1 + w ( x 2 ) x 2 ) y1=f_1(w_(x1)x_1+w_(x2)x_2) y1=f1(w(x1)x1+w(x2)x2),下面的两个神经元的计算同理。
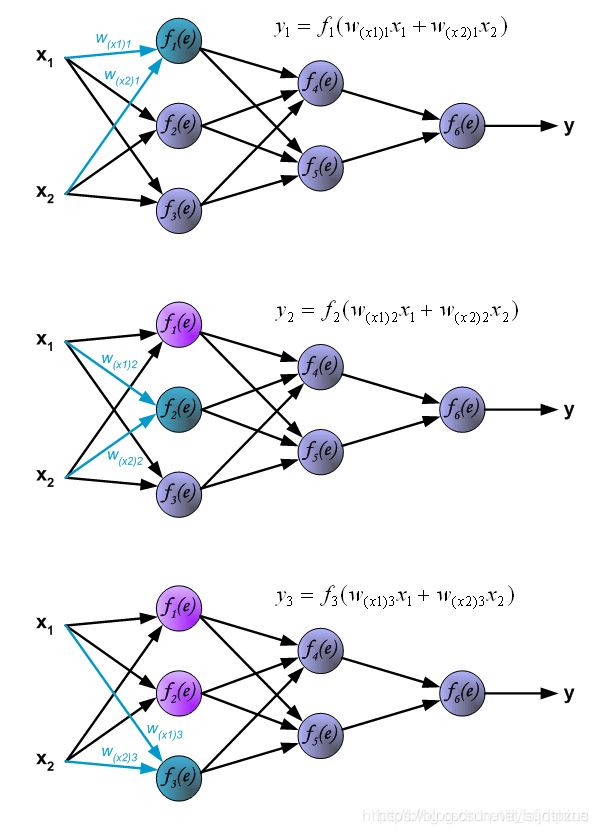
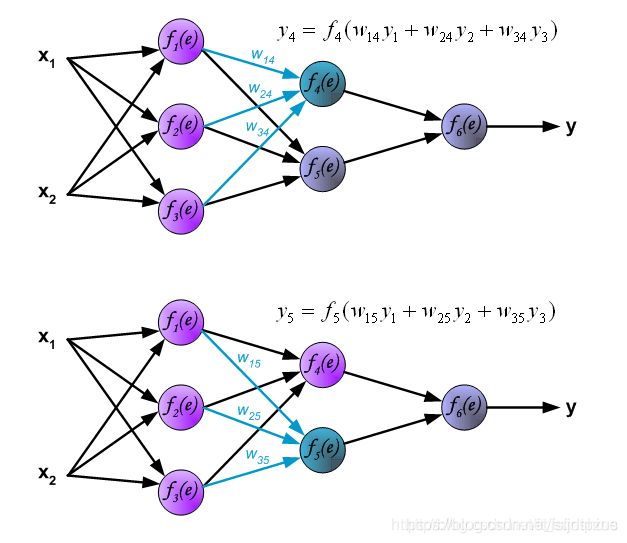
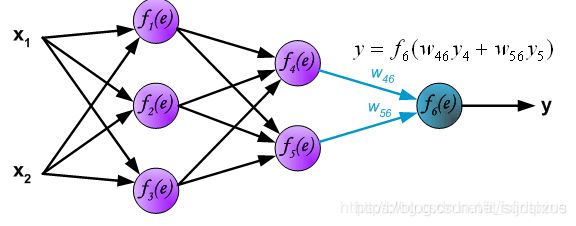
下图展示了第二层隐藏层的中神经元输出的计算方式。每一个神经元与上一层的神经元分别相连,例如 f 4 ( e ) f_4(e) f4(e)与 f 1 ( e ) f_1(e) f1(e)、 f 2 ( e ) f_2(e) f2(e)、 f 3 ( e ) f_3(e) f3(e)分别相连。计算方法与上述所述相同,例: f 4 f_4 f4的输出 y 4 y_4 y4=使用激活函数对上一层神经元的出的累加和进行激活。所有层的计算完毕后,最终输出y。
三、反向传播算法内容(请静下心,一步一步的看)
首先说一下什么是反向传播算法。
反向传播算法(Backpropagation,简称BP算法)是“误差反向传播”的简称,是适合于多层神经元网络的一种学习算法,它建立在梯度下降法的基础上。梯度下降法是训练神经网络的常用方法,许多的训练方法都是基于梯度下降法改良出来的,因此了解梯度下降法很重要。梯度下降法通过计算损失函数的梯度,并将这个梯度反馈给最优化函数来更新权重以最小化损失函数。
BP算法的学习过程由正向传播过程和反向传播过程组成。
在正向传播过程中,输入信息通过输入层经隐含层,逐层处理并传向输出层。如果预测值和教师值不一样,则取输出与期望的误差的平方和作为损失函数(损失函数有很多,这是其中一种)。
将正向传播中的损失函数传入反向传播过程,逐层求出损失函数对各神经元权重的偏导数,作为目标函数对权重的梯度。根据这个计算出来的梯度来修改权重,网络的学习在权重修改过程中完成。误差达到期望值时,网络学习结束。
神经网络的反向传播可以分为2个步骤,下面将对这2个步骤分别进行说明。
Step1 计算误差
第一步是计算神经网络的输出(预测值)和真值的误差。
图中y为我们神经网络的预测值,由于这个预测值不一定正确,所以我们需要将神经网络的预测值和对应数据的标签来比较,计算出误差。误差的计算有很多方法,比如上面提到的输出与期望的误差的平方和,熵(Entropy)以及交叉熵等。计算出的误差记为 δ δ δ.
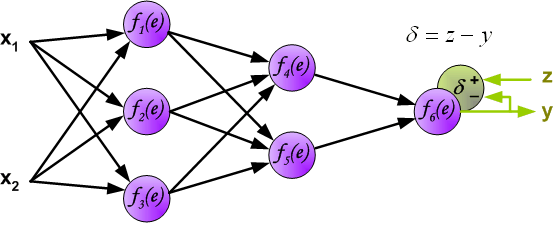
反向传播,顾名思义,是从后向前传播的一种方法。因此计算完误差后,需要将这个误差向不断的向前一层传播。向前一层传播时,需要考虑到前一个神经元的权重系数(因为不同神经元的重要性不同,因此回传时需要考虑权重系数)。
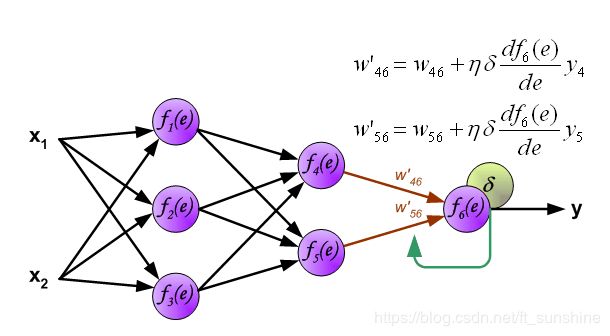
例:将误差 δ δ δ向 f 4 ( e ) f_4(e) f4(e)传播时, w 46 w_{46} w46为 f 4 ( e ) f_4(e) f4(e)的权重系数, f 4 ( e ) f_4(e) f4(e)的误差 δ 4 = w 46 δ δ_4=w_{46}δ δ4=w46δ
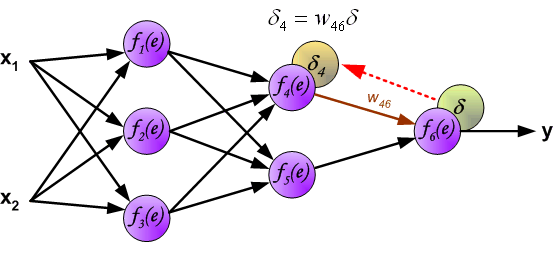
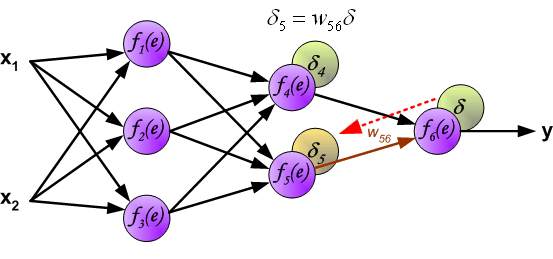
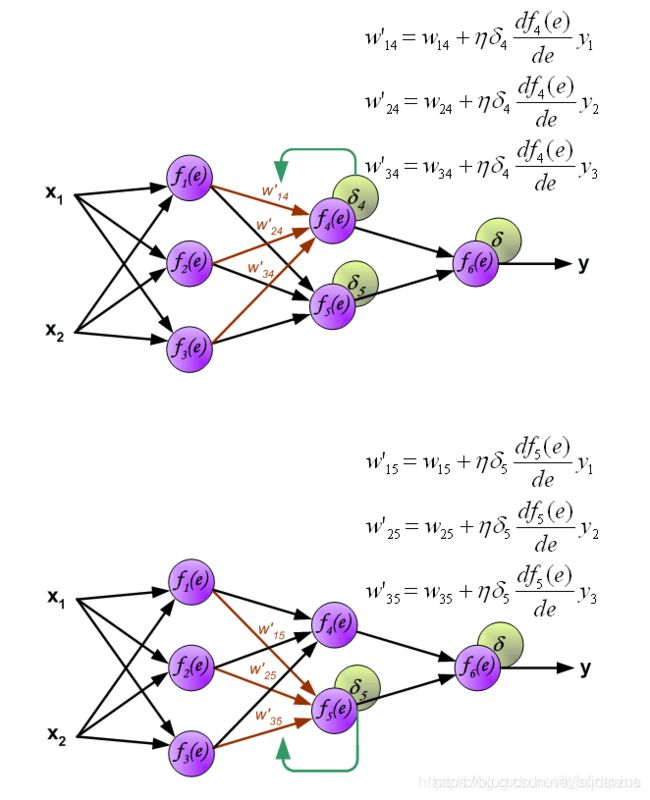
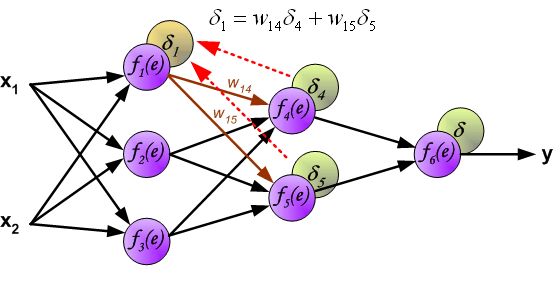
与前向传播时相同,反向传播时后一层的节点会与前一层的多个节点相连,因此需要对所有节点的误差求和。例如图中的神经元 f 1 ( e ) f_1(e) f1(e)同时与 f 4 ( e ) f_4(e) f4(e)和 f 5 ( e ) f_5(e) f5(e)相连,因此计算 f 1 ( e ) f_1(e) f1(e)的误差时需要考虑后一层 f 4 ( e ) f_4(e) f4(e)和 f 5 ( e ) f_5(e) f5(e)的权重系数,因此 δ 1 = w 14 δ 4 + w 15 δ 5 δ_1=w_{14}δ_4+w_{15}δ_5 δ1=w14δ4+w15δ5
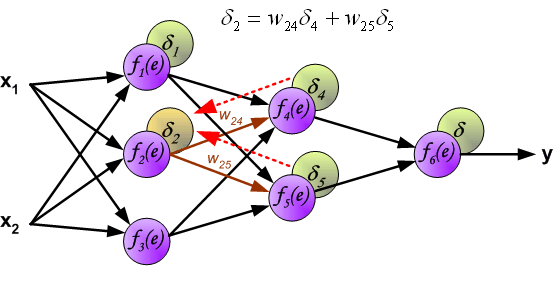
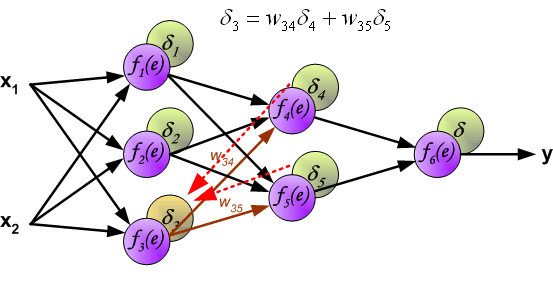
到此为止已经计算出了每个神经元的误差,接下来将更新权重。
Step2 更新权重
图中的 η η η代表学习率, w ′ w' w′是更新后的权重,通过这个式子来更新权重。这个式子具体是怎么来的,请看下面的具体事例,现在只要先保留大概的印象就行了。
四、具体例子
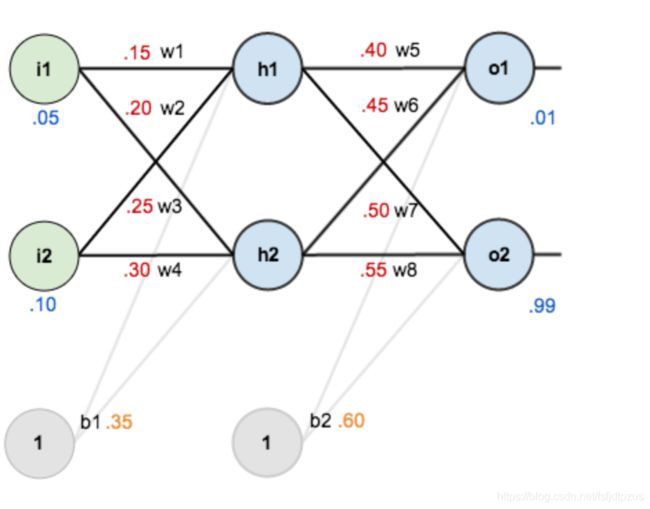
下面将通过一个具体例子来理解反向传播的具体流程。通过这个例子,来实际体会一下反向传播中的梯度以及权重是如何计算以及更新的吧。 下图是一个神经网络的结构图,其中: - 输入数据:i1=0.05,i2=0.10 - 权重系数:w1=0.15,w2=0.20,w3=0.25,w4=0.30,w5=0.40,w6=0.45,- w7=0.50,w8=0.55 - 隐藏层神经元:h1,h2 - 输出层神经元:o1,o2 - 偏置项(bias):b1=0.35,b2=0.60 - 激活函数:sigmoid
目标:给出输入数据i1, i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
Step1 计算前向传播的误差
1.输入层——>隐藏层
计算神经元h1的加权和 n e t h 1 net_{h1} neth1(未经激活函数激活):
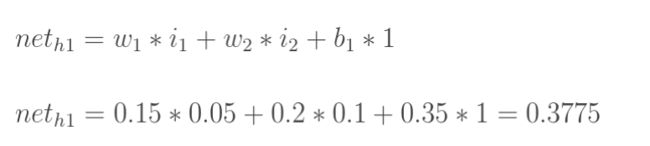
计算h1的输出 o u t h 1 out_{h1} outh1(激活后):
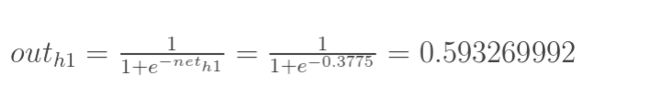
同理可以计算出h2的输出 o u t h 2 out_{h2} outh2:
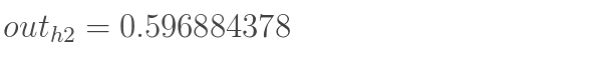
2.隐藏层——>输出层
同理可以计算出输出层的输出 o u t o 1 out_{o1} outo1和 o u t o 2 out_{o2} outo2:

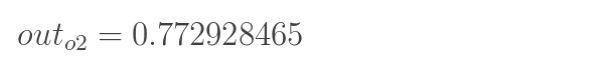
至此前向传播就结束了,我们得到的输出结果是[ o u t o 1 out_{o1} outo1=0.75136079 , o u t o 2 = 0.772928465 out_{o2}=0.772928465 outo2=0.772928465], 与目标的[0.01, 0.99]还差的很远。因此,有必要计算误差,更新权重,使预测值接近教师值。
Step2 更新输出层权重
由于隐藏层需要将相连接的多个神经元的权重求和,因此为了方便理解,这里先从一个神经元的输出层开始讲解。
1.计算误差
在我们的神经网络中,有两个输出,因此计算误差的时候需要把这两个输出的误差求和。这里计算总误差时,我们采用输出与期望的误差的平方和,即mse的计算方法来计算。
计算误差公式:
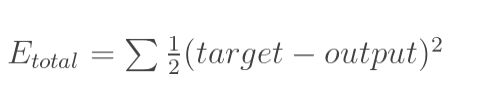
根据此公式,输出1、输出2、总误差的计算如下所示:
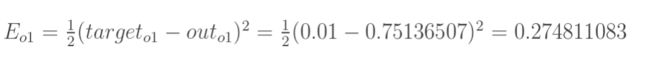

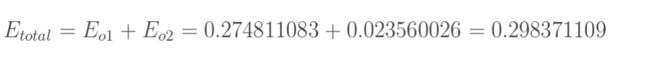
2.更新权重
更新权重时,我们需要知道这个权重对全体产生了多少影响,这个影响的大小可以用偏导数求出来。
例:对于输出层权重w5,我们可以用整体的误差对w5求偏导
下图展示了如何使用链式法则来进行反向传播的:
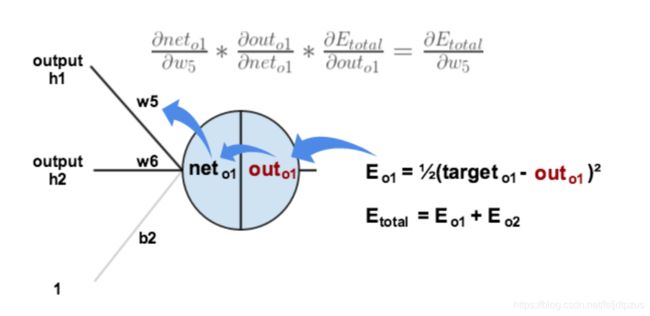
不清楚链式法则的同学,可以先想象以下有这样的一个函数。 y = f a ( f b ( w 0 , w 1 ) ) y=f_a(f_b(w_0,w_1)) y=fa(fb(w0,w1)),在这个函数中,由于是函数的嵌套,没法直接对 w 0 w_0 w0求偏导。想要对 w 0 w_0 w0求偏导的话,需要先用整个函数对外层的 f a f_a fa求偏导,然后在使用 f a f_a fa对 f b ( w 0 , w 1 ) f_b(w_0, w_1) fb(w0,w1)求偏导。链式法则就是针对这种函数嵌套问题的一种解决方法。(可以理解为套娃,想要求得最里面的偏导数就要一层一层拆开这种感觉)
针对图中的神经元,可以将其想象为以下的嵌套方式 o u t o 1 ( n e t o 1 ( w 5 , w 6 , w 7 ) ) out_{o1}(net_{o1}(w5,w6,w7)) outo1(neto1(w5,w6,w7)),因此为了求得w5对整体误差的影响,需要先用整体误差对 o u t o 1 out_{o1} outo1求偏导,再用 o u t o 1 out_{o1} outo1对 n e t o 1 net_{o1} neto1求偏导,最后使用 o u t o 1 out_{o1} outo1对 w 5 w5 w5求偏导。
了解了链式法则后,来实际看看使用链式法则对w5来进行求偏导的过程叭。
具体求解如下:
计算误差公式 ∂ E t o t a l ∂ o u t o 1 \frac{\partial E_{total}}{\partial out_{o1}} ∂outo1∂Etotal:
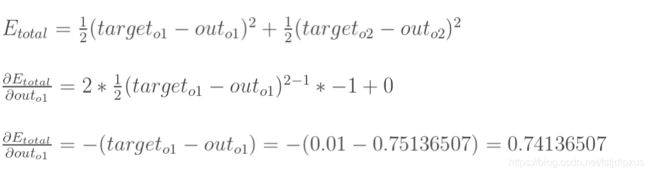
计算 ∂ o u t o 1 ∂ n e t o 1 \frac{\partial out_{o1}}{\partial net_{o1}} ∂neto1∂outo1:

这一步相当于是对激活函数sigmoid求导
计算 ∂ n e t o 1 ∂ w 5 \frac{\partial net_{o1}}{\partial w_{5}} ∂w5∂neto1:
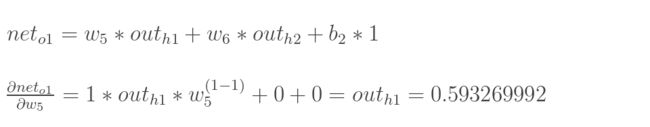
最后三项相乘得到最终的w5的偏导:

在反向传播中,我们通常使用 δ δ δ来表示误差,因此输出层o1的误差可以表现为 δ o 1 δ_{o1} δo1。
δ o 1 δ_{o1} δo1可以表示为如下形式:

因此对于计算w5对整体误差的影响的公式:
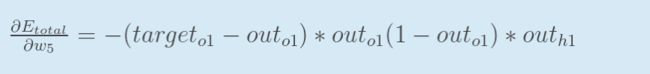
可以表示为:

如果误差为负数,也可以表示成:

根据上面的计算式,来更新w5的权重:

其中η是学习率,这里取0.5
同理更新w6,w7,w8:

Step3 更新隐藏层权重
更新隐藏层的方法,与更新输出层的权重系数的方法类似,但是有一点需要注意。
在更新输出层权重系数w5的时候,我们使用链式法则,通过out(o1)→net(o1)→w5求出。
| 注意!此时神经元o1的求导路径只有一条! |
在更新隐藏层权重系数w1,使用链式法则时,通过out(h1)→net(h1)→w1求出,如下:
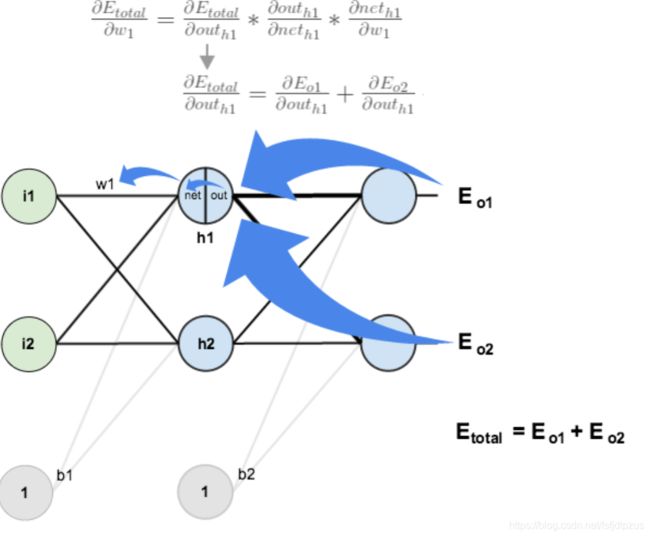
| 注意!这个时候神经元o1的求导路径有2条(如蓝色箭头所示)! |
----------------下面将根据图中的等式,实际计算并更新w1的权值----------------
I: 计算第1部分的偏导数 ∂ E t o t a l ∂ o u t h 1 \frac{\partial E_{total}}{\partial out_{h1}} ∂outh1∂Etotal:

先计算 ∂ E o 1 ∂ o u t h 1 \frac{\partial E_{o_1}}{\partial out_{h1}} ∂outh1∂Eo1:

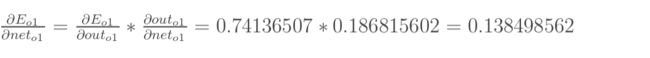
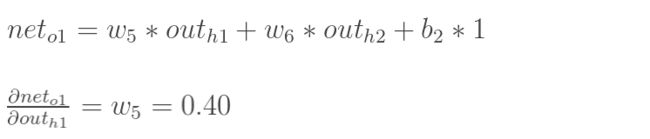
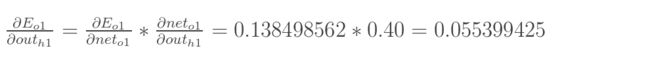
同理可以计算出 E o 2 o u t h 1 \frac {E_{o2}}{out_{h1}} outh1Eo2

II: 计算第2部分的偏导数 ∂ o u t h 1 ∂ n e t h 1 \frac{\partial out_{h1}}{\partial net_{h1}} ∂neth1∂outh1:
III: 计算第3部分的偏导数 ∂ n e t h 1 ∂ w 1 \frac{\partial net_{h1}}{\partial w_{1}} ∂w1∂neth1:
IV: 三者相乘,计算h1节点对w1的偏导数 ∂ E t o t a l ∂ w 1 \frac{\partial E_{total}}{\partial w_{1}} ∂w1∂Etotal:
至此,就计算出了神经元h1的误差。
将上面的计算步骤整理,可得如下公式:

其中,累加符号表示将不同路径的误差相加,此时的路径有两条(图中的两个蓝色箭头)。同时,将计算输出层的误差时说到,计算时使用 δ δ δ来表示误差,这里的 δ h 1 δ_{h1} δh1代表神经元h1的误差。
得到了神经元h1的误差,就可以根据之前的权重系数以及误差来更新权重系数了。
更新h1的权重系数:

至此,1个神经元的权重系数的更新就完成了。其中的 η \eta η代表学习率,通常在程序中指定,可以理解为梯度下降法中的步长。
同理,更新w2,w3,w4的权重系数:

至此,反向传播就结束了。将这个过程不断重复,就可以不断减小误差,提高正确率,获得比较好的模型了。
在学习反向传播的时候,面对这些种种的公式,当时又是犹豫又是搞不懂。希望和我有一样困扰的人,可以借助这些图来理解,不要绕远路。
如果觉得本文比较好理解的话,可以【点赞 + 关注】,以后我会不断更新图文并茂的文章的。
同时,如果有不懂的地方可以在评论区留言,只要我看到就会立刻回复。
五、References
[1]. 图片来源
[2]. “反向传播算法”过程及公式推导(超直观好懂的Backpropagation)
[3]. 一文弄懂神经网络中的反向传播法——BackPropagation