python-opencv:图像直方图，及其应用总结

本篇文章把直方图到对于图像的直方图基本应用和比较全部讲完了。很长，对于小白来说需要理解的地方较多，请细读。

---

---

一. 直方图是什么

1. 直方图

直方图是一种统计报告图，它一般表示不同类型数据的分布情况。如下就是一种简单的直方图。

直方图在统计中很常用，而在学习python及图像处理模块，统计也是必不可少的操作。因此很多开源库都会自带绘制直方图的方法。下文介绍一种常用的库，它带有很多统计绘图操作，在python学习中无比重要。

2. 利用matplotlib绘制简单直方图

①. matplotlib

Matplotlib 是一个 Python 的 2D绘图库，它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形，值得注意的是，matplotlib在很多方面与matlib十分相似，甚至渐渐的在某种程度上替代matlib的，随着python的发展，可能这个现象应该会越来越明显。

②. matplotlib安装

利用pip命令安装。

pip install matplotlib -i http://pypi.douban.com/simple/

注意命令后是换源。

②. 绘图代码

如下是利用matplotlib绘制一个简单的直方图代码：

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False

array=np.array([1,1,1,5,5,3,1,5,23,1,5,32,1,1,23,4,1,2,5,4,13,13])
plt.hist(array,40,[0,40])
plt.show()

结果如下：

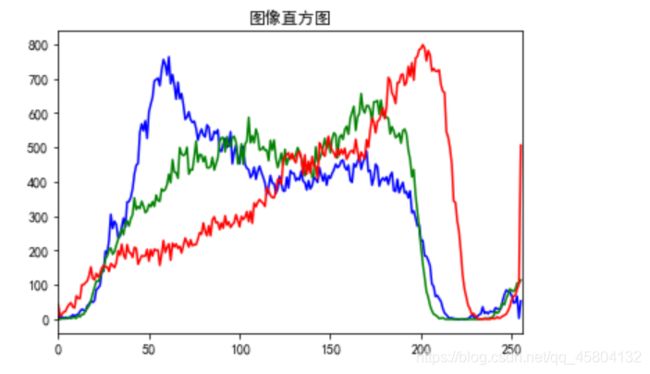
前文主要说了直方图这个东西，为什么要说它。。是因为图像直方图，与我们常规理解的直方图似乎有些不太一样。。如下是一个简单的图像直方图，其实它本质也是直方图，只是由于刻度条变得很密，所有就没有那么“直方”了。

二. 图像直方图

1. 图像直方图

图像直方图由于其计算代价小等特点，在图像分割，图像检索，等多领域都有很大的用处，上图就是一个很完整的图像直方图。我们在有一个图像信息后，对其像素点，或者其他信息进行收集可以绘制不同的图像直方图，这里仅从像素点入手。

2. 以一张图像绘制直方图

**import cv2 as cv 
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False

#加载图像
def load_image():
    src=cv.imread('bi.jpg')
    #cv.imshow('input',src)
    return src
def show_and_plot():
    src=load_image()
    #plt.hist(src.ravel(),256,[0,256])
    #plt.show('直方图')
    color=['blue','green','red']
    for i,c in enumerate(color):
        hist=cv.calcHist([src],[i],None,[256],[0,256])
        plt.plot(hist,color=c)
        plt.xlim([0,256])
    plt.title('图像直方图')    
    plt.show()
    
show_and_plot()

结果如下：

3. 代码解析

plt.rcParams[‘font.sans-serif’] = [u’SimHei’]
plt.rcParams[‘axes.unicode_minus’] = False

这两行代码是在jupyter notebook绘图中显示中文的必备代码，否则会乱码。

enumerate()

是python中的基本方法，返回一个enumerate迭代序列。该迭代序列一般由多个元组组成，每个元组含有两个元素，第一个元素是索引，第二个元素是序列中对应的元素。如下：

hist=cv.calcHist([src],[i],None,[256],0,256)

是OpenCV中自带的绘制直方图的API，其需要与matplotlib配合绘图，它可以构建整个直方图的结构，在plot之中只需要添加颜色就可以将整个直方图绘制出来。

• src:原图，需要用[]括起来。
• i:通道，需要用[]括起来。
• None:这里是掩膜，掩膜是什么之前已经讲过了。可翻之前的博客。
• 256是柱子数要用[]括起来，我感觉这设定很奇怪但是。。就是这样。。

np.array.ravel()

该方法是返回了一个视图，emm说白了就是对数组进行了多维降为一维，并且对该一维数组的操作也会直接影响到原先的数组。可以实现对数组降维的还有另一种方法，但是两种方法稍有不同。

np.array.flatten()

该方法实现了对矩阵的降维同时copy，对获取后的矩阵操作并不会影响原矩阵。如下是一个明显的比较。

#flatten返回矩阵的拷贝，且对其操作不影响原矩阵，而ravel返回矩阵的视图，对其操作影响矩阵，从本质来说，都属于将多维降为1维
import numpy as np

#获取一个随机的矩阵
s=np.random.normal(0,20,(3,3))
print('矩阵为:',s)
print('ravel降维后',s.ravel())
s.ravel()[0]=100
print('ravel改变后，原矩阵:',s)

s=np.random.normal(0,20,(3,3))
print('矩阵为:',s)
print('flatten降维后',s.flatten())
s.flatten()[0]=100
print('flatten改变后，原矩阵:',s)

结果为：

三. 图像直方图的应用

1. 全局直方图均衡化

①. 直方图均衡化

官方阐述：直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。通过这种方法，亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能

其实可以用图片以及很浅显的语言来解释这段话。

我们来看右边的两张图，上图表明，像素点大多分布在亮度低的范围内，而亮度高的范围几乎没有像素点，这样整张图片就显得很暗。。没有对比度，而均衡化就将上图那种不均衡的分布变得很均衡，在亮度高和亮度中等的为止明显多了分布，因此，图像的表现性就会很强，而整体的效果就是实现了对比度的增强。直方图均衡化的方法包含全局的直方图均衡和部分的直方图均衡，虽然说我们知晓原理之后在python基础足够的情况下已经可以实现简单的直方图均衡化，但是还是建议直接调用API，他们的算法效率往往比我们这些“涉世未深”的程序员要高的多。其实直方图均衡化从数学角度分析也有很多的原理，但是这里就不阐述了，又是一大把东西，大家把基本的原理看懂就ok了，之后有机会在从数学角度说吧。

②. 直方图均衡化代码实现

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt


def load_image():
    image=cv.imread('test.jpg')
    return image
def equal_all_hist(image):
    image=cv.cvtColor(image,cv.COLOR_BGR2GRAY)
    #需要单通道图
    return cv.equalizeHist(image)

def show_and_compare():
    image=load_image()
    cv.imshow('image',image)
    image_1=equal_all_hist(image)
    cv.imshow('image_1',image_1)
    cv.waitKey(0)
    cv.destroyAllWindows()
show_and_compare()

效果如下：

③. 代码解析

cv.equalizeHist(image)

该方法仅有一个参数，就是原图，其他方面算法都已经包装好，因此不必担心。
我们在调用全局的直方图均衡化时特别要注意的一个问题就是该API单方面对单通道图起作用，可以用[:,:,1],也可以用[:,:,0]，或者转化为灰度图都可以，但是不可以用多通道图。

我们可以看到该API对这张图表现很好，但是事实上，全局的直方图均衡并没有想象中效果那么好，因为它是对全局操作的，因此，我们需要特别表现的部分并没有表现出来，由下图可以看出，它的表现性并不好。因此我们常用的应该是局部的直方图均衡化。

2. 局部直方图均衡化

①. 局部直方图均衡化

局部直方图均衡化与以上方法的区别也很明显，它并非直接对整体的图像进行操作的，而是将图像分为一个个块进行操作的，这样的话从局部角度来考虑就可以使每一部分需要表现的部分变的更强，整体下来，我们特别需要表现的部分就会变得很强。

②. 代码实现

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt


def equal_part_hist(image):
    image=cv.cvtColor(image,cv.COLOR_BGR2GRAY)
    clahe=cv.createCLAHE(clipLimit=5.0,tileGridSize=(8,8))
    image=clahe.apply(image)
    return image

def show_and_compare():
    image=load_image()
    cv.imshow('image',image)
    #image_1=equal_all_hist(image)
    image_2=equal_part_hist(image)
    #cv.imshow('image_1',image_1)
    cv.imshow('image_2',image_2)
    cv.waitKey(0)
    cv.destroyAllWindows()
show_and_compare()

效果如下：

该方法在细节方面是明显要强于全局的直方图均衡化的，可以做比对：

因此，一般情况下是更推荐使用局部直方图均衡化的，当然也有其他特殊情况，就看个人自己考虑了。

③. 代码解析

核心

clahe=cv.createCLAHE(clipLimit=5.0,tileGridSize=(8,8))
image=clahe.apply(image)

• 构建一个clahe对象，利用该对象对图像进行操作。
• 参数1：clipLimit表示的对比度的限制。tileGridSize：表示选取的像素区域大小。

运算原理:我们在设定了对比度的限制之后，该方法会从坐标开始选取设定好大小的区域开始计算，如果该区域的对比度超过了限制，那么首先会考虑超限的问题，将高点或者低点进行一个磨匀的操作，这样就防止了噪声被放大。之后才会继续做均衡化。

四. 图像直方图的比较

1. 直方图的比较

直方图比较一般用来做对图像的信息比对。一般来说，如果直方图的比对结果符合某种结果我们就认为两张图像是相同的。（拼图除外）对于计算机来说，它目前不可能像是我们人类一样，用视觉去观测图片，看他们是否相同，因此计算机常用几种参数去判断图像的相似度，这里的应用就会比较广了，车牌识别啊，人脸识别等等。。。

2. 几种比较

①. 巴氏距离

在统计中，巴氏距离用于度量两个概率分布的相似性，其实在图像识别中，就是判断两者的不同像素点的分布情况，如果完全匹配，则为1，完全不匹配则为0，当然，一般不太可能出现完全不匹配的两张图

②. 相关性

相关性，学习过高数，就差不多明白了，我们会接触一个线性相关，学习机器学习基础后，也必须要掌握相关性的概念，它的取值范围为[0,1]若为1则完全相关，从线性角度来说，若是完全相关，意味着x和y符合某种必然的线性关系。从图像的角度来说。。相关性越高则意味着图像越像。

③. 卡方

说到卡方这里需要说到一种检验方法：卡方检验。
卡方检验是一种是针对与分类变量的假设检验方法。它一般做分类资料的相关分析。是一种非参数检验，有兴趣学习的话可以去该博客稍作学习。我们只需要理解一句话
卡方检验一般是看观测值和实际值的差异，对于图像来说，我们只需要知道越相似，则卡方值越小，否则越大。

* 3. 代码实现（重点）

这里要注意该代码可以在没人讲解的情况下需要一段时间去理解，不过这里我尽量讲清楚。

import cv2 as cv
import numpy as np

#创建三通道直方图
def creat_rgb_hist(image):
    h,w,ch=image.shape
    #初始化
    rgb_hist=np.zeros([16*16*16, 1], np.float32)
    #定义binsize 这里直接定义16为一个bin
    bin_size=16
    for i in range(h):
        for j in range(w):
            b,g,r=image[i,j]
            #获取索引
            index=np.int((b/bin_size)*16*16 +(g/bin_size)*16+(r/bin_size))
            #对应像素点数量自加
            rgb_hist[index,0]+=1
    return rgb_hist
def hist_compare(image1, image2):
    hist1=create_rgb_hist(image1)
    hist2=create_rgb_hist(image2)
    match1=cv.compareHist(hist1, hist2, cv.HISTCMP_BHATTACHARYYA)
    match2=cv.compareHist(hist1, hist2, cv.HISTCMP_CORREL)
    match3=cv.compareHist(hist1, hist2, cv.HISTCMP_CHISQR)
    print("巴氏距离: %s, 相关性: %s, 卡方: %s"%(match1, match2, match3))
    cv.imshow("image1",image1)
    cv.imshow("image2",image2)
    
image1 = cv.imread("test_1.png")
image2 = cv.imread("test_2.png")

hist_compare(image1, image2)
cv.waitKey(0)
cv.destroyAllWindows()

结果如下：

* 4. 代码解析（重点）

首先我们来看创建三通道直方图

• 这里首先是用shape获取图片的高，宽与通道数，接着我们创建了一个[161616]的矩阵，并且命名了一个16的binsize，这里主要这个16与矩阵中的16是相辅相成的，很明显16*16=256，我们后面直接需要用到这个binsize统计频数，这样会比每个像素点要快很多，自己理解。这里我们也可以将矩阵改为32-32-32，当然对应的binsize，要改为8。

cv.compareHist(src_1,src_2,cv.XXXXX)

该方法是OpenCV提供的比对方法，其参数并不难，总共三个，图像一，图像二，比对参数，其中最重要的是比对参数。

• 巴氏距离：cv.HISTCMP_BHATTACHARYYA
• 相关性：cv.HISTCMP_CORREL
• 卡方：cv.HISTCMP_CHISQR

这几种数值的范围及大小代表的情况前文已经说过了。可能就仅上图的数值而言，我们
会觉得这个卡方好大。两万多，其实并不是，卡方在图像比对中值会非常跳跃，我们可以用两张完全不同的图片来比对。

看到没两千多万，而且这两张图并非是完全不相似的，他们都是油画风格的。如下：

所以一般情况下卡方几万的话就已经很小了，如果几千，甚至几百，那基本可以视为一模一样的图片，我们要对卡方的数值有概念。

五. 总结和建议

• 以上几乎每一种理论都有其计算公式，这些公式有时候很复杂，但是并不妨碍我们将其分解开来理解，举个简单的例子。
  
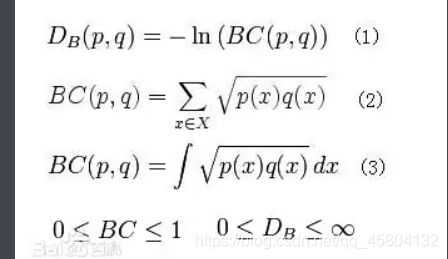
  如上就是巴氏距离在百度百科上的分解公式，它无非就是一个函数，一个积分，我们将其一个个展开来很容易推导和理解。

• 纵观全篇文章，主要围绕应用为主，因此原理方面没有阐述太多的数学理论，但是数学理论依然是必不可少的，只是对于初接触该方面或者我们这些低年级的同学来说，接触应用和白话理论可能更容易一些。

• 以上的代码还是建议小伙伴们在脱离了文章的情况下去自己能敲出来，代码能力是程序员的核心之一。

• 文章所标注的两个重点部分请务必反复阅读通透为止，因为我之前在b站看某老师讲课时，我发现有很多同学在这部分没有看明白，或者说也有可能是老师没有讲明白，鄙人虽然没有很聪慧，但是悟性也不能说差，这里的内容看了两遍才彻底看明白，但是言语表达又稍微有些无力，虽然我已经把核心的部分说出来了，还是需要去注意理解。

• 文章内部掺杂了一些其他的内容，可能会有小伙伴觉得是没用的东西，没必要去看，去了解，但是我解释一下吧，我们在学习一个大方向时，会遇到各种各样的问题，我们去搜一个问题，它又会重复一个递归的过程到一个更基本的问题，而沿途的这些知识点也是需要积累的，它的过程或许很慢，但一定不是坏事，这也是我一直逼自己的学习方式。只是也要量力而为，有些东西确实理解不了就先放着，慢慢去嚼，随着知识的积累，总有一天会通透的。