【笔记】数据方法论-2.1.推断统计分析-参数估计

写在前面

• 重点知识
  • 点估计与区间估计的概念和区别
  • 中心极限定理的含义
  • 正态分布及其特性

1.推断统计分析概述

1.1 总体、个体与样本

• 总体：包含我们要研究的所有数据
• 个体：总体中的某个数据，就是个体
• 样本：从总体中抽取部分个体，就构成了样本
• 样本是总体的一个子集；样本中包含的个体数量，称之为样本容量

1.2 推断统计概念

• 推断统计研究如何根据样本数据去推断总体数量特征的方法。是在对样本数据进行描述性统计的基础上，对总体的未知数量特征做出以概率形式表述的推断。
• 进行推断统计的原因：在实际研究中，获取总体数据通常比较困难，甚至不可能完成。因此就需要对总体进行抽样，通过样本的统计量去估计总体参数。
• 总结：总体的参数通常是未知的，为了获取总体的参数，就需要通过样本的统计量来估计总体参数。

2.点估计与区间估计

2.1 点估计

• 点估计：使用样本的统计量代替总体。例如，求鸢尾花的平均花瓣长度，就可以使用样本的均值估计总体的均值

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris

sns.set(style='darkgrid')
plt.rcParams['font.family']='SimHei'
plt.rcParams['axes.unicode_minus']=False

iris = load_iris()
data = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
data = pd.DataFrame(data,
                   columns=['sepal_length','sepal_widht','petal_length','petal_width','type'])
print(data['petal_length'].mean())

• 点估计实现简单，但是容易受到随机抽样的影响，无法保证结论的准确性。
• 但是点估计因为样本来自于总体，样本还是能够体现出一些总体的特征。

2.2 区间估计

• 区间估计：根据样本的统计量，计算出一个可能的区间与概率(信心指数)，表示总体的参数会有多少概率位于该区间中。
• 区间估计指定的区间，称之为置信区间
• 区间估计指定的概率，称之为置信度
• 举例
  • 鸢尾花花瓣的长度有70%的可能性在3.4~3.8cm之间，3.4~3.8cm就是置信区间，70%就是置信度

2.3 点估计与区间估计：

• 点估计：
  • 优点：能够给出具体的估计值
  • 缺点：缺乏准确性
• 区间估计：
  • 优点：能够给出合理的范围及信心指数
  • 缺点：不能给出具体的估计值

3.中心极限定理

3.1 定理概念

如果要确定置信区间与置信度，我们首先要知道：总体与样本之间存在着怎样的联系。
在数学上，中心极限定理给出了解释说明：

如果总体（总体的分布不重要）均值为μ，方差为${\sigma }^2$，当n增大时，则样本均值逐渐趋近服从正态分布：
$\overline{X}$~N(μ,${\sigma }^2$/2)

由此可以得到如下结论：

• 1.进行多次抽样，则每次抽样会得到一个均值，这些均值会围绕在总体均值左右，呈正态分布。
• 2.当样本容量n(一般为30以上)足够大时，样本均值服从正态分布。
  • 样本均值构成的正态分布，其均值等于总体均值μ
  • 样本均值构成的正态分布，其标准差等于总体标准差$\sigma$除以$\sqrt{n}$
• 说明：
  • 样本均值分布的标准差，称为标准误差，简称标准误
  • 要明确区分总体的标准差、样本的标准差及标准误(样本均值的标准差)
  • n是样本容量，不是抽样次数

3.2 代码演示

# 生成总体数据
# loc:均值
# scale：标准差
# size:数组中含有的元素的个数
all_ = np.random.normal(loc = 50,scale=99,size=10000)
'''
np.random.normal():
生成一个平均值为50,
标准差为99，
含有10000个元素的正态分布数组
'''
# 创建一个含有1000个元素的数组，用来存放每次抽样(每个样本)的均值
mean_arr = np.zeros(1000)
# 通过循环获取1000个原本：
for i in range(len(mean_arr)):
    # 随机抽样，计算每个样本的均值，并存入数组中
    # size：样本容量
    # replace：是否放回抽取的样本，默认True，此处为False，表示不放回，每次抽取的样本的个体互不重复
    mean_arr[i] = np.random.choice(all_,size=80,replace=False).mean()
# 样本的均值构成正态分布，该正态分布的均值等于总体均值
# 该正态分布的标准误等于总体的标准差/根号n
print('样本均值构成的正态分布的均值：{}'.format(mean_arr.mean()))
print('样本均值构成的正态分布的标准误：{}'.format(mean_arr.std()))
print('样本均值构成的正态分布的偏度：{}'.format(pd.Series(mean_arr).skew()))
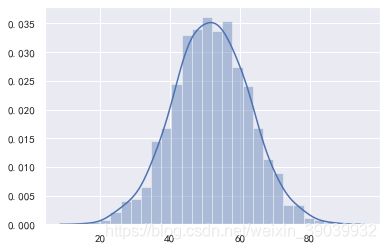
# 可视化样本均值
sns.distplot(mean_arr)

4.正态分布的特性

4.1 正态分布特性解析

在正态分布中，均值、中位数与众数是相等的。
越靠近均值的数据越多，反之越少。
如下图：

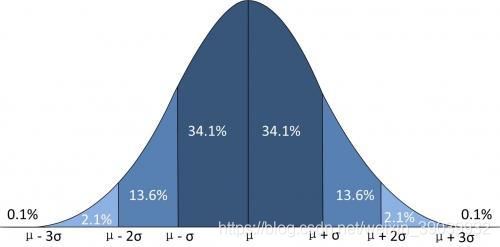
• 在正态分布中，数据分布比例如下：
  • 以均值为中心，在1倍标准差内( $\overline{x}$ - $\sigma$,$\overline{x}$ + $\sigma$)，包含约有68%的样本数据
  • 以均值为中心，在2倍标准差内($\overline{x}$ - 2$\sigma$,$\overline{x}$ + 2$\sigma$)，包含约有95%的样本数据
  • 以均值为中心，在3倍标准差内($\overline{x}$ - 3$\sigma$,$\overline{x}$ + 3$\sigma$)，包含约有99.7%的样本数据

4.2 代码演示-正态分布特性验证

# 定义总体数据的标准差
scale = 50
# 定义总体数据
data = np.random.normal(loc=0,scale=scale,size=10000)
# 定义标准差倍数：1~3
for i in range(1,4):
    result = data[(data > -i * scale) & (data < i * scale)]
    print("{} 倍标准差".format(i))
    print("包含 {:.2f}% 的数据".format(len(result) / len(data) * 100 ))

• 根据中心极限定理，如果多次抽样(总体均值为μ，方差为${\sigma }^2$)，则样本均值($\overline{X}$)构成的正态分布，满足$\overline{X}$~N(μ,${\sigma }^2$/2)。
• 如果我们只对总体进行一次抽样，则该样本的均值有95%的概率会落在($\overline{x}$ - 2$\sigma$,$\overline{x}$ + 2$\sigma$)范围内，有5%的概率会落在($\overline{x}$ - 2$\sigma$,$\overline{x}$ + 2$\sigma$)之外的地方。
  根据小概率事件定义(很小的概率在一次抽样中基本不会发生)，如果抽样的样本均值在($\overline{x}$ - 2$\sigma$,$\overline{x}$ + 2$\sigma$)之外，我们就可以认为，本次抽样的总体，该总体的均值并非是我们期望的均值
• 通常我们以2倍标准差作为依据，以样本均值为中心，正负2倍标准差构成的区间，就是置信区间。而2倍标准差包含了95%的数据，因此，此时的置信度为95%，简言之，我们有95%的信心认为总体的均值会在置信区间之内

4.3 习题解析

某事曾经统计过该市所有年龄在10~15岁儿童的平均身高，结论是标准差为13.3CM，由于某些原因，均值丢失，现对各学校中100个符合条件的学生进行测量，得出平均值为155cm，标准差为12.4cm。问：该城市在规定年龄段儿童的平均身高可能为多少？(95%置信度)

• 解析：
• 根据题目可知：
  • 总体标准差$\sigma$为13.3CM
  • 样本容量n为100
  • 样本均值$\overline{x}$为155cm
  • 置信度95%就是以样本均值为中心，正负两倍样本标准差之内
• 答案：
  • 样本的均值 ± 2 * 总体标准差/根号样本容量
  • 155 ± 2 * (13.3 / $\sqrt{100}$)

4.4 代码演示-样本推测总体均值

# 使用随机数生成总体均值，值未知
data_mean = np.random.randint(-10000,10000)
# 总体标准差
data_std = 50
# 样本容量
sam_n = 99
# 随机生成总体数据
data = np.random.normal(loc=data_mean,scale=data_std,size=10000)
# 从总体中抽取n个样本,不放回抽取
sam = np.random.choice(data,size=sam_n,replace=False)
sam_mean = sam.mean()
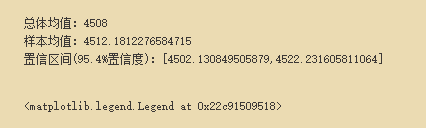
print("总体均值：{}".format(data_mean))
print("样本均值：{}".format(sam_mean))
# 计算标准误差
se = data_std / np.sqrt(sam_n)
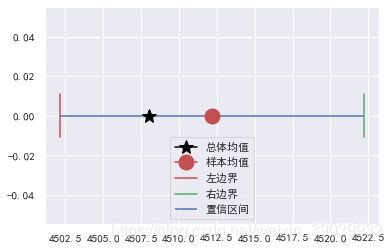
# 可视化
plt.plot(data_mean,0,marker='*',color='black',ms=15,label='总体均值')
plt.plot(sam_mean,0,marker='o',color='r',ms=15,label='样本均值')
min_ = sam_mean - 2 * se
max_ = sam_mean + 2 * se
print("置信区间(95.4%置信度)：[{},{}]".format(min_,max_))
# 绘制0轴线
plt.hlines(0,xmin=min_,xmax=max_,colors='b',label='置信区间')
# 绘制垂线，标识95.4%置信区间范围
plt.axvline(min_,ymin=0.4,ymax=0.6,color='r',label='左边界')
plt.axvline(max_,ymin=0.4,ymax=0.6,color='g',label='右边界')
plt.legend()