EM（expectation maximization）算法的理解和证明

本文记录个人对EM算法的理解

首先为什么要使用EM算法，他适用于哪些场景呢？
大家都知道EM算法是聚类算法的一种。 这个算法是在数据已知的前提下讨论参数的合理性。
换一句话说， 他是可以用似然函数建模的。等下会记录如何用数学语言描述这个算法。但是首先先使用经典的投硬币的问题将这个抽象的算法形象化。

什么情况下我们要使用 EM算法呢
假设我们现在有2枚硬币，分别记为硬币A 和硬币B，如果我拿起硬币A 投了5次得到了以下的结果：A:[+,+,-,-,+] 。这里“+”表示硬币正面朝上，“-”表示反面朝上。之后我拿起硬币B我也投5次得到了以下的结果B：[-,-,+,+,+]。 那么现在想要求到A出现正面的概率和B出现正面的概率是很简单的。

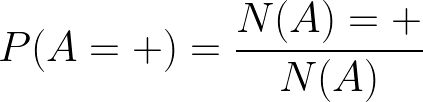
上述公式中N(A)所表示的是A抛的总次数，N(A)=+ 意思是在这些次数中出现正面的次数。
同理B出现正面的概率也可以用同样的方式表示。可以记为：

上述两个式子相对比较好理解。但是现在请设想这样一个情况。
我从AB两枚硬币中随机取一枚来投掷，并记录下投掷结果。经过N次这样的投掷之后，我也可以得到一组记录着正反面的数据。但是如果只给你这样一组数据，告诉你这一组数据是随机投掷AB两枚硬币产生的，有没有可能求出硬币A出现正面的概率和硬币B出现正面的概率呢？？这个时候就可以考虑使用EM算法了！

EM 算法的一般思路

这个问题和最开始的那一个投硬币的问题不同在哪里？
其实我们仔细的看看，会发现这一个问题中，我们不知道每一次投掷硬币的结果到底是A产生的还是B产生的，要是知道了就和最开始的那一个投硬币问题一样了。但是问题是我们不知道，而且它潜移默化地影响着我们最后的计算结果。 这种我们无法从数据中直接观测到的，但是又影响着最后模型输出的变量，我们叫它 ‘隐变量 / 潜变量’（Latent variable）

那这个时候我们就应该想方设法的把这个隐变量给表示出来呀！
假设我们现在有一个由投掷AB两枚硬币产生的一组结果 T：[+,+,-,-+,-]. 我们可以用另一个概率分布Q 来表示每一个结果是由A或者B产生的概率，用 Z 来表示那个隐藏变量（那么我们先明确隐藏变量 Z 其实就只有两个值呀！除了A就是B，不可能有C的情况出现，对吧！）。那么现在，我们就可以假设在 T 这一组结果中由A产生的概率是 Q(Z=A) ,同理也可以假设由B产生的概率是 Q(Z=B).那么这个时候求得A和B出现正面的概率也就不是难事了呀~

假如，我初始化Q(Z=A)=0.4, Q(Z=B)=0.6，那么在T中出现的3个正面朝上的结果中，就有
3 x 0.4 = 1.2 个是由硬币A产生的，3 x 0.6 = 1.8个是硬币B产生的。那同样的，在T中所有反面结果中，由A这个硬币产生的概率就是 3 x 0.4 = 1.2, 由B产生的概率是 3 x 0.6 = 1.8
那么这样一来 这个问题是不是就变成了最开始的那个最简单的投硬币问题了呢？
所以A出现正面和B出现正面的概率就可以这样来计算了（我们在这里把这两个概率用θ来表示吧~）：


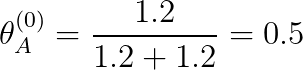
（这个概率看上去好像很符合我们得到的数据，但是这是因为为了方便计算我举了一个很简单的例子啦~。真实情况比这个要复杂哦！）
得到这个之后我们继续！现在这个问题已经和最开始的那个投硬币的问题一样的，知道数据，知道两枚硬币出现正反面的概率了！但是这个值不一定准确！！！ 因为所有的前提都是我们随机初始化的，现在我们要做的就是要来优化我们的θ，争取找到最好的那一个θ。可以想想爬山的例子来帮助理解，你想去山顶，将你随机置于山上一个地方，然后一点一点向上爬的感觉。具体怎么做其实很简单。
既然现在我们已经知道了AB出现正反面的概率了，那么我们可以用这个概率去更新我们的Q，然后再用新的Q又更新θ，一直执行这个过程直到收敛！这里画个图可能会更加的直观一点儿~。这个更新的过程就类似图中所示 （图有点佛系。。。。）
这个过程一直进行直到收敛。收敛的条件可以是我们已经找到了最好的那个θ了，自然可以退出循环了。或者是达到了最大的迭代次数，也可以作为收敛条件。

所以正如算法的名字所述，整个算法的步骤就只有两步Expectation(E-step) 和 maximization（M-step）。从上文的描述中，可以我们在更新Q的那个过程其实就是在做Expectation。更新θ的那一步就是maximization，因为我们想要最好的θ。

用稍微数学一点的语言描述一下这个过程

在前文的时候我提到，类似这种知道数据讨论参数的情况，我们可以用最大似然函数对其进行建模，假设是针对参数θ的最大似然函数图像：

因为我们是在讨论参数θ的合理性，想要找到一个最佳的θ，所以这个最大似然函数的一定是关于θ的。这样的函数存在一个问题，他可能不是凸函数，在优化问题上，我们知道凸函数它一定是有一个全局最优解的，但是如果是非凸，那么可能存在多个局部最优解，不是很好进行优化。对于图中的这个函数如何来找到最佳的θ呢? 还是以爬山的那个场景来类比。我既然不知道哪个θ是最好的，我可以随机的初始化一个θ呀，就像随机把人放在山的某个位置一样。就像下图所示，我随机的初始化了一个θ1：
现在的问题是怎么让这个θ向上爬呢？既然我们知道凸函数一定有一个全局最优解，那为什么不利用起来呢？现在我创建一个简单的凸函数g（图中绿色表示的曲线）, 使这个函数g的交于θ1，并且保证g(θ1)的极大值要小于L(θ1)的极小值，其实就是要保证创建的函数g 要在L 下方。上述过程用图像画出来差不多，如下图所示：

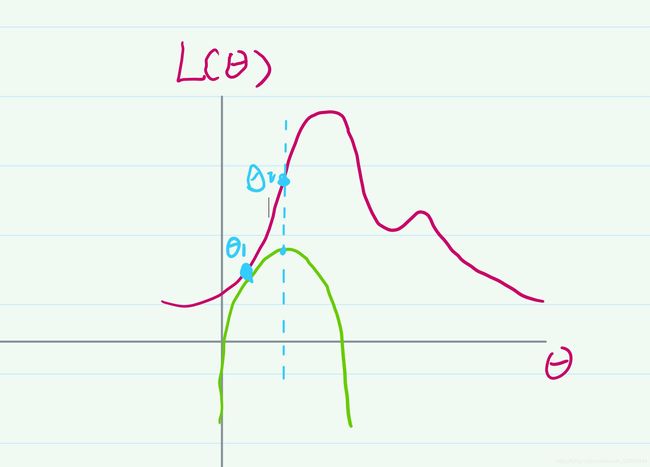
那么凸函数g的最大值是很容易求的。这个时候我们可以把这个凸函数g的全局最优解所对应的那个θ值作为新的θ的值，我将其记为θ2。这个时候可以发现θ已经向上爬了。我们可以对上述步骤进行迭代，在针对θ2创建一个凸函数g2并得到θ3的值，我们可以得到如下图像：

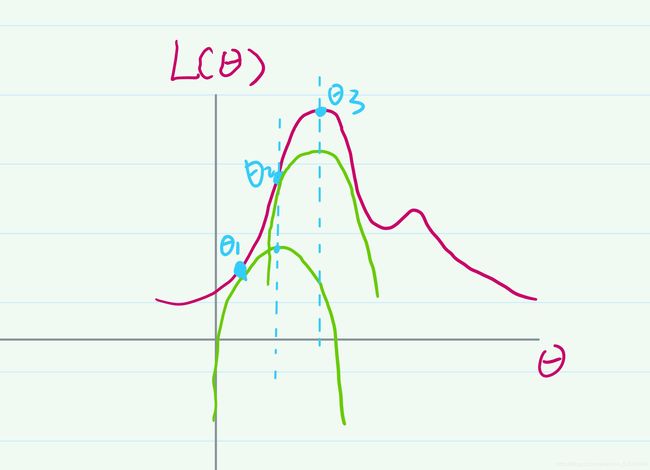
上述步骤一直迭代进行，直到找到一个θ值能最大化这个最大似然函数。也就是找到‘山顶’为止。

数学推导EM算法
在理解EM的数学推导过程之前，首先要理解一个很重要的概念那就是Jensen’s inequality（琴生不等式）。
他可以被定义成：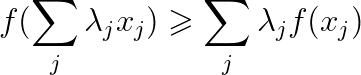
这里的 f 是一个凸函数， $\lambda$ 是指的一种概率分布。那应该如何来理解这一个不等式呢？我们可以先假设目前就只有两个$\lambda$ 和两个$x_j$的情况就比较好理解了。
我们设${\lambda }_1=t$，那么就应该是${\lambda }_2=1-t$，因为一个概率分布中所以的概率相加应该是1嘛。 同时也假设我们有两个变量$x_1$和$x_2$然后将我们所假设好的变量带回到上述的不等式中我们可以得到以下式子：

$f((1-t)x_1+t{x}_2)⩾(1-t)f(x_1)+tf(x_2)$

这样乍一看还是觉得没有感觉。但是至少要意识到，不等式的左边是一条曲线，而右边是一条直线。那么我们要是把图画出来就会清晰很多了。假设这里的这个凸函数是长图里这个样子的：
这样子就很容易理解这个大于等于号是怎么来的了，如果在$x_1$和$x_2$之间随意取一点$x_T$那么这个点所对应的值永远小于那个凸函数,取到段直线两个端点的时候等号成立，正如下图所示：

那么上面这一切和EM算法有什么关系吗？
假设我们有一组独立的数据集{x1,x2,…},我们希望使用一个模型来拟合它，我们可以将这个模型写成下面这个似然函数，这里的 X 就像是我们在第二个投硬币例子里的投掷结果，θ就像是硬币A和B 出现正面的概率。

为什么要取log呢？我的理解是为了方便数学运算，而且取log是不会影响寻找最大值的。
但是上述公式没有把隐变量对结果的影响表达出来，所以我们想办法把隐变量塞进我们的模型中。为了方便理解我将公式拆开来记录。正如前文提到，对于一个投掷结果，它可能是硬币A产生的，也有可能是B产生的，所以我们应该把这个两种情况的概率加在一起:

这里的大Z指的就是隐变量有多少种情况。对于投硬币那个情况而言，就是大Z等于2。所以新的模型可以表达成：

做到这里再来看看当前这个模型离Jensen‘s inequality 还差点啥？？ 是不是只差一个概率分布了？？那在我们已知的条件中还有什么是概率分布呢？？结合抛硬币的例子来看，只有隐变量z的分布Q了呀！！那为了保持等式的值不变，我在等式的右边同时除以和乘以一个$Q(z_j)$得到以下这个等式：

现在上述这个等式就完全和Jensen’s inequality 的形式一致了 (log函数本身就是一个凸函数哦！) 。所以就可以表示成Jensen‘s inequality的形式：

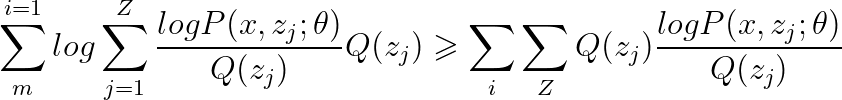
上述不等式在什么情况况下取等号呢？在$log\frac{x,z_j;\theta }{Q(z_j}$等于一个常数的时候等号成立。