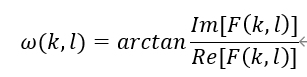opencv显示图像的频谱图(C++)
opencv显示图像的频谱图(C++)
- 1. 图像傅里叶变换
- 2. 幅度谱
- 3.相位谱
- 4. 测试
1. 图像傅里叶变换
图像的傅里叶变换是二维的傅里叶变换,二维离散傅里叶变换(discrete Fourier transform,DFT)定义式如下:
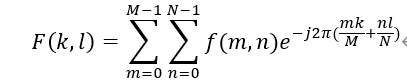
在这里 f ( m , n ) f(m,n) f(m,n)为图像在点 ( i , j ) (i,j) (i,j)的像素值。
二维离散傅里叶反变换为:

在opencv中可以通过dft()函数实现二维离散傅里叶变换,代码如下:
Mat DFT::dft2(Mat input)
{
if (input.channels() != 1) {
std::cout << "只处理单通道的图像" << std::endl;
exit(0);
}
Mat src = input.clone();
//扩充图像尺寸为DFT的最佳尺寸
Mat padded;
int newRows = getOptimalDFTSize(src.rows);
int newCols = getOptimalDFTSize(src.cols);
copyMakeBorder(src, padded, newRows - src.rows, 0, newCols - src.cols, 0, BORDER_CONSTANT, Scalar(0));
//将planes融合合并成一个多通道数组
Mat plans[] = {
Mat_<double>(padded),Mat::zeros(padded.size(),CV_64F) };
Mat mergeArray;
merge(plans, 2, mergeArray);
//傅里叶变换
dft(mergeArray, mergeArray);
return mergeArray;
}
在进行DFT时,特定大小的尺寸会使DFT变换得到更高的处理效率,所以代码中使用getOptimalDFTSize和copyMakeBorder将图像尺寸扩展为适合的尺寸;另外傅里叶变换的结果是复数,需要一个二通道的Mat对象来存储其实部与虚部,所以代码中使用merge将planes融合合并成一个多通道数组。
2. 幅度谱
幅度谱表示为:
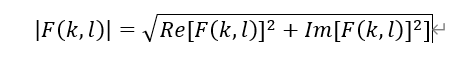
其中 R e [ F ( k , l ) ] Re[F(k,l)] Re[F(k,l)]和 I m [ F ( k , l ) ] Im[F(k,l)] Im[F(k,l)]分别表示 F ( k , l ) F(k,l) F(k,l)的实部和虚部。
在opencv中提供了magnitude可以直接计算幅度。
opencv计算幅度谱并显示:
static void plotMagnitude(Mat input, String imgName,int flag=WINDOW_NORMAL);
void DFT::plotMagnitude(Mat input,String imgName,int flag)//画出幅度谱
{
//imgName是对幅度谱图像取的名字
Mat mergeArray = dft2(input);
Mat plans[2];
//将傅里叶变换结果的实部和虚部分开
split(mergeArray, plans);
//计算幅度,结果存在plans[0]
magnitude(plans[0], plans[1],plans[0]);
//进行对数变换
Mat logArray = plans[0];
logArray += Scalar::all(1);//加1,保证对数有意义
log(logArray, logArray);
//将幅度谱剪裁为偶数行与偶数列(方便后面的重新排列)
logArray = logArray(Range(0, logArray.rows & -2), Range(0, logArray.cols & -2));
//重新排列幅度谱的区域,使得幅度谱的原点位于图像中心
int x0 = logArray.cols / 2;
int y0 = logArray.rows / 2;
Mat q0(logArray, Rect(0, 0, x0, y0)); //左上角图像
Mat q1(logArray, Rect(x0, 0, x0, y0)); //右上角图像
Mat q2(logArray, Rect(0, y0, x0, y0)); //左下角图像
Mat q3(logArray, Rect(x0, y0, x0, y0)); //右下角图像
swapArea(q0, q3);
swapArea(q1, q2);
//归一化,用0-1之间的浮点数将矩阵变换为可视的图像格式
normalize(logArray, logArray, 0, 1, NORM_MINMAX);
namedWindow(imgName, flag);
imshow(imgName, logArray);
}
其中的swapArea的定义如下:
void DFT::swapArea(Mat& area1, Mat& area2)
{
Mat temp;
area1.copyTo(temp);
area2.copyTo(area1);
temp.copyTo(area2);
}
代码的几点解释:
- 由于傅里叶变换计算出来的幅度值范围一般比较大,会导致小的幅度值变成黑点,而大的幅度值变成白点,所以进行对数变换,压缩高值,拉伸低值(也就是增强对比度算法中的对数变换)。
- 由于图像傅里叶变换后的原点在图像的左上角,为了使得幅度谱的原点位于图像中心,便于观察,代码中将图像的四个区域(q0,q1,q2,q3)重新排列。排列方式如下图:

- 为了方便上面的重新排列,我们将幅度谱剪裁为偶数行与偶数列。英文int型的负数在计算机中的存储是以补码表示的,因此-2在计算机中存储为: ( 11111111111111111111111111111110 ) B (1111 1111 1111 1111 1111 1111 1111 1110)_B (11111111111111111111111111111110)B,所以当一个数与他进行位与时,如果是偶数,则不发生改变,如果是奇数,则相当于减去1,变成偶数。
- 我们现在得到的幅度值仍然超出了0-1的显示范围,所以需要对数据进行归一化处理。
3.相位谱
opencv显示相位谱代码:
static void plotPhase(Mat input, String imgName, int flag = WINDOW_NORMAL);
void DFT::plotPhase(Mat input, String imgName, int flag)
{
//imgName是对相位谱图像取的名字
Mat mergeArray = dft2(input);
Mat plans[2] ;
//将傅里叶变换结果的实部和虚部分开
split(mergeArray, plans);
int rows = mergeArray.rows;
int cols = mergeArray.cols;
Mat phaseImg(rows, cols, CV_64F);
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
phaseImg.at<double>(i, j) = atan2(plans[1].at<double>(i, j), plans[0].at<double>(i, j));
}
}
phaseImg = phaseImg(Range( 0, phaseImg.rows & -2),Range(0, phaseImg.cols & -2));
int y0 = phaseImg.rows/2;
int x0 = phaseImg.cols/2;
Mat q0(phaseImg, Rect(0, 0, x0, y0)); //左上角图像
Mat q1(phaseImg, Rect(x0, 0, x0, y0)); //右上角图像
Mat q2(phaseImg, Rect(0, y0, x0, y0)); //左下角图像
Mat q3(phaseImg, Rect(x0, y0, x0, y0)); //右下角图像
swapArea(q0, q3);
swapArea(q1, q2);
normalize(phaseImg, phaseImg, 0, 1, NORM_MINMAX);
namedWindow(imgName, flag);
imshow(imgName, phaseImg);
}
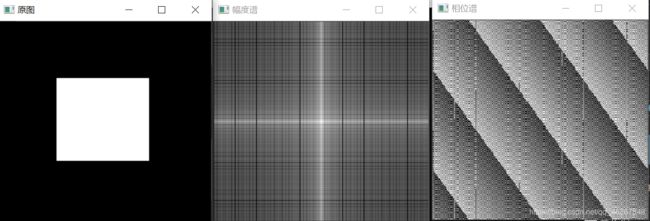
4. 测试
幅度谱与相位谱测试代码:
#include