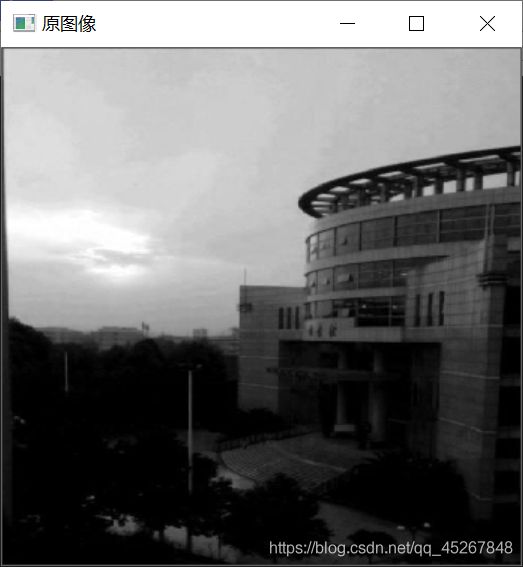
对比度增强算法
目录
- 1、线性变换增强对比度
-
- 1.1、简单线性变换
- 1.2、分段线性变换
- 2、非线性变换增强对比度
-
- 2.1、对数变换
- 2.2、指数变换( γ \gamma γ矫正)
- 3、其他变换
-
- 3.1、灰度切片
- 3.2、图像求反
- 3.3、位图分割
1、线性变换增强对比度
1.1、简单线性变换
如果原图像 f ( x , y ) f(x,y) f(x,y)的灰度范围为 [ m , M ] [m,M] [m,M],经过线性变换之后，我们希望变换后的图像 g ( x , y ) g(x,y) g(x,y)的灰度范围是 [ n , N ] [n,N] [n,N],那么经过下面的简单线性变换就可实现：
g ( x , y ) = ( N − n ) / ( M − m ) [ f ( x , y ) − m ] + n g(x,y)=(N-n)/(M-m) [f(x,y)-m]+n g(x,y)=(N−n)/(M−m)[f(x,y)−m]+n
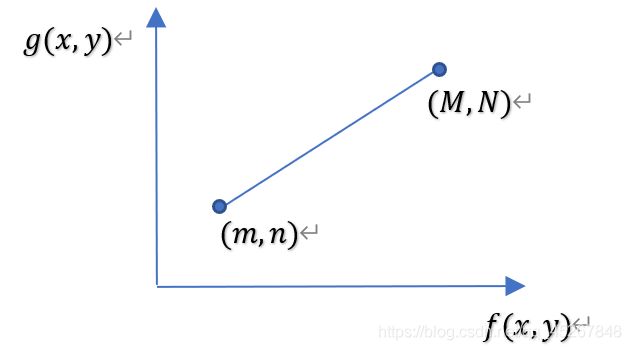
图1. 简单线性变换关系曲线
令系数 k = ( N − n ) / ( M − m ) k=(N-n)/(M-m) k=(N−n)/(M−m)，则 k k k的不同，处理的效果也不同。
当 0 < k < 1 0
当 k = 1 k=1 k=1的时候，图像的灰度范围没变，但是灰度区间可能发生平移；
当 k > 1 k>1 k>1时，图像的灰度范围变大，常常能够更凸显细节。
当 k < 0 k<0 k<0时，图像的灰度反转，即亮部分变成暗的部分，暗部分又变成亮的部分，在本文图像求反部分还将考虑。
此处考虑一个简单情况（n=0，k=1/0.6），代码如下：
#include将像素值限制在0~255
}
}
imshow("简单线性变换后的图像", dstImage);
waitKey(0);
return 0;
}
执行效果：
经过简单线性变换后，图像变亮，对比度有所提高。
1.2、分段线性变换
分段线性变换是常用的线性变换。仍以 f ( x , y ) f(x,y) f(x,y)表示变换前的图像， g ( x , y ) g(x,y) g(x,y)表示变换后的图像，则变换关系为：
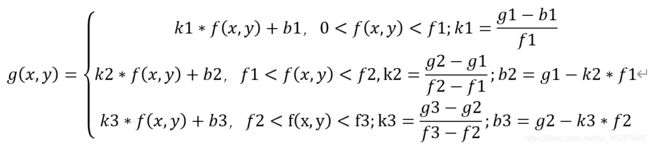
图2.分段线性变换关系曲线
如果令 k 1 < 1 , k 3 < 1 , k 2 > 1 k1<1,k3<1,k2>1 k1<1,k3<1,k2>1，则这种变换使得灰度值在 [ 0 , f 1 ] [0,f1] [0,f1]和 [ f 2 , f 3 ] [f2,f3] [f2,f3]中的像素值被压缩，而 [ f 1 , f 2 ] [f1,f2] [f1,f2]的像素值被扩展。也就是说压缩过亮或过暗的像素，扩展亮度适中的像素。因为人眼在亮度适中的情况下更容易区分细节，所以可以改变图像的视觉效果。
简单修改简单线性变换的代码即可实现分段线性变换功能：
#include将像素值限制在0~255
}
}
imshow("简单线性变换后的图像", dstImage);
waitKey(0);
return 0;
}
执行效果：
其实如果图像在黑色或白色附近（像素值较低或较高）存在干扰，那么使用分段线性变换可以使人眼对干扰感受不明显，从而改善图像的视觉效果。
2、非线性变换增强对比度
原理上来说的话，非线性变换是由非线性函数变换而来，自然会有很多变换方法，但较多使用的是对数变换和指数变换。
2.1、对数变换
对数变换的表达式为：
g ( x , y ) = C ∗ l n ( f ( x , y ) + 1 ) g(x,y)=C*ln(f(x,y)+1) g(x,y)=C∗ln(f(x,y)+1)
图3.对数变换曲线示意图
C C C为常数，用于使变换后的图像 g ( x , y ) g(x,y) g(x,y)的灰度值的范围符合要求。
代码实现：
#include对数变换效果图:
图像经过对数变换后相当于低灰度值被扩展，而高灰度值被压缩，这就使得低灰度值的图像细节更容易看清。图像红圈处低灰度值区域经过对数变换后的确更能分辨细节。
2.2、指数变换( γ \gamma γ矫正)
用于图像获取、显示、打印的许多装置的响应往往是指数响应。设 f f f为图像的灰度值， s s s为CCD图像传感器或胶片等的入射光强度，则输入光强度与输出信号之间的关系为：
f = c s γ f=cs^γ f=csγ
其中， c c c为常数， γ \gamma γ值表示摄像装置的特性，在同一装置中 γ \gamma γ值是确定的。当 γ < 1 \gamma<1 γ<1时，低灰度区间扩展而高灰度区间压缩，当 γ > 1 \gamma>1 γ>1则相反。
为了使得变换后的图像与入射光的强度相等或成正比，我们可以进行 γ \gamma γ校正，即：
g = ( f / c ) ( 1 / r ) g=(f/c)^(1/r) g=(f/c)(1/r);
我们这里取 c = 25 5 ( 1 − γ ) c=255^(1-\gamma) c=255(1−γ)以使像素值能够扩展至0~255，代码如下：
#include利用 γ \gamma γ校正增强灰度图像对比度效果：
3、其他变换
3.1、灰度切片
灰度切片是将某一范围的灰度取出，转换成较大的灰度加以显示，突出我们感兴趣的灰度在图像中的分布情况。其灰度曲线如下图：
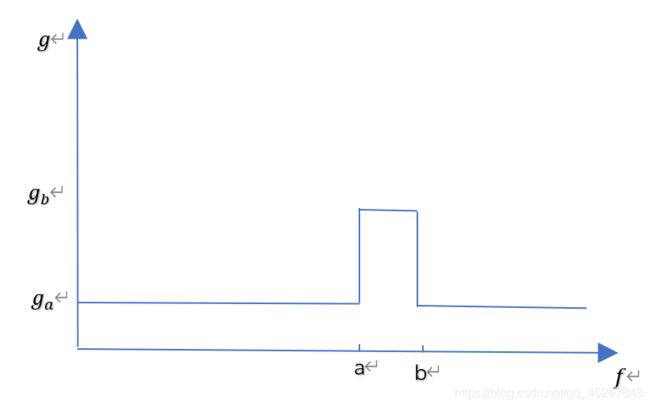
图4.灰度切片变换曲线
实现代码（此处取 a = 150 , b = 200 , g a = 0 , g b = 150 , b = 250 a=150,b=200,ga=0,gb=150,b=250 a=150,b=200,ga=0,gb=150,b=250）：
#include灰度切片效果：
可见其中一些灰度被突出
3.2、图像求反
图像求反实际上就是简单线性变换中 k < 0 k<0 k<0的情况，它能起到帮我们发现暗部细节的作用。
我们这里令变换关系式为 g ( x , y ) = − f ( x , y ) + 255 g(x,y)=-f(x,y)+255 g(x,y)=−f(x,y)+255，代码如下：
#include图像求反效果图：
3.3、位图分割
位图分割即对图像像素的特定位进行操作来实现。比如图像量化为8比特，那么图像就可以由8个1比特的平面组成，其范围从最低有效位的位平面0到最高有效位的位平面7。在8比特的字节中，位平面0包含图像中像素的最低位，而平面7则包含最高位。就8比特图像的位平面抽取。
就8比特图像的位平面抽取而言，如果获取位平面7的二值图像，可以通过以下步骤：
（1）把图像中0~127间的所有灰度映射到一个灰度值（如0）
（2）把图像128~255间的灰度映射为令一种灰度值（如255），其他位面图的获取以此类推。
代码如下：
#include位平面效果图：
可以看出较高阶位面包含了大部分视觉上很重要的轮廓信息。