图像平滑
目录
- 1. 噪声
- 2. 邻域平均法
-
- 2.1. 简单平均法
- 2.2. 灰度差值门限法
- 2.3. 加权平均法
- 3. 多图平均法
- 4. 中值滤波法
- 5. 高斯滤波
- 6. opencv的平滑处理函数
- 7. 总结
1. 噪声
图像在获取的过程中一般会受到各种干扰而导致图像含有噪声。噪声的产生原因有很多,噪声产生的原因决定了噪声的分布特性。
当噪声 n ( x , y ) n(x,y) n(x,y)与图像信号 g ( x , y ) g(x,y) g(x,y)无关时,含噪图像 f ( x , y ) f(x,y) f(x,y)可以用下面的式子表示:
f ( x , y ) = g ( x , y ) + n ( x , y ) f(x,y)=g(x,y)+n(x,y) f(x,y)=g(x,y)+n(x,y)
这种噪声称作加性噪声。
还有一种乘性噪声,即噪声和信号有关,含噪图像 f ( x , y ) f(x,y) f(x,y)表示为:
f ( x , y ) = g ( x , y ) + n ( x , y ) g ( x , y ) = [ 1 + n ( x , y ) ] g ( x , y ) = n 1 ( x , y ) g ( x , y ) f(x,y)=g(x,y)+n(x,y)g(x,y)=[1+n(x,y)]g(x,y)=n_1(x,y)g(x,y) f(x,y)=g(x,y)+n(x,y)g(x,y)=[1+n(x,y)]g(x,y)=n1(x,y)g(x,y)
对于大多数传感器,与信号一起产生的噪声可以模拟为高斯分布和泊松分布的随机过程。高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声。因为后面会用到高斯噪声,这里利用opencv给图像加上高斯噪声。
利用Box-Muller 算法可以算出一个正态分布的随机数字 Z,具体方法百度如下:
算出正态分布的随机数字 Z之后,就可以给图像加上高斯噪声了,算法的关键程序代码如下:
Mat addNoise::addGaussianNoise(Mat src)
{
Mat dst = src.clone();
int ncols = dst.cols*dst.channels();
int rows = dst.rows;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < ncols; j++) {
dst.at<uchar>(i, j) =saturate_cast<uchar>(dst.at<uchar>(i,j)+ (uchar)generateGuassianNumber());
}
}
return dst;
}
double addNoise::generateGuassianNumber()
{
double u1 = (double)rand() / RAND_MAX;
double u2 =(double) rand() / RAND_MAX;
double R = sqrt(-2 * log(u1));
double theta = 2 * M_PI * u2;
return R*cos(theta);
}
2. 邻域平均法
邻域平均法在空间域平滑噪声。对于给定NXN个像素的数字图像 [ f ( i , j ) ] [f(i,j)] [f(i,j)]的每个像素点 ( m , n ) (m,n) (m,n),取其邻域S,若S中含有M个像素,以平均值
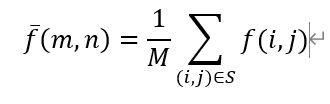
代替原像素点的灰度值。
设含噪图像 f f f在像素点 ( i , j ) (i,j) (i,j)为: f ( x , y ) = g ( x , y ) + n ( x , y ) f(x,y)=g(x,y)+n(x,y) f(x,y)=g(x,y)+n(x,y)
经过邻域平均后的图像为:
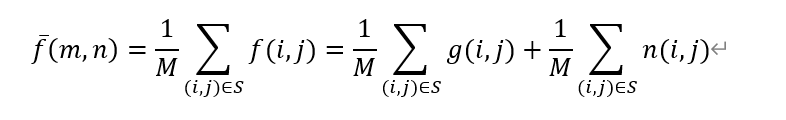
若噪声在空间上不相关,其期望为零,方差为 σ 2 \sigma^2 σ2,则处理后噪声期望为零,方差为 σ 2 / M \sigma^2/M σ2/M,可见方差变小了,说明噪声强度减弱了,即抑制了噪声。由上式也可以看出邻域平均法在消弱噪声的同时也平滑了图像,可能导致目标边界变得不清晰。
2.1. 简单平均法
设S为3X3邻域,点 ( m , n ) (m,n) (m,n)位于S的中心,则:
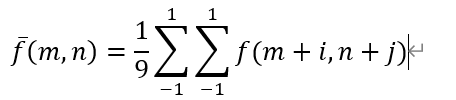
对于其他邻域处理与上式类似。
测试代码如下:
#include 其中的ImageSmoothing::simpleAvg定义如下:
Mat ImageSmoothing::simpleAvg(Mat input, int s1 , int s2 )
{
/*
简单平均法,s1,s2为邻域S大小
s1,s2只能输入奇数
*/
if (s1 % 2==0 || s2 % 2==0) {
std::cout << "参数s1,s2请输入奇数" << std::endl;
exit(0);
}
Mat src = input.clone();
/*
由于mat的值传递不另开辟实例空间
为了处理之后的图像不改变原图像,这里克隆一下
*/
int rows = src.rows;
int cols = src.cols;
int channels = src.channels();
Mat dst(src.size(), src.type(),Scalar(0));
int S = s1 * s2;
int i0 = (s1 - 1) / 2;
int j0 = (s2 - 1) / 2;
for (int m = i0; m < rows - i0; m++) {
for (int n =j0*channels; n < (cols - j0 )* channels; n++) {
for (int i = -i0; i <= i0; i++) {
for (int j = -j0; j <= j0; j++) {
dst.at<uchar>(m, n) += (src.at<uchar>(m + i, n + j * channels)/S);
}
}
}
}
return dst;
}
测试结果:
由测试结果可见平滑窗口越大,去噪效果越好,但是对图像的伤害也越大。
2.2. 灰度差值门限法
由于受噪干扰的像素的灰度和相邻像素差别较大,灰度差值门限法即选取一适当的门限,当某个像素点的灰度与邻域平均值之差大于这个门限T时,就令这一点的像素等于灰度平均值,否则为原灰度。公式如下:
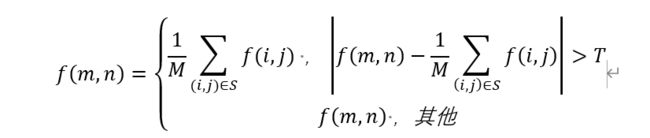
这种方法可以把较大的噪声滤除,而对信号影响不大。
算法的关键程序代码如下:
static Mat grayDT(Mat input, int s1=3, int s2=3,uchar T=50);
Mat ImageSmoothing::grayDT(Mat input, int s1, int s2, uchar T)
{
//灰度差值门限法
if (s1 % 2 == 0 || s2 % 2 == 0) {
std::cout << "参数s1,s2请输入奇数" << std::endl;
exit(0);
}
Mat src = input.clone();
int rows = src.rows;
int cols = src.cols;
int channels = src.channels();
Mat dst(src.size(), src.type(), Scalar(0));
int S = s1 * s2;
int i0 = (s1 - 1) / 2;
int j0 = (s2 - 1) / 2;
for (int m = i0; m < rows - i0; m++) {
for (int n = j0 * channels; n < (cols - j0) * channels; n++) {
for (int i = -i0; i <= i0; i++) {
for (int j = -j0; j <= j0; j++) {
dst.at<uchar>(m, n) += (src.at<uchar>(m + i, n + j * channels) / S);
}
}
if (abs(dst.at<uchar>(m, n) - src.at<uchar>(m, n)) <= T) {
dst.at<uchar>(m, n) = src.at<uchar>(m, n);
}
}
}
return dst;
}
灰度差值门限法平滑噪声效果:
可以看出这种方法比单纯使用简单平均法更能保护图像信息
2.3. 加权平均法
当处理图像内部区域的边界点时,由于边界点与周围的反差较大,那么邻域平均法处理后边界点必然会变得模糊,为了解决这个问题,,可采用加权平均法,即根据参与平均像素的特点赋予不同的权值。下面实现两种常见的加权算子。
中心加权算子以及中心和四邻点加权算子是常见的两种算子,其中:
中心加权算子:
1 / 10 [ 1 1 1 1 2 1 1 1 1 ] 1/10\begin{bmatrix} 1&1&1\\ 1&2&1\\ 1&1&1 \end{bmatrix} 1/10⎣⎡111121111⎦⎤
中心和四邻点加权算子:
1 / 16 [ 1 2 1 2 4 2 1 2 1 ] 1/16\begin{bmatrix} 1&2&1\\ 2&4&2\\ 1&2&1 \end{bmatrix} 1/16⎣⎡121242121⎦⎤
算法的关键程序代码如下:
Mat ImageSmoothing::weightedAvg(Mat input, Array<double> w)//加权平均法
{
Mat src = input.clone();
int imgRows = src.rows;
int imgCols = src.cols;
int channels = src.channels();
Mat dst(src.size(), src.type(),Scalar(0));
int wRows = w.getRows();
int wCols = w.getCols();
int i0 = wRows / 2;
int j0 = ((int)(wCols /2))* channels ;
for (int i =i0; i < imgRows -i0; i++) {
for (int j = j0; j < imgCols * channels - j0; j++) {
for (int m = 0; m < wRows; m++) {
for (int n = 0; n < wCols; n++) {
dst.at<uchar>(i, j) +=
(w.getItem(m, n) * src.at<uchar>(i - i0 + m , j - j0 + n * channels));
}
}
}
}
return dst;
}
其中的Array类是自定义的类,定义如下:
#include 对以上两种算子的测试代码如下:
#include 加权平均平滑图像的效果:
可以看出这种方法比简单的平均效果要好,对图像的损害相对较小。
3. 多图平均法
以 f m f_m fm表示参与平均的第 m m m幅图片,则多图平均后的图片在像素点 ( i , j ) (i,j) (i,j)处的灰度值为:

假设图像 g g g受到噪声 n n n的干扰,则受干扰图像 f m f_m fm在像素点 ( i , j ) (i,j) (i,j)处的灰度值为:
f m ( i , j ) = g ( x , y ) + n m ( i , j ) f_m(i,j)=g(x,y)+n_m(i,j) fm(i,j)=g(x,y)+nm(i,j)
多图平均后的图片在像素点 ( i , j ) (i,j) (i,j)处的灰度值为:
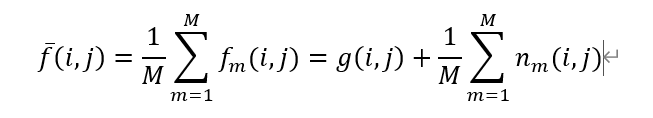
噪声的期望值为0,方差为 σ 2 \sigma^2 σ2,则多图平均后期望仍为0,但方差变为 σ 2 / M \sigma^2/M σ2/M,而图像信号仍为 g g g,并未被平滑,从而达到了抑制噪声的效果。参与平均的图像数目越多,消减噪声的效果越好,当参与平均的图像数目趋于无穷大时,噪声也就趋于0。如果能在相同的条件下对同一景物获取若干张图片,多图平均法是不错的选择。
算法的关键程序代码如下:
Mat ImageSmoothing::multImgAvg(Mat* input, int imgNum)//多图平均法
{
//imgNum为输入图像数量
for (int i = 1; i < imgNum; i++) {
if (input[0].size() != input[i].size() || input[0].type() != input[i].type()) {
std::cout << "请输入一样尺寸,一样类型的图片" << std::endl;
exit(0);
}
}
Mat dst(input[0].size(),input->type(),Scalar(0));
int rows = input[0].rows;
int cols = input[0].cols;
int channels = input[0].channels();
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols * channels; j++) {
double val = 0;
for (int k = 0; k < imgNum; k++) {
val +=(double) input[k].at<uchar>(i,j) / imgNum;
}
dst.at<uchar>(i, j) = (uchar)val;
}
}
return dst;
}
测试程序代码如下:
#include 测试效果:
如果愿意等,用100张受干扰图片进行平均,发现平均后的图基本和原图是一样的。
4. 中值滤波法
由于噪声相对于周围的像素反差较大,含噪的像素一般不是偏亮就是偏暗。如果把一个邻域内的像素点按大小进行排序,如果存在噪声,那么噪声点肯定在排序后的序列的两端,此时取中间值进行输出,就可以消除噪声的影响,这就是中值滤波的思想。
所谓中值滤波就是存在一个确定的领域A,规定图像中值滤波后某像素点的输出等于该像素点邻域中各像素值的灰度的中值。阵列 [ x ( i , j ) ] [x(i,j)] [x(i,j)]经过窗口 A n A_n An中值滤波后,像素点 ( i , j ) (i,j) (i,j)的输出记为:
y ( i , j ) = m e d [ x ( i , j ) ] y(i,j)=med[x(i,j)] y(i,j)=med[x(i,j)]
算法的关键程序代码如下(取 A n A_n An为矩形窗口):
Mat ImageSmoothing::medBlur(Mat input, int Asize)
{
//Asize为窗口大小(正方形)
Mat src = input.clone();
int imgRows = src.rows;
int imgCols = src.cols;
int channels = src.channels();
Mat dst(src.size(), src.type(), Scalar(0));
int i0 = Asize / 2;
int j0 = i0*channels;
for (int i =i0; i < imgRows-i0; i++) {
for (int j = j0; j <( imgCols-j0)* channels; j++) {
Mat arr(1,Asize*Asize, CV_8UC1);
for (int m = 0; m < Asize;m++) {
for (int n = 0; n < Asize; n++) {
arr.at<uchar>(0,m*Asize+n) = src.at<uchar>(i - i0 + m, j - j0 + n * channels);
}
}
sort(arr, arr,0);
if (Asize % 2) {
dst.at<uchar>(i, j) = arr.at<uchar>(0, Asize * Asize / 2);
}
else {
dst.at<uchar>(i, j) =(uchar)( (int)(arr.at<uchar>(0, Asize * Asize / 2)+ arr.at<uchar>(0, (Asize * Asize / 2)-1))/2);//Asize偶数时取中间两个平均值
}
}
}
return dst;
}
测试代码如下:
#include 中值滤波与均值滤波对比
可以看出中值滤波效果比均值滤波好,同时中值滤波也会随着滤波窗口的增大,而对图像损害越来越大
5. 高斯滤波
图像大多数噪声均属于高斯噪声,因此高斯滤波器应用也较广泛。
高斯滤波去噪就是对整幅图像像素值进行加权平均,针对每一个像素点的值,都由其本身值和邻域内的其他像素值经过加权平均后得到。
高斯滤波在空间域的处理方法关键就是确定高斯核,所谓高斯核,就是根据根绝高斯分布函数确定的加权算子,也就是说高斯滤波是一种特殊的加权平均法。
一维高斯分布:
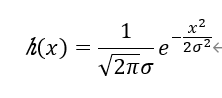
二维高斯分布:

以3以下3X3的高斯核为例:
[ h ( − 1 , − 1 ) h ( − 1 , 0 ) h ( − 1 , 1 ) h ( 0 , − 1 ) h ( 0 , 0 ) h ( 0 , 1 ) h ( 1 , − 1 ) h ( 1 , 0 ) h ( 1 , 1 ) ] \begin{bmatrix} h(-1,-1)&h(-1,0)&h(-1,1)\\ h(0,-1)&h(0,0)&h(0,1)\\ h(1,-1)&h(1,0)&h(1,1) \end{bmatrix} ⎣⎡h(−1,−1)h(0,−1)h(1,−1)h(−1,0)h(0,0)h(1,0)h(−1,1)h(0,1)h(1,1)⎦⎤
将各个位置的坐标带入到高斯分布函数中,则可以确定 h ( i , j ) h(i,j) h(i,j),比如:(以 σ = 0.8 \sigma=0.8 σ=0.8为例)
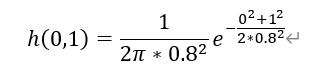
对于高斯核的大小为 (2k+1)×(2k+1)的窗口,窗口中各个元素值的计算公式如下:
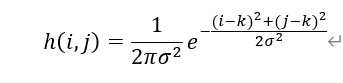
算法的关键程序代码如下:
Mat ImageSmoothing::guassianBlur(Mat inputImg, int templeSize, double sigma)
{
//高斯滤波
if (templeSize % 2 == 0) {
std::cout << "只处理奇数尺寸的模板窗口" << std::endl;
exit(0);
}
Mat src = inputImg.clone();
int k = templeSize / 2;
Array<double> H(templeSize, templeSize);
double sigma2 = sigma * sigma;
for (int i = 0; i < templeSize; i++) {
for (int j = 0; j < templeSize; j++) {
double data = exp(-(pow(i-k,2)+pow(j-k,2))/(2*sigma2))/(2*M_PI*sigma2);
H.addItem(data, i, j);
}
}
Mat dst = weightedAvg(src,H);//高斯滤波是特殊的加权平均法
return dst;
}
高斯滤波效果:
在高斯滤波中标准差代表着数据的离散程度,如果 σ \sigma σ较小,那么生成的高斯核的中心系数较大,而周围的系数较小,这样对图像的平滑效果就不是很明显;反之, σ \sigma σ较大,则生成的高斯核的各个系数相差就不是很大,比较类似均值滤波,对图像的平滑效果比较明显
6. opencv的平滑处理函数
上面图像平滑所涉及的滤波方法,在opencv中都是直接提供了相关函数的。下面使用分别使用blur(),medianBlur(),GaussianBlur进行均值滤波,中值滤波以及高斯滤波。
#include 效果如下:
7. 总结
图像平滑能够平滑掉图像噪声,图像平滑操作除了上述方法外,还包括很多处理方法,比如双边滤波法,频率域处理等。