1.7 Linear independence (线性无关)

本文为《Linear algebra and its applications》的读书笔记

Definition

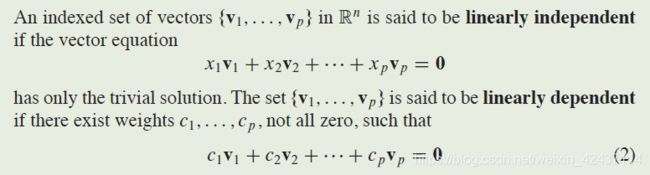
Equation (2) is called a linear dependence relation (线性相关关系) among { ${\mathbf{v}}_1,...,{\mathbf{v}}_p$} when the weights are not all zero. For brevity, we may say that ${\mathbf{v}}_1,...,{\mathbf{v}}_p$ are linearly dependent when we mean that { ${\mathbf{v}}_1,...,{\mathbf{v}}_p$} is a linearly dependent set. We use analogous terminology for linearly independent sets.

Linear Independence of Matrix Columns

Suppose that we begin with a matrix $A=[{\mathbf{a}}_1,...,{\mathbf{a}}_n]$ instead of a set of vectors. The matrix equation $A\mathbf{x}=0$ can be written as
$$x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+...+x_n{\mathbf{a}}_n=0$$ The columns of a matrix $A$ are linearly independent if and only if the equation $A\mathbf{x}=0$ has only the trivial solution.

注意：这里的线性相关/无关是针对矩阵的列，而非矩阵本身而言的。线性相关/无关的概念用于向量而非矩阵
The columns of a matrix may be linearly independent, but it is meaningless to refer to a linearly independent matrix.

Sets (集合) of One or Two Vectors

A set containing only one vector—say, $\mathbf{v}$—is linearly independent if and only if $\mathbf{v}$ is not the zero vector. This is because the vector equation $x_1\mathbf{v}=0$ has only the trivial solution when $\mathbf{v}\ne 0$.

The next example will explain the nature of a linearly dependent set of two vectors

EXAMPLE 3
Determine if the following sets of vectors are linearly independent.

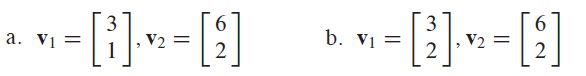
SOLUTION
a. Notice that ${\mathbf{v}}_2$ is a multiple of ${\mathbf{v}}_1$. Hence $-2{\mathbf{v}}_1+{\mathbf{v}}_2=0$, which shows that { ${\mathbf{v}}_1$,${\mathbf{v}}_2$} is linearly dependent.
b. The vectors ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ are certainly not multiples of one another. Could they be linearly dependent? Suppose $c$ and $d$ satisfy
$$c{\mathbf{v}}_1+d{\mathbf{v}}_2=0$$If $c\ne 0$, then we can solve for ${\mathbf{v}}_1$ in terms of ${\mathbf{v}}_2$, namely, ${\mathbf{v}}_1=(-d/c){\mathbf{v}}_2$. This result is impossible because ${\mathbf{v}}_1$ is not a multiple of ${\mathbf{v}}_2$. So $c$ must be zero. Similarly, $d$ must also be zero. Thus { ${\mathbf{v}}_1$,${\mathbf{v}}_2$} is a linearly independent set.

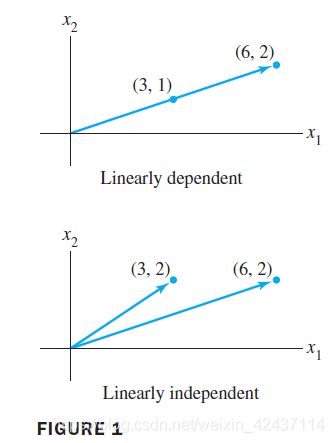
The arguments in Example 3 show that you can always decide by $inspection$ when a set of two vectors is linearly dependent. Row operations are unnecessary.

A set of two vectors { ${\mathbf{v}}_1$,${\mathbf{v}}_2$} is linearly dependent if at least one of the vectors is a multiple of the other.
The set is linearly independent if and only if neither of the vectors is a multiple of the other.

EXAMPLE 判断题
If ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ are in ${\mathbb{R}}^4$ and ${\mathbf{v}}_2$ is not a scalar multiple of ${\mathbf{v}}_1$, then { ${\mathbf{v}}_1$,${\mathbf{v}}_2$} is linearly independent.
SOLUTION
False. ${\mathbf{v}}_1$ can be $0$.

Sets of Two or More Vectors

$Warning$: Theorem 7 does not say that $every$ vector in a linearly dependent set is a linear combination of the preceding vectors. A vector in a linearly dependent set may fail to be a linear combination of the other vectors.

推论：
Any set { $\mathbf{u},\mathbf{v},\mathbf{w}$} in ${\mathbb{R}}^3$ with $\mathbf{u}$ and $\mathbf{v}$ linearly independent. The set { $\mathbf{u},\mathbf{v},\mathbf{w}$} will be linearly dependent if and only if $\mathbf{w}$ is in the plane spanned by $\mathbf{u}$ and $\mathbf{v}$.

THEOREM 8

(令$A=[{\mathbf{v}}_1,...,{\mathbf{v}}_p]$，因为$p>n$，因此$A$ 中必有自由变量，$A\mathbf{x}=0$ 必有非平凡解)

EXAMPLE 5
The vectors $\left[\begin{array}{c}2\\ 1\end{array}\right]$,$\left[\begin{array}{c}4\\ -1\end{array}\right]$,$\left[\begin{array}{c}-2\\ 2\end{array}\right]$ are linearly dependent by Theorem 8, because there are three vectors in the set and there are only two entries in each vector. Notice, however, that none of the vectors is a multiple of one of the other vectors. See Figure 4.