python3__深度学习：卷积神经网络（CNN）__LeNet5：支票高效手写数字体识别

1.LeNet5基本概念

在计算机视觉中卷积神经网络取得了巨大的成功，在工业上以及商业上的应用非常多，一种商业上最典型的应用就是识别支票上的手写数字的LeNet5神经网络。LeNet5 这个网络虽然很小，但是它包含了深度学习的基本模块：卷积层，池化层，全链接层，是其他深度学习模型的基础。

2.各层参数详解

LeNet-5共有7层，不包含输入，每层都包含可训练参数；每个层有多个特征映射，每个特征映射通过一种卷积滤波器提取输入的一种特征，然后每个特征映射有多个神经元。 

 

2.1 Input输入层

首先是数据 INPUT 层，输入图像的尺寸统一归一化为32*32。

注意：本层不算LeNet-5的网络结构，传统上，不将输入层视为网络层次结构之一。

2.2 C1卷积层

输入图片：32*32（m, n）

卷积核大小：5*5（km, kn）

卷积核种类：6

输出特征映射大小：28*28  <->（32-5+1=28）

神经元数量：6（每一个神经元为大小28*28的特征映射）

可训练参数：（5*5+1) * 6（每个滤波器5*5=25个unit参数和一个bias参数，一共6个滤波器）

连接数：（5*5+1）*6*28*28=122304

详细说明：

对输入图像进行第一次卷积运算（使用 6 个大小为 5*5 的卷积核），得到6个C1特征图（6个大小为28*28的特征映射, m-km+1=28）。我们再来看看需要多少个参数，卷积核的大小为5*5，总共就有6*（5*5+1）=156个参数，其中+1是表示一个核有一个bias。对于卷积层C1，C1内的每个像素都与输入图像中的5*5个像素和1个bias有连接，所以总共有156*28*28=122304个连接（connection）。有“122304”个连接，但是我们只需要学习156个参数，主要是通过权值共享实现的。

2.3 S2池化层（下采样）

输入：28*28

池化窗口大小：2*2

采样种类：6

采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid等函数

输出特征映射大小：14*14（28/2=14）

神经元数量：6

连接数：（2*2+1）*6*14*14

S2中每个特征图的大小是C1中特征图大小的1/4。

详细说明：

第一次卷积之后紧接着就是池化运算，使用 2*2大小的池化窗口对输入进行池化，于是得到了S2，6个14*14的 特征（28/2=14）。S2这个池化层是对C1中的2*2区域内的像素求和乘以一个权值系数再加上一个偏置，然后将这个结果再做一次映射（sigmod等函数）。同时有5x14x14x6=“5880”个连接。

2.4 C3卷积层

输入：S2中“所有6个”或“几个特征映射的组合”（14*14）

卷积核大小：5*5

卷积核种类：16

神经元数量：16

输出的特征映射大小：10*10  <->  (14-5+1=10)

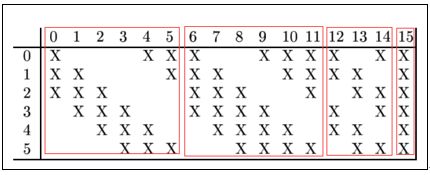
C3中的每个特征映射是连接到S2中的所有6个或者几个特征映射的，表示本层的特征map是上一层提取到的特征map的不同组合；存在的一个方式是：C3的前6个特征图以S2中3个相邻的特征图子集为输入。接下来6个特征图以S2中4个相邻特征图子集为输入。然后的3个以不相邻的4个特征图子集为输入。最后1个将S2中所有特征图为输入。

可训练参数：6*(3*5*5+1)+6*(4*5*5+1)+3*(4*5*5+1)+1*(6*5*5+1)=1516

连接数：10*10*1516=151600

详细说明：

第一次池化之后是第二次卷积，第二次卷积的输出是C3，16个10x10的特征图，卷积核大小是 5*5. 我们知道S2有6个14*14 的特征图，怎么从6 个特征图得到 16个特征图了？ 这里是通过对S2的特征图特殊组合计算得到的16个特征图。具体如下：

 C3的前6个特征映射（对应上图第1个红框的6列）与S2层相连的3个特征映射相连接（上图第1个红框中X对应的行），后面6个特征映射与S2层相连的4个特征映射相连接（上图第2个红框），后面3个特征映射与S2层部分不相连的4个特征映射相连接，最后一个与S2层的所有特征映射相连。卷积核大小依然为5*5，所以总共有6*(3*5*5+1)+6*(4*5*5+1)+3(4*5*5+1)+1*(6*5*5+1)=1516个参数。而图像大小为10*10，所以共有151600个连接。

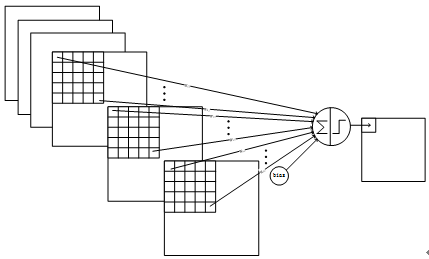
C3与S2中前3个图相连的卷积结构如下图所示： 

上图对应的参数为 3*5*5+1，一共进行6次卷积得到6个特征图，所以有6*（3*5*5+1）参数。 为什么采用上述这样的组合了？论文中说有两个原因：1）减少参数，2）这种不对称的组合连接的方式有利于提取多种组合特征。

2.5 S4池化层（下采样层）

输入：10*10

采样区域：2*2

采样方式：4个输入相加，乘以一个可训练参数，再加上一个可训练偏置。结果通过sigmoid

采样种类：16（C3卷积层输出的特征映射大小）

输出特征映射的大小：5*5（10/2）

神经元数量：16

可训练参数：16（2*2+1）

连接数：16*（2*2+1）*5*5=2000

S4中每个特征图的大小是C3中特征图大小的1/4（25/100=1/4）

详细说明：S4是池化层，窗口大小仍然是2*2，共计16个特征映射，C3层的16个10x10的图分别进行以2x2为单位的池化得到16个5x5的特征图。有16*（2*2＋1）*5*5=2000个连接。连接的方式与S2层类似。

2.6 C5卷积层

输入：S4层的全部16个单元特征map（与s4全相连）

卷积核大小：5*5

卷积核种类：120

神经元数量：120

输出特征映射大小：1*1（5-5+1）

可训练参数：120*（16*5*5+1）=48120

连接数：1*1*120*（16*5*5+1）=48120

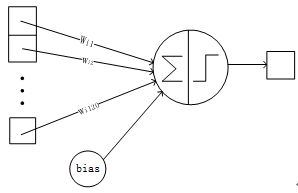
详细说明：C5层是一个卷积层。由于S4层的16个图的大小为5x5，与卷积核的大小相同，所以卷积后形成的图的大小为1x1。每个卷积核都与上一层的16个图进行卷积，形成120个卷积结果，所以共有(16*5*5+1)x120 = 48120个参数，同样有1*1*48120=48120个连接。C5层的网络结构如下：

2.7 F6全连接层

输入：c5 120维向量（120个卷积结果组成的向量）

计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。

神经元数量：84

可训练参数:84*(120+1)=10164

详细说明：6层是全连接层。F6层有84个节点，对应于一个7x12的比特图，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应于一个编码。该层的训练参数和连接数是(120 + 1)x84=10164。ASCII编码图如下：

 F6全连接层链接方式：

 2.8输出层

Output层也是全连接层

节点数：10，分别代表数字0到9

可训练参数：10*84=840

连接数：10*84=840

详细说明：如果节点i的值为0，则网络识别的结果是数字i。采用的是径向基函数（RBF）的网络连接方式。假设x是上一层的输入，y是RBF的输出，则RBF输出的计算方式之一（欧式距离）是：

上式w_ij 的值由i的比特图编码确定，i从0到9，j取值从0到7*12-1。RBF输出的值越接近于0，则越接近于i，即越接近于i的ASCII编码图，表示当前网络输入的识别结果是字符i。

3.总结

①LeNet-5是一种用于手写体字符识别的非常高效的卷积神经网络

②卷积神经网络能够很好的利用图像的结构信息

③卷积层的参数较少，这也是由卷积层的主要特性即局部连接和共享权重所决定

4.代码

各层的神经元个数进行了修改，且进行了模块化处理

import tensorflow as tf
import numpy as np
import pandas as pd
from tensorflow.examples.tutorials.mnist import input_data
import time
import matplotlib.pyplot as plt
import os
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "2"


def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def bias_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding="SAME")


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")


x = tf.placeholder("float32", [None, 784])
y_ = tf.placeholder("float32", [None, 10])

x_image = tf.reshape(x, [-1, 28, 28, 1])

W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
# h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_conv1 = myrelu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
# h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_conv2 = myrelu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

W_fc1 = weight_variable([7*7*64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
# h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
h_fc1 = myrelu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1, W_fc2) + b_fc2)

cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.GradientDescentOptimizer(1e-4).minimize(cross_entropy)

# 模型评价
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

c = []
index = []
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    mnist_data_set = input_data.read_data_sets("mnist", one_hot=True)
    start_time = time.time()

    # 迭代次数
    for i in range(500):
        batch_xs, batch_ys = mnist_data_set.train.next_batch(200)

        if i%2 == 0:
            train_accuracy = sess.run(accuracy, feed_dict={x: batch_xs, y_: batch_ys})
            print("step %d, training accuracy %g" % (i, train_accuracy))
            c.append(train_accuracy)
            index.append(i)
            cost_time = time.time()-start_time
            print("time:", cost_time)
            start_time = time.time()
        # 训练数据
        train_step.run(feed_dict={x: batch_xs, y_: batch_ys})

plt.figure(figsize=(10, 10))
plt.title("activation function - relu")
plt.rcParams["font.sans-serif"] = ["SimHei"]  # 设置显示字体
plt.rcParams["axes.unicode_minus"] = False  # 设置正常显示符号
plt.xlabel("迭代次数", size=12)
plt.ylabel("精确度", size=12)
plt.plot(index, c, color="g")
plt.show()