以逻辑回归预测癌症分类为引例介绍精确率、召回率、F1-score、ROC曲线与AUC指标
以逻辑回归预测癌症分类为引例介绍精确率、召回率、F1-score、ROC曲线与AUC指标
-
- 1、用逻辑回归对癌症分类预测
- 2、引入新的评估方法:精确率、召回率、ROC曲线和AUC指标
-
- 2.1 混淆矩阵,精确率,召回率,F1-score
- 2.2 ROC曲线与AUC指标
1、用逻辑回归对癌症分类预测
下面是用逻辑回归对癌症分类预测过程:
#1获取数据 读取的时候加上names #2数据处理 处理缺失值 #3数据集划分 #4特征工程 标准化 #5逻辑回归预估器 #6模型评估
import pandas as pd
import numpy as np
#1读取数据
column_name=['Sample code number','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape',
'Marginal Adhesion','Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli',
'Mitoses','Class']
data=pd.read_csv("breast-cancer-wisconsin.data",names=column_name)
data.head()
#class是标签 2代表良性 4代表恶性
#2处理缺失值
#将里面的问号替换成nan
data=data.replace(to_replace="?",value=np.nan)
#将里面的缺失样本删除
data.dropna(inplace=True)
data.isnull().any()#查看是否还有缺失值
#3划分数据集
from sklearn.model_selection import train_test_split
#先筛选特征值和目标值
x=data.iloc[:,1:-1]#data里面所有的行,第一列到倒数第二列
y=data["Class"]#data里面class那一列
x_train,x_test,y_train,y_test=train_test_split(x,y)#这样就划分好了数据集
#4数据集标准化
from sklearn.preprocessing import StandardScaler
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
#5模型训练
from sklearn.linear_model import LogisticRegression
estimator=LogisticRegression()
estimator.fit(x_train,y_train)
#逻辑回归的模型参数:回归系数和偏置
print("模型的回归系数:{}".format(estimator.coef_))
print("模型的回归偏置:{}".format(estimator.intercept_))
模型的回归系数:[[1.36376895 0.13112335 0.83907413 0.82860778 0.05631779 1.24576729
0.94812165 0.6708077 0.67124838]]
模型的回归偏置:[-0.93417385]
#6模型评估 这里采用准确率的方法
score=estimator.score(x_test,y_test)
print("采用逻辑回归预测的准确率是:{}".format(score))
采用逻辑回归预测的准确率是:0.9766081871345029
2、引入新的评估方法:精确率、召回率、ROC曲线和AUC指标
上述的逻辑回归对癌症分类的分数达到了97%,即100个样本中,有97个可以预测成功,看预测的准确率挺高,但是真的能够满足要求吗?这里可是预测一个人是否患有了癌症,这是一个很严肃的问题。如果有一个人获得了癌症,我们更关注的是预测的准不准,还是他真的得了癌症我们能不能检测出来?显然是后者。这个问题是很严肃的,显然分数90%多不行,比如上述的模型的分数97%,包不包括一个人真的患了癌症但是没有检查出来这种情况呢?显然是包括的,这种评估方法不行,所以要引入其他的评估方法,真的患癌症了能够被评估出来的概率。
2.1 混淆矩阵,精确率,召回率,F1-score
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)存在4中不同的组合,构成混淆矩阵(适用于多分类)

精确率:预测结果为正例样本中真实为正例的比例,如下图:

精确率,实际上是表明模型查的对不对;
召回率:真实为正例的样本中预测为正例的比例,如下图:

召回率,实际上是表明模型查的全不全。
还有其他的评估标准,F1-score,从下图中公式可以看出,F1-score越大表明精确率和召回率都很高,说明模型很稳健,用来衡量模型的稳健型。

回到刚才逻辑回归的例子,可以查看一下这个模型的精确率、召回率、F1-score,代码如下:
#查看精确率、召回率、F1-score
from sklearn.metrics import classification_report
print(classification_report(y_test,estimator.predict(x_test),labels=[2,4],target_names=["良性","恶性"]))
#2代表良性,4代表恶性

我们比较关心恶性的召回率,这里是96%,就是说假如100个人患有了恶性肿瘤,有96个人被我们查出来了,那还有4个人怎么办啊?这个问题就很严峻了,召回率应用场景最多的地方,这里是其中之一,还有一个应用的地方就是工厂里面质量检测,次品的召回率。
2.2 ROC曲线与AUC指标
假设有这么一种情况,总共有100个人,如果有99个样本癌症,1个样本非癌症,我们全部预测为正例(癌症),就是不管怎么样我都预测为正例(癌症),这实际上是一种很不负责任的模型,但是上述的准确率、精确率、召回率、F1-score这4个指标能不能反应出来这个模型不负责任呢?可以来算一算:
准确率:99%(有99个预测正确了);
精确率:99%(预测的100个癌症中实际上是有99个真的患癌症的);
召回率:99/99=100%(真实患癌症的有99个人,都被检测出来了);
F1-score:(2X精确率X召回率)/(精确率+召回率)=(2*99%*1)/(99%+1)=99.497%;
虽然我们的模型很不负责任(不管实际如何全部预测为患癌症,瞎猜),但是上述的4个指标都很高,没有反映出这个模型的不负责任性,这个时候引入新的指标:ROC曲线与AUC指标。
首先知道,什么是TPR与FPR。
TPR=TP/(TP+FN),所有真实类别为1的样本中预测类别为1的比例,就是前面的召回率;
FPR=FP/(FP+TN),所有真实类别为0的样本中,预测类别为1的比例。(这里再把混淆矩阵的图插入一遍,对照着看,方便一些)

ROC曲线:以FPR为横坐标,TPR为纵坐标,画出来的曲线如下图:
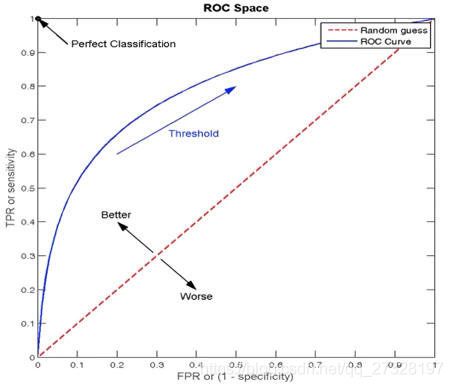
图中蓝色的曲线即为ROC曲线,ROC曲线与坐标轴包成的面积就是AUC指标,在上图中如果TPR=FPR,即不管样本真实为0还是1,都预测为了1,这个时候就是在瞎猜,就是如中的红色虚线random guess这种情况,此时与坐标轴包成的区域的面积AUC=0.5;
如果AUC=1,就是图中左上角Perfect Classification,此时TPR=1,FPR=0,真实样本为1的全部预测为1,真实样本为0的预测成1的没有,TPR>>FPR的极限位置,此时ROC曲线为左边的竖轴,此时与坐标轴围成的面积即AUC为1。
AUC的概率意义是随机取一对儿正负样本,正样本得分大于负样本得分的概率;AUC的最小值为0.5,最大值为1,取值越高越好;AUC=1,完美分类器;AUC=0.5,random guess,在瞎猜。
那么回到刚才讲的那个情况:总共有100个人,如果有99个样本癌症,1个样本非癌症,我们全部预测为正例(癌症)。准确率、精确率、召回率、F1-score这4个指标算出来都很高,没有把这个不负责任的模型给体现出来,那么AUC指标可以吗?AUC指标来计算一下:
TPR:99/99=1(99个人癌症都找出来了)
FPR:1/1=1(1个人没有患癌症,把这个1个人给预测成癌症了)
此时TPR=FPR,不就是ROC曲线中Random guess这种情况吗?AUC=0.5。因此,我们通过AUC指标这个把这个模型的不负责任性反应出来了。
那么本文的引例中的逻辑回归预测癌症分类的AUC指标是多少呢?可以通过以下代码查看:
#计算AUC指标
from sklearn.metrics import roc_auc_score
y_true=np.where(y_test>3,1,0)#将y_test中的2,4转换为0,1,因为计算AUC的API要求y_true是0(反例),1(正例)
print("AUC的值:{}".format(roc_auc_score(y_true,estimator.predict(x_test))))
AUC的值:0.9731974921630093
通过这个AUC指标,发现我们逻辑回归预测癌症分类的模型还是可以的!
补充:AUC只能用来评价而分类;AUC非常适合评价样本不平衡中的分类器的性能。

