L:python的Numpy模块:集合函数,多项式,数组组合和文件存取
集合函数
研究两个数组中的数据是否存在某种集合关系时,可使用集合函数。
x=np.arange(5) # array([0,1,2,3,4])
y=np.arange(3, 8) # array([3,4,5,6])
np.intersect1d(x, y) # 交集 , 注:不能使用集合的运算符号& | -
Out:array([3, 4]) # 1d 表示返回结果总是一维数组
np.union1d(x, y) # 并集
Out:array([0, 1, 2, 3, 4, 5, 6, 7])
np.setdiff1d(x, y) # 差集 x - y
Out: array([0, 1, 2])
np.setxor1d(x, y) # 对称差集, 不同时存在于x/y集合中
Out: array([0, 1, 2, 5, 6, 7])
多项式
np可构造多项式,可代入数值进行计算,还可求微分、积分、解方程。
y = np.poly1d([1, -3, -4]) # 以列表形式给出多项式系数,y是构造的多项式
Out: poly1d([ 1, -3, -4]) # y = x2 - 3x - 4
y([0.5, 1, 1.5]) # 分别计算x取0.5, 1, 1.5时多项式的值
Out: array([-5.25, -6. , -6.25])
np.roots(y) # 计算方程 的根
Out: array([ 4., -1.]) # 根为4和-1
p = np.poly1d([2, 4, 0, 3]) # 构造多项式p=2x3 + 4x2 + 3
z = p+y # p, y 两个多项式相加
Out: poly1d([ 2, 5, -3, -1]) # z = 2x3 + 5x2 - 3x - 1
z.deriv() # 微分
Out:poly1d([6, 10, -3]) # z' = 6x2 + 10x - 3
z.integ() # 积分
poly1d([ 0.5 , 1.66666667, -1.5 , -1. , 0. ])
多项式拟合:利用给定的自变量和因变量,按指定的最高次方拟合多项式。
x=[1, 2, 3] ; y=[ 2, 4.2, 5.8] 按一次式拟合 y = 1.9 x + 0.2
x = np.arange(1, 21) # 自变量
y1 = 3 * x + 2 + np.random.rand(20) # 构造测试数据y1并加入随机干扰值
coef = np.polyfit(x, y1, 1) # 按一次多项式拟合,拟合系数如下
Out: array([2.99028312, 2.5900484 ]) # y = 2.99x + 2.59
yn = np.poly1d(coef) # 拟合的多项式
yn(x) # 计算拟合值, 和 y1 对比一下,比较接近
y2 = x**2 + 3 * x + 1 + np.random.rand(20) # 构造测试数据y2
np.polyfit(x, y2, 2) # 按二次多项式拟合,拟合系数如下
Out: array([1.00000149, 3.01755285, 1.32390592]) # y = x2 + 3.02x +1.32
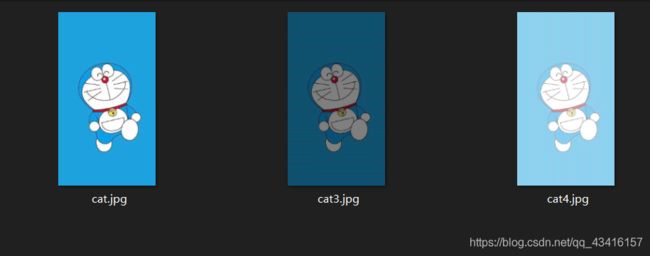
以猫图为例的数组应用
import numpy as np
from PIL import Image
a = np.array(Image.open('cat.jpg'))
# 高x宽x颜色,数据类型,某个点的颜色值
print(a.shape, a.dtype, a[0,0,:])
b = 255 - a # 互补色 RGB(255,0,0)
im = Image.fromarray(b.astype('uint8'))
im.save('cat2.jpg')
c = a.copy()
c[::2] = 0 #黑色横条
Image.fromarray(c).save('cat3.jpg')
c = a.copy()
c[:, ::2] = 255 #白色竖条
Image.fromarray(c).save('cat4.jpg')
#上下颠倒
Image.fromarray(a[::-1]).save('cat5.jpg')
#左右交换
Image.fromarray(a[:, ::-1]).save('cat6.jpg')
#水平组合
Image.fromarray(np.hstack((a,a))).save('cat7.jpg')
#垂直组合
Image.fromarray(np.vstack((a,a))).save('cat8.jpg')
#用tile平铺:纵/横轴都为2倍,颜色轴为1倍不变
Image.fromarray(np.tile(a, (2, 2, 1))).save('cat9.jpg')
#用repeat重复1轴 2次
Image.fromarray(np.repeat(a, 2, axis=1)).save('cat10.jpg')
数组组合和文件存取
改变数组维度:np提供了如下方法可改变数组的维度
1. reshape()方法
b=np.arange(12)
c=b.reshape(3, 4) # b不变,得到新的c,reshape()得到的是视图
d=c.reshape(-1, 6) # -1表示此轴的值由np自动计算得到
e=c.reshape(2, -1) # -1表示此轴的值由np自动计算得到
b.shape, c.shape, d.shape, e.shape
Out: ((12,), (3, 4), (2, 6), (2, 6))
2.设置shape属性或使用 resize() 方法
b.shape=(3, 4) # 直接改变b的形状
b.resize((3, 4)) # 直接改变b
3. 转置矩阵: 将行/列交换
d=c.transpose() # 或 c.T
4. 增加一个维度
ar = np.array([3,4,5]) # 原本是一维 ar.shape (3,)
ar2 = ar[:, np.newaxis] # 增加一个维度,变为二维。很多机器学习程序中处理数据集需要增加数据的维度。 ar2.shape (3, 1)
ar3 = ar2[:, :, np.newaxis] # ar3 三维
5. 将多维数组展平为一维数组
d1=b.ravel() # 将多维的b转为一维的d1, 视图
d2=b.flatten() #将多维的b转为一维的d2, 是复制,不是视图
数组元素的插入、删除
b=np.array([1, 3, 5, 7])
c=np.append(b, [9, 10]) # 插入, b不变,返回新数组c
Out:array([1, 3, 5, 7, 9, 10])
np.insert(b, 2, 20) # 在第2个位置插入20, b不变,返回新数组
Out:array([1, 3, 20, 5, 7])
np.delete(b, [0,1]) # 删除第[0,1]处数据,b不变,返回删除后的新数组
Out:array([5, 7])
数组组合
a = np.arange(6).reshape(2, 3)
b = np.arange(10, 16).reshape(2, 3)
1.水平组合 (复制)
np.hstack((a,b)) # 水平组合。行数不变,列数增加
np.concatenate((a,b), axis=1) # 效果同上
np.column_stack((a,b)) # 效果同上
2.垂直组合
np.vstack((a,b)) # 垂直组合。行数增加,列数不变
np.concatenate((a,b), axis=0) # 效果同上
np.row_stack((a,b)) # 效果同上
3.深度组合
c=np.dstack((a,b)) # 深度组合。a,b本是二维,c是三维
数组分割
1.水平分割 (视图)
b = np.arange(24).reshape(4, 6) # 生成4x6数组
x1, x2 = np.hsplit(b, 2) # 沿水平方向分为2个相同大小的4x3数组
x1, x2, x3 = np.hsplit(b, 3) # 沿水平方向分为3个相同大小的4x2数组
# x4含原数组第0列,x5含第1、2、3列,x6含的第4、5列
x4, x5, x6 = np.hsplit(b, [1, 4]) # 在第1, 4列分隔
b = np.arange(24).reshape(4, 6) # 4x6数组
y1, y2 = np.vsplit(b, 2) # 沿垂直方向分为2个相同大小的2x6数组
np.vsplit(b, 4) # 沿垂直方向分为4个相同大小的1x6数组
b = np.arange(24).reshape(2, 3, 4) # 2x3x4数组
v1, v2 = np.dsplit(b, 2) # 沿深度分为2个相同大小的2x3x2数组
v1.shape, v2.shape
Out: ((2, 3, 2), (2, 3, 2))
注:dsplit()只能用于维度>=3的数组,不能用于一、二维数组
读写文件
NumPy可以读写文本和二进制数据文件。
1.读写文本文件
b=np.arange(95, 101).reshape(2,3)
np.savetxt('data.txt', b) # 将数组b保存到data.txt 文件中,保存时默认按科学计数法格式
# 指定以逗号','分割, %i整数格式保存
np.savetxt('data2.txt', b, delimiter=',', fmt='%i')
!type data2.txt # 显示data2.txt文件内容
95,96,97
98,99,100
c=np.loadtxt('data2.txt', delimiter=',') # 读文本数据文件
2.读写.npy二进制格式文件
np.save('data', b) # 将数组b保存为data.npy文件,自动加扩展名.npy
d=np.load('data.npy') # 读取npy格式的二进制文件
b==d # 验证 b和d 是相等的
注:data.npy不能被pickle读取,因为二进制文件格式不同。
应用例子
节用NumPy给出一个骰子研究实例。有三颗骰子,每次一起抛出,现在用随机函数模拟抛掷1000次(1000x3)。
这1000次中有多少次投出“666”?有多少次出现三个骰子点数一样的情况?
如果假定最初有500个筹码,三个骰子的点数之和大于10算赢,小于等于10算输,
每次输赢一个筹码,那么最后是赢还是输?曾经达到的最大输赢数是多少?
import numpy as np
np.random.seed(7) # 注释该行则每次测试有变化
num = 1000 # 抛掷总次数
# 产生1000x3数组dice,随机整数范围[1,6],注意函数中要写为7
dice = np.random.randint(1, 7, size=(num, 3))
# 为编程方便,计算三个骰子的点数之和,添加到dice末尾列,现在是1000x4数组
dice = np.column_stack((dice, dice.sum(axis=1)))
point = dice[:, 3] # 取点数之和列(第3列)
print('投掷出666的次数:', (point == 18).sum()) # 出现666的次数
print('666出现在第x次', np.where(point == 18)) # 出现在第x次
# 找出三次投掷点数一样的行,得到一个布尔数组,注意 np.logical_and 函数
condition = np.logical_and(dice[:, 0] == dice[:, 1], dice[:, 1] == dice[:, 2])
print('\n三次投掷点数均相同的次数:', condition.sum()) # 计算True的次数
print('投掷情况为:', dice[condition]) # 显示True对应的行
money = 500 # 初始筹码数
bep = 10 # >10赢,<=10输
print('\n初始筹码:', money, ', 盈亏点:', bep, ', 每次输赢1')
# 只需简单统计> bep和<= bep的次数之和,即可计算最后的筹码数
total = money + (point > bep).sum() - (point <= bep).sum()
print('最后筹码:', total)
# 计算投掷过程中曾经达到的最高筹码数、最低筹码数
# np.where判断每次输赢,返回1,-1构成的每次盈亏列,添加到末尾列,变为1000x5
dice = np.column_stack((dice, np.where(dice[:, 3] > bep, 1, -1)))
# np.cumsum累加每次盈亏列,得到累积盈亏列,添加到末尾列,变为1000x6
dice = np.column_stack((dice, np.cumsum(dice[:, 4])))
# 累积盈亏列加初始筹码数,得到当前筹码列,添加到末尾列,变为1000x7
dice = np.column_stack((dice, dice[:, 5] + money))
s = '曾经的最高筹码数{}, 出现在第{}次'
print(s.format(np.max(dice[:, 6]), np.argmax(dice[:, 6])))
s = '曾经的最低筹码数{}, 出现在第{}次'
print(s.format(np.min(dice[:, 6]), np.argmin(dice[:, 6])))
np.set_printoptions(threshold=10000) # 输出数据个数的门槛
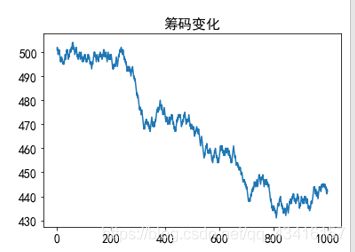
#筹码变化图
import matplotlib.pyplot as plt # 引入绘图库
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定中文黑体字体
plt.xticks(fontsize=14) # 设x轴文字大小
plt.yticks(fontsize=14) # 设y轴文字大小
plt.title('筹码变化', fontsize=16) # 设标题文字
plt.plot(dice[:, -1]) # 画筹码变化折线图
投掷出666的次数: 2
666出现在第x次 (array([ 99, 865], dtype=int64),)
三次投掷点数均相同的次数: 22
投掷情况为: [[ 5 5 5 15] … …
初始筹码: 500 , 盈亏点: 10 , 每次输赢1
最后筹码: 442
曾经的最高筹码数504,出现在第57次
曾经的最低筹码数431, 出现在第810次