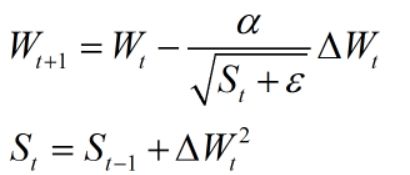bp神经网络及改进（python）
bp神经网络及改进（python）
- 批量梯度下降法（Batch Gradient Descent，BGD）
- 随机梯度下降法（Stochastic Gradient Descent，SGD）
- 小批量梯度下降法（Mini-batch Gradient Descent，Mini-batchGD）
- 对SGD用动量算法（Momentum）
- 对SGD用Nesterov加速梯度下降法
- 对SGD用自适应学习率（Adagrad）
- 对SGD用均方根自适应学习率（RMSprop）
- 自适应增量（Adadelta）
参考：
BP神经网络代码
10个梯度下降优化算法
神经网络泰坦尼克号
深度学习面试题04
批量梯度下降法（Batch Gradient Descent，BGD）
计算代价函数梯度的时候考虑全部样本，即全部样本训练完后再更新权值。
例如，共有k个样本，每个样本输入n1维，输出n2维，假设只有一层隐藏层，隐藏层神经元个数为m个。
一般传统方法：
取一个样本，先前向传播计算
再反向传播，更新权值
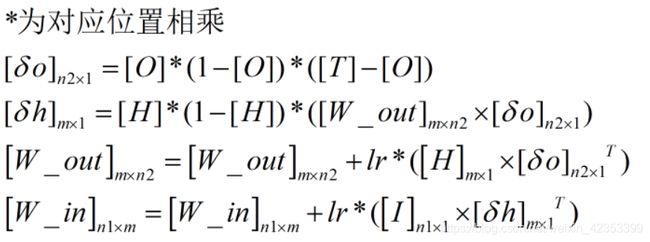
然后再计算下一个样本再更新。
而批量梯度下降法是先计算出所有的样本的前向传播，只进行一次权值更新。
k个样本一齐输入，计算输出。取均值更新权值
1、建立网络
def setup_BGD(self, ni, nh, no,input_w,output_w,length):
self.input_n = ni
self.hidden_n = nh
self.output_n = no
self.input_cells = np.ones([self.input_n,length])
self.hidden_cells = np.ones([self.hidden_n,length])
self.output_cells = np.ones([self.output_n,length])
self.input_weights = np.zeros([self.input_n, self.hidden_n])
self.output_weights = np.zeros([self.hidden_n, self.output_n])
# 初始权值由外部传入
k=0
for i in range(self.input_n):
for h in range(self.hidden_n):
self.input_weights[i][h] = input_w[k]
k=k+1
k=0
for h in range(self.hidden_n):
for o in range(self.output_n):
self.output_weights[h][o] = output_w[k]
k=k+1
2、前向传播
def predict_BGD(self, inputs):
# activate input layer
self.input_cells[:-1,:] = inputs
# activate hidden layer
self.hidden_cells=sigmoid(np.dot(self.input_weights.T,self.input_cells))
# activate output layer
self.output_cells=sigmoid(np.dot(self.output_weights.T,self.hidden_cells))
return self.output_cells
3、反向传播
def back_propagate_BGD(self, case, label, learn, correct,length):
# feed forward
self.predict_BGD(case)
# get output layer error
error=label-self.output_cells
output_deltas=sigmoid_derivative(self.output_cells) * error
# get hidden layer error
error=np.dot(self.output_weights,output_deltas)
hidden_deltas=sigmoid_derivative(self.hidden_cells) * error
# update output weights
change = np.dot(self.hidden_cells,output_deltas.T)/length
self.output_weights += learn * change
# update input weights
change = np.dot(self.input_cells,hidden_deltas.T)/length
self.input_weights += learn * change
error=0.5*sum(sum(label-self.output_cells)**2)
return error
取学习步长lr=0.5，训练2000回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差： 399.94341939856747 测试误差： 75.00346008629134
平均用时： 4.30466138
随机梯度下降法（Stochastic Gradient Descent，SGD）
就是前面说的一般传统方法，每来一个样本更新一次权值。
def predict_SDG(self, inputs):
self.input_cells[:-1] = np.array([inputs]).T
self.hidden_cells=sigmoid(np.dot(self.input_weights.T,self.input_cells))
self.output_cells=sigmoid(np.dot(self.output_weights.T,self.hidden_cells))
return self.output_cells
def back_propagate_SDG(self, case, label, learn, correct):
self.predict(case)
error=label.T-self.output_cells
output_deltas=sigmoid_derivative(self.output_cells) * error
error=np.dot(self.output_weights,output_deltas)
hidden_deltas=sigmoid_derivative(self.hidden_cells) * error
# update weights
change = np.dot(self.hidden_cells,output_deltas.T)
self.output_weights += learn * change
change = np.dot(self.input_cells,hidden_deltas.T)
self.input_weights += learn * change
# get global error
error=0.5*sum(label.T-self.output_cells)**2
return error
def train_SDG(self, cases, labels, epoch=2,learn=0.05, correct=0.1):
a=len(cases)
data=np.hstack((np.array(cases),np.array(labels)))#水平合并
for j in range(epoch):
cases=data[:,:-1]
labels=data[:,-1]
error = 0.0
for i in range(a):
error += self.back_propagate(cases[i], labels[i], learn, correct)
return error
取学习步长lr=0.5，循环训练3回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差： [274.17459107] 测试误差： [62.79596978]
平均用时： 1.1661673099999974
小批量梯度下降法（Mini-batch Gradient Descent，Mini-batchGD）
每次取一小部分数据来计算前向传播，更新权值，介于BGD和SGD方法之间。
def train_MBGD(self, cases, labels, epoch=20, learn=0.05, correct=0.1,batch=128):
b=len(cases)
a=int(np.ceil(b/batch))
cases=np.array(cases).T
labels=np.array(labels).T
for j in range(epoch):
error = 0.0
for i in range(a):
if i<a-1:
error += self.back_propagate_BGD(cases[:,i*batch:(i+1)*batch], labels[:,i*batch:(i+1)*batch], learn, correct,batch)
else:
x=np.random.randint(0,b-batch)
cases1=np.hstack((cases[:,i*batch:],cases[:,x:(i+1)*batch-b+x]))#水平合并
labels1=np.hstack((labels[:,i*batch:],labels[:,x:(i+1)*batch-b+x]))#水平合并
error += self.back_propagate_BGD(cases1, labels1, learn, correct,batch)
return error
取学习步长lr=0.5，训练重复回数epoch为250，批大小128，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差： 333.7609109395646 测试误差： 66.46165953378532
平均用时： 1.0842400800001997
对SGD用动量算法（Momentum）
在更新时做改变
# update output weights
change = np.dot(self.hidden_cells,output_deltas.T)
vt=(1-correct)*change + correct * self.output_correction#用动量算法
self.output_weights += learn * vt
self.output_correction = vt
# update input weights
change = np.dot(self.input_cells,hidden_deltas.T)
vt=(1-correct)*change + correct * self.input_correction#用动量算法
self.input_weights += learn * vt
self.input_correction = vt
取学习步长α=0.5，β=0.9，循环训练3回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差 [310.75273205]， 测试误差 [60.93167491]
平均用时： 1.2287481600000008
对SGD用Nesterov加速梯度下降法
与动量算法不同的地方：
V t = β V t − 1 + ( 1 − β ) Δ W ∗ V_t = {\beta}V_{t-1}+(1-\beta) {\Delta}W^* Vt=βVt−1+(1−β)ΔW∗
W ∗ = W t + α V t − 1 W^* = W_{t}+{\alpha} V_{t-1} W∗=Wt+αVt−1
# update output weights
change = np.dot(self.hidden_cells,output_deltas.T)
vt=(1-correct)*change + correct * self.output_correction#用NAG
self.output_weights += learn * vt
self.output_correction = vt
self.output_weights+=learn * vt
# update input weights
change = np.dot(self.input_cells,hidden_deltas.T)
vt=(1-correct)*change + correct * self.input_correction#用NAG
self.input_weights += learn * vt
self.input_correction = vt
self.input_weights += learn * vt
取学习步长α=0.5，β=0.9，循环训练3回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差 [292.50970942]， 测试误差 [57.79989716]
平均用时： 1.4032514599999786
对SGD用自适应学习率（Adagrad）
# update output weights
change = np.dot(self.hidden_cells,output_deltas.T)
st=self.output_correction+change**2#自适应学习率
self.output_weights += learn * change / (st+10**-7)**0.5
self.output_correction=st
# update input weights
change = np.dot(self.input_cells,hidden_deltas.T)
st=self.input_correction+change**2#自适应学习率
self.input_weights += learn * change / (st+10**-7)**0.5
self.input_correction=st
取学习步长α=0.5，循环训练3回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差 [302.91083596]， 测试误差 [47.64498746]
平均用时： 1.3652030899998864
对SGD用均方根自适应学习率（RMSprop）
相比自适应，St表达式为：
取学习步长α=0.05，循环训练3回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差 [308.03087979]， 测试误差 [46.49391691]
平均用时： 1.5230551099998593
自适应增量（Adadelta）
（前面的 Δ W t {\Delta}W_t ΔWt都是 ∂ L ∂ W t \frac{ {\partial L}}{ {\partial W_t}} ∂Wt∂L ）
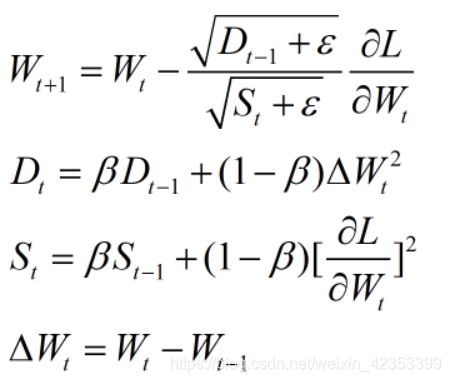
change = np.dot(self.hidden_cells,output_deltas.T)
st=correct*self.output_correction+(1-correct)*change**2
self.output_weights1=self.output_weights#W_t-1
self.output_weights += (self.output_correction1+10**-7)**0.5 / (st+10**-7)**0.5 * change
dt=correct*self.output_correction1+(1-correct)*(self.output_weights-self.output_weights1)**2
self.output_correction1=dt
self.output_correction=st
# update input weights
change = np.dot(self.input_cells,hidden_deltas.T)
st=correct*self.input_correction+(1-correct)*change**2
self.input_weights1=self.input_weights#W_t-1
self.input_weights += (self.input_correction1+10**-7)**0.5 / (st+10**-7)**0.5 * change
dt=correct*self.input_correction1+(1-correct)*(self.input_weights-self.input_weights1)**2
self.input_correction1=dt
self.input_correction=st
取β=0.9，循环训练2回，数据输入8维，输出1维，训练集共有10776条，测试集有1739条。运行10次，得到结果及平均运行时间：
训练误差 [386.34831587]， 测试误差 [72.40686732]
平均用时： 1.2307410600000366