路径跟踪—基于车辆运动学方程的离散时间LQR控制仿真

---

前言

路径跟踪，轨迹跟踪的算法有基于运动学和基于动力学的，其中LQR算法基于车辆动力学网上有很多，毕竟百度开源了apollo，该算法通过简单改进后的实车效果还是非常棒的，之前通过dSPACE MicroAutoBox做了试验，横向误差都是厘米级。由于动力学模型需要估计车辆重量，轮胎侧偏刚度，还有绕Z轴转动惯量，需要估计的参数非常多，相对而言，运动学则简单了很多，不需要估计很多参数，且听某FSAC车队的大佬说，运动学模型非常稳定，于是我动手用Simulink搭了一下，跟各位分享一下建模过程，因为在网上找的基本都是MPC，感觉不用MPC都不好意思出门了，就是找不到基于运动学的LQR算法，所以动手实践下，搭起来也非常简单，并且年后找个机会实车测试一下。

一、运动学模型

运动学模型很多博客都提到过，这里分享个视频，如果不清楚运动学模型推导的可以仔细跟着做一遍。
【控制】模型预测控制 MPC 【合集】Model Predictive Control
这里，我就通过图片的方式直接呈现运动学模型，该运动学模型需要线性化和离散化，因为实际系统都是离散的，所以根据需要的采样时间进行离散化即可。

其中，Vr是车辆后轴速度，φ是车辆横摆角，δf是车辆前轮转角，l是轴距。
然后把上面方程线性化，离散化后，直接得出如下方程：

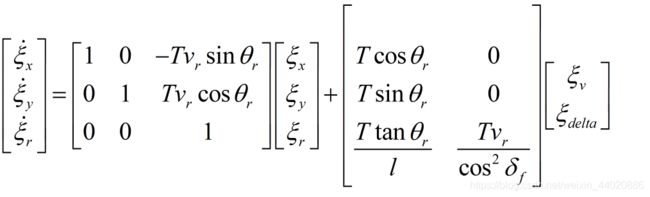
将模型变为了偏差的方程，分别是状态变量和控制变量都是偏差值：实际值减去期望的偏差值。那么可以发现，系统矩阵和控制矩阵都是时变的，因此必须在每个控制时刻都进行黎卡提方程的求解得到控制量，注意，此刻的控制量是变化量，必须加上期望值，才是最后的控制量，输入给车辆。这里和动力学模型是大不同的。
期望速度很好理解，提前给定就行。前轮转角则是通过车辆轴距和当前车辆与路径最近点的曲率值乘积的反正切值。有了上述模型，则可以进行建模与仿真。

二、建模仿真

这里给各位分享一下，我是如何搭建这个模型的，并且给出整个控制算法的代码，该代码是可以进行Code Generation的。下面就是仿真模型，该模型分为三部分。第一部分为控制算法，第二部分为车辆模型，第三部分是可视化界面，这部分可有可无。Matlab版本：R2019b。

先看一下车辆模型，为了方便用的车辆动力学工具箱的3dof 车辆模型搭建。

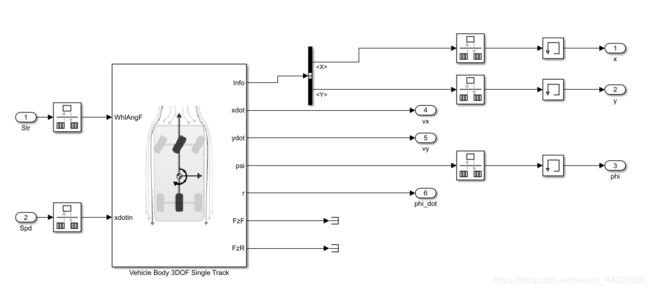
模型输入：前轮转角(rad); 车辆纵向速度(m/s)
模型输出：车辆后轴位置横坐标x(m);车辆后轴位置横坐标 y(m);车辆横摆角(rad)。
其余输出为可视化界面使用，有纵向速度vx,侧向速度vy，以及横摆角速度φdot。
rate trasition模块是因为整个模型使用变步长求解，因为定步长求解这个车辆模型很慢。但是控制算法是原子子系统，10ms运行一次。因为运动学离散时间为10ms。memory模块是为了避免代数环。
控制算法部分如图所示，控制算法通过m函数编写,将该子系统设置为原子子系统采样时间10ms。

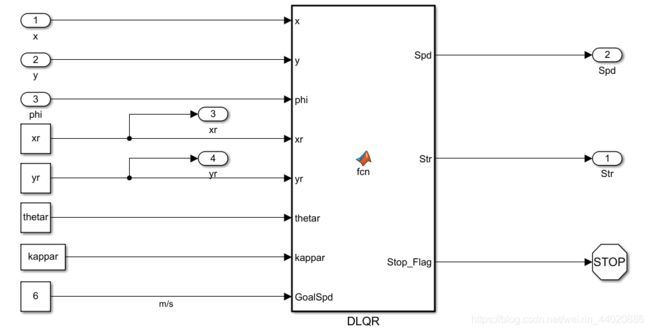
该控制算法的输入有车辆当前后轴横坐标x，纵坐标y以及横摆角φ。车辆期望的路径通过离散点的形式存入Basic/Model workspace并通过Constant模块给出，包括路径的横纵坐标，每个坐标的航向角以及每个坐标的曲率。车辆期望速度通过Constant模块给出。
模型输出控制车速以及前轮转角(rad)。该车速是期望车速，按理说应该通过纵向控制输出加速度，后反算成转矩给车辆发动机或者电机。这里省略纵向控制直接将车速给到车辆模型。
下面直接给出M函数的代码。如果对代码有疑问的同学，可以私聊我进行讨论。

function [Spd,Str,Stop_Flag]  = fcn(x,y,phi,xr,yr,thetar,kappar,GoalSpd)
%****初始化参数矩阵************%
global index;
T = 0.01;%程序离散控制周期，配合原子子系统0.01ms周期
L = 1.6;%车辆轴距
PN_1 = zeros(3,3); %该矩阵用于黎卡提方程迭代
n=length(xr);      %路径点个数
Stop_Flag = 0;     %仿真结束标志位
I = eye(3);        %初始化3*3单位矩阵
K =zeros(2,3);     %初始化反馈增益矩阵维度
%coder.extrinsic('dlqr'); %若用自带库函数，请用外部声明
min=1;
%*******寻找车辆后轴与当前车辆最近点，仅查找距上一次车辆位置最近点前30个点
    if index == 0  %%未开始
		d_min=(x-xr(1))^2+(y-yr(1))^2;
		min=1;
		for i=1:30 %% search 1-30 points when car is running.
			d=(x-xr(i))^2+(y-yr(i))^2;
			if d<d_min
				d_min=d;
				min=i;
			end
		end
		dmin=min;
		index = dmin; %% 当前点索引分配给index;
    else
		d_min = (x-xr(index))^2+(y-yr(index))^2;
		min = index;
		if index <= n - 30
			for i = index:index+30
				d=(x-xr(i))^2+(y-yr(i))^2;
				if d<d_min
					d_min=d;
					min=i;
				end
			end
			dmin=min;
			index = dmin;
		else 
			for i = index:n
				d=(x-xr(i))^2+(y-yr(i))^2;
				if d<d_min
					d_min=d;
					min=i;
                    if min == n
                        Stop_Flag =1;%路径点跑完了仿真停止
                    end
				end
			end
			dmin=min;
			index = dmin; 
		end
    end
%*****状态变量计算******%
kesix = x -xr(dmin);
kesiy = y -yr(dmin);
kesir =phi - thetar(dmin);
  %******防止偏差数据溢出***********%
    if kesir < -3.14
        kesir = kesir+6.28;
    end
    if kesir >3.14
        kesir = kesir -6.28;
    end

xstate = [kesix;
          kesiy;
          kesir];%状态变量
vd1 = GoalSpd; %期望速度
t_d = thetar(dmin);%当前和车辆最近点的航向角
k = kappar(dmin);%当前和车辆最近点的曲率
vd2=atan(L*k);%期望前轮转角

Ad=[1    0   -vd1*sin(t_d)*T;
    0    1   vd1*cos(t_d)*T;
    0    0    1;];  %线性离散后的系统矩阵
   
Bd=[cos(t_d)*T     0;
    sin(t_d)*T     0;
    tan(vd2)*T/L   vd1*T/(L*(cos(vd2)^2))]; %线性离散后的控制矩阵
   
 Q = [10 0 0;
      0 10 0; 
      0 0 10];%初始化LQR的权重矩阵
 R =[5 0;
     0 5];%初始化LQR的权重矩阵
 
 %*********黎卡提方程求解**********%
 PN =Q;  
 err =10^(-1);%该精度根据需要调整，误差越小迭代次数越多
 error = 1;
 while(error>err)
        PN_1 = Q+Ad'*PN/(I+Bd/R*Bd'*PN)*Ad;%黎卡提方程
        error = norm(PN-PN_1);
        PN =PN_1;
        i = i+1;%观察迭代步数
        if i>40000 %防止迭代次数过长，该值根据控制器实际性能设置
            break;
        end
 end
 P =PN_1;
 K = (R+Bd'*P*Bd)\Bd'*P*Ad;%计算状态反馈增益K
  %***************************************%
  
%K =dlqr(Ad,Bd,Q,R); %使用官方求解库，配合外部函数引用才有效，否则报错。
 U  = - K * xstate; %线性反馈控制量
 deltav = U(1);
 deltastr =U(2);
 
 Spd = GoalSpd+deltav; %m/s
 Str = vd2+deltastr; %rad
end

若您在模型中已经做了规划层的算法，可以直接将唯一的规划点传入控制算法，就省去了搜索路径点最近点的一系列程序。程序反而更加简洁。上述程序直接将所有路径点以行向量的形式传入了函数中。
注意index是全局变量，需要在Edit Data中声明该变量是data store memory。然后在Simulink中添加data store memory模块，并填写数据类型。
接下来可以进行仿真，如果没有可视化界面的同学或者不会用的同学就将xy输出到matlab界面画图对比期望路径。

从动画界面可以看出车辆完全可以跟踪期望路径，这里感谢一下北理工车队提供FSAC2020赛季的高速循迹赛道数据库。该算法的全部过程如上，希望各位有兴趣的朋友可以动手搭一下，最核心的控制算法已经全部给出，可以联合Carsim进行仿真。也可以直接进行Code Gen部署到ROS或者直接刷写进Speedgoat或者AutoBox，前提是不能使用自带dlqr函数，因自带lqr函数无法代码生成。这里简单生成下C代码：

总结

动力学模型的LQR就不介绍了，网上有很多，并且后续会进行运动学和动力学模型的实车试验进行对比，结合控制器性能和算法稳定性综合评价选出最合适的算法。如果您对本次算法有任何不解，欢迎私信讨论。感兴趣的同学建议您自己动手实践一下，最核心的代码已经完全给出，实现起来还是非常简单的，有问题，请直接打扰。

更新

如果仅想获取模型的朋友，可以通过下面链接下载，原创不易，谢谢支持。Matlab版本请更新到2019b及以上，并安装控制系统工具箱以及车辆动力学工具箱。
Matlab/Simulink基于运动学的LQR轨迹跟踪控制算法