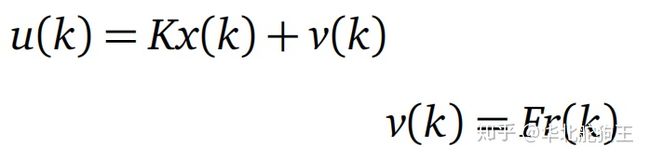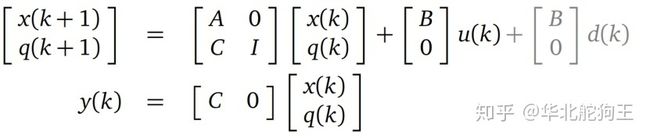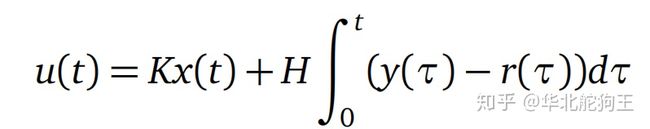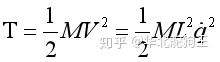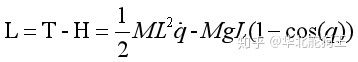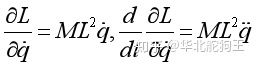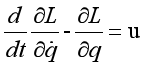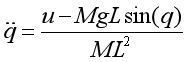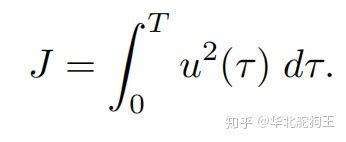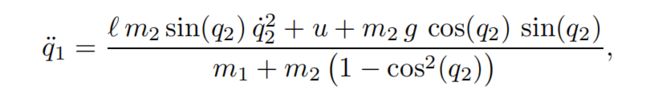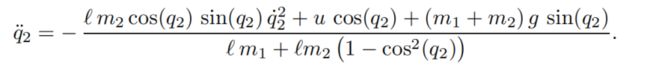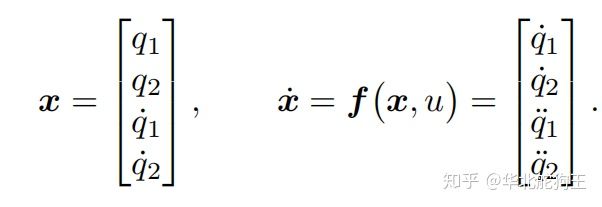连不上机器判断机器状态_四足机器人优化方法: 状态反馈与轨迹优化1
1. 状态反馈+参考状态跟踪
在控制方法中反馈系统的控制占了绝大一部分，而且很多资料介绍中主要是这一块的系统设计，在现代控制理论方法指导下构建一个基于模型的闭环系统有很成熟的方法，但在很多实际系统中主要还是以PID的测量误差反馈控制作为代替，以典型的线性控制系统设计为例，在获取到系统的状态空间方程后就可以基于极点配置或者LQR等方法来设计控制器，值得注意的是这一类状态反馈主要目的是保证系统状态收敛到稳定状态，以倒立摆为例我们往往会在其期望的竖直稳定点附近进行线性化，因此最终的状态反馈控制结果也是让其保证竖直状态，而如果需要让小车能随期望轨迹移动，则为解决状态跟踪Reference tracking问题，即然系统输出跟踪期望设定，因此需要在传统的状态镇定输出上再加上一部分状态转移所需要的控制量：
其中状态转移的期望增益矩阵为：
上述系统中首先采用LQR最优控制方法保证系统的镇定求取对应的控制增益矩阵K，而矩阵F可以基于系统模型和控制矩阵进行求解，当在实际系统中由于误差的存在，如系统存在摩擦等因素带来的外部扰动，会导致最终系统输出与期望存在固定或者时变的误差，即构成如下的系统模型：
为解决外扰动带来的控制静差，可以通过增加积分环节进行消除，以状态扩维的方式将扰动作为系统状态的扩张，并得到一个新的状态空间方程：
进一步基于LQR方法求取对应的状态反馈增益来，另外也可以直接引入测量误差反馈构建积分环节，构成如下的系统模型：
下面给出一个参考网上开源例子的Cart Pole小车倒立摆的LQR仿真例子：
clc;
clear all;
%模型参数
J1=2e-3;%旋转臂转动惯量
m=0.127;%摆杆质量
L=0.337;%摆杆长度
R=0.2159;%悬臂长度
km=7.68e-3;%反电动系数
kt=7.68e-3;%电机力矩系数
Rm=2.6;%电驱电阻
Be=2.4e-3;%摩擦阻尼
J2=4.3e-3;%摆杆转动惯量
Vm=0;%电机电压
l=0.156;%摆杆质心长度
r=0.0618;%悬臂质心长度
kg=5;%减速比
nm=0.69;%电机效率
ng=0.9;%变速器效率
g=9.8;
E=J1*J2+J1*m*l*l+J2*m*R*R;
b=nm*ng*kt*kg/Rm;
k1=m*l*l*g*R/E;
k2=(Be+b*km*kg)*(J2+m*l*l)/-E;
k3=m*l*R*Be/-E;
k4=m*l*g*(J1+m*R*R)/E;
k5=(Be+b*km*kg)*m*l*R/-E;
k6=(J1+m*r*r)*Be/-E;
k7=b*(J2+m*l*l)/E;
k8=b*m*l*R/E;
% 悬臂 摇臂
%ss= sita alfa dsita dalfa
A=[0 0 1 0;
0 0 0 1;
0 k1 k2 k3;
0 k4 k5 k6];
B=[0;0;k7;k8];
C=[1 0 0 0;0 1 0 0];
D=[0;0];
states = { 'sita' 'alfa' 'dsita' 'dalfa'};
inputs = {'u'}; outputs = { 'sita' 'alfa'};
sys_ss = ss(A,B,C,D,'statename',states,'inputname',inputs,'outputname',outputs)
x0=[180/57.3, 5/57.3, 0 ,0]
%x0=[0, 180/57.3, 0 ,0]
Q = C'*C;
Q(1,1) = 10;%pos权重
Q(2,2) = 15;%
Q(3,3) = 50;%角度权重 sita
Q(4,4) = 100;% alfa
R = 1;
K = lqr(A,B,Q,R)
Ac = (A-B*K);
Bc = B;
Cc = C;
Dc = D;
states = {'x' 'x_dot' 'phi' 'phi_dot'};
inputs = {'r'};
outputs = {'x'; 'phi'};
sys_cl = ss(Ac,Bc,Cc,Dc,'statename',states,'inputname',inputs,'outputname',outputs);
t = 0:0.01:10;
r =0.2*ones(size(t));
Cn = [1 0 0 0];%输入补偿器 只针对位置 只针对单输入
sys_ss = ss(A,B,Cn,0);
Nbar = rscale(sys_ss,K)
% [y,t,x]=lsim(sys_cl,r,t);
% [AX,H1,H2] = plotyy(t,y(:,1),t,y(:,2),'plot');
% set(get(AX(1),'Ylabel'),'String','cart position (m)')
% set(get(AX(2),'Ylabel'),'String','pendulum angle (radians)')
% title('Step Response with LQR Control')
function[Nbar]=rscale(a,b,c,d,k)
% Given the single-input linear system:
% .
% x = Ax + Bu
% y = Cx + Du
% and the feedback matrix K,
%
% the function rscale(sys,K) or rscale(A,B,C,D,K)
% finds the scale factor N which will
% eliminate the steady-state error to a step reference
% for a continuous-time, single-input system
% with full-state feedback using the schematic below:
%
% /---------
% R + u | . |
% ---> N --->() ---->| X=Ax+Bu |--> y=Cx ---> y
% -| ---------/
% | |
% |<---- K <----|
%
%8/21/96 Yanjie Sun of the University of Michigan
% under the supervision of Prof. D. Tilbury
%6/12/98 John Yook, Dawn Tilbury revised
error(nargchk(2,5,nargin));
% --- Determine which syntax is being used ---
nargin1 = nargin;
if (nargin1==2), % System form
[A,B,C,D] = ssdata(a);
K=b;
elseif (nargin1==5), % A,B,C,D matrices
A=a; B=b; C=c; D=d; K=k;
else error('Input must be of the form (sys,K) or (A,B,C,D,K)')
end;
% compute Nbar
s = size(A,1);
Z = [zeros([1,s]) 1];
N = inv([A,B;C,D])*Z';
Nx = N(1:s);
Nu = N(1+s);
Nbar=Nu + K*Nx;
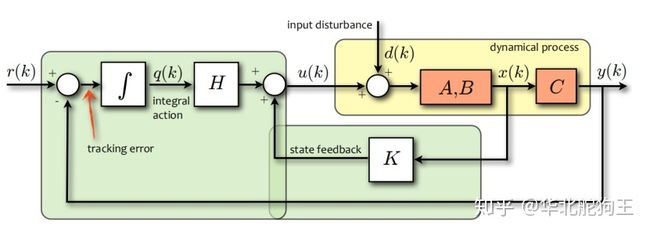
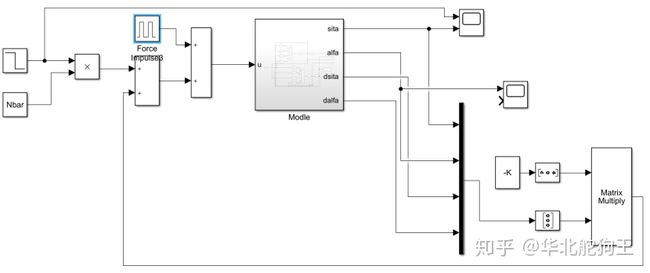
end系统模型框图如下：
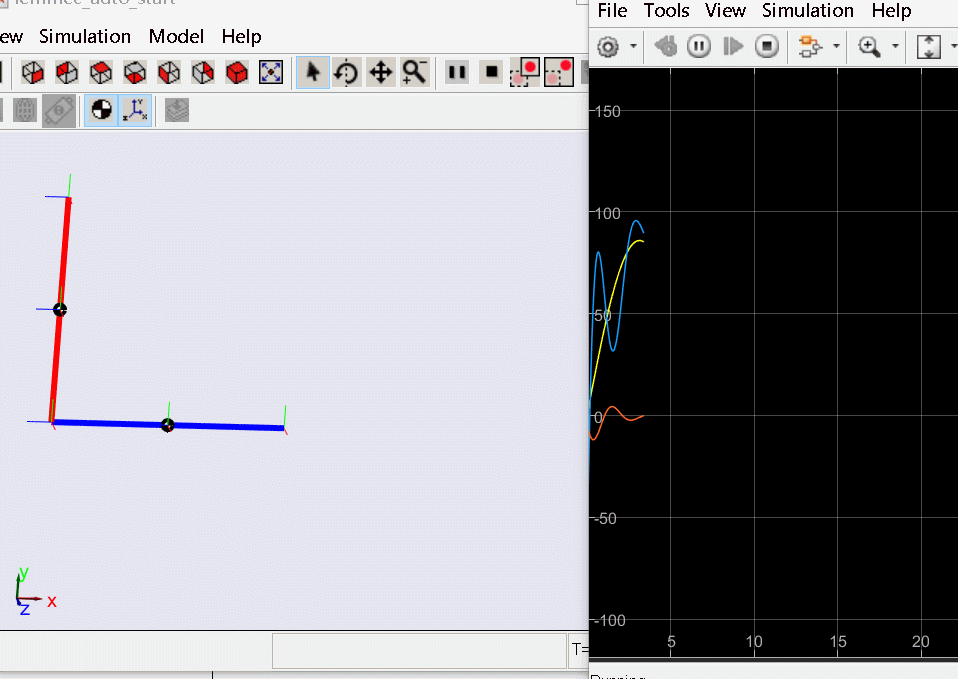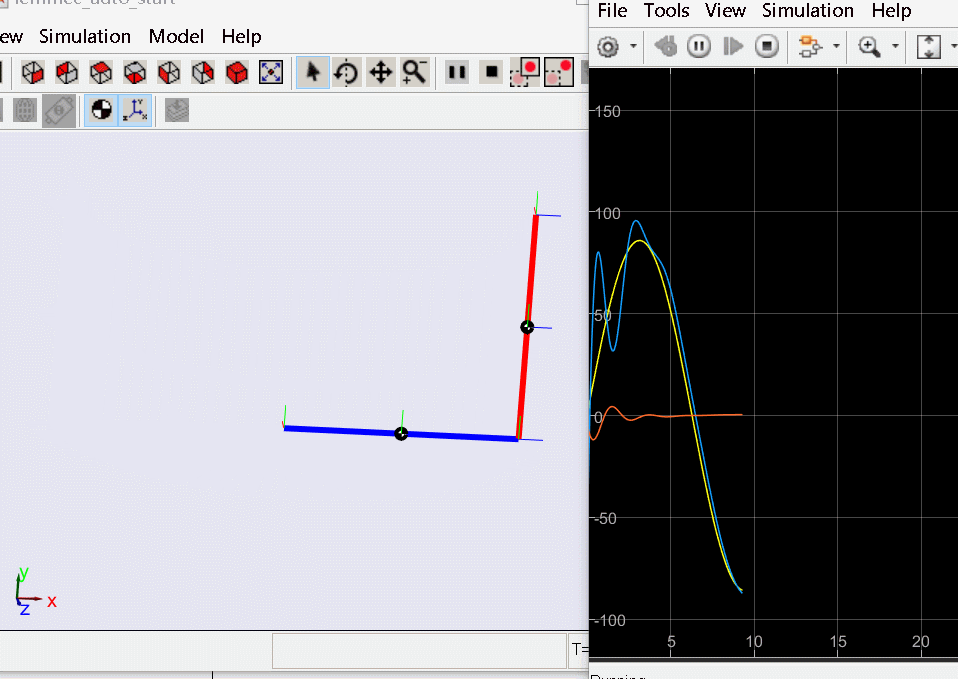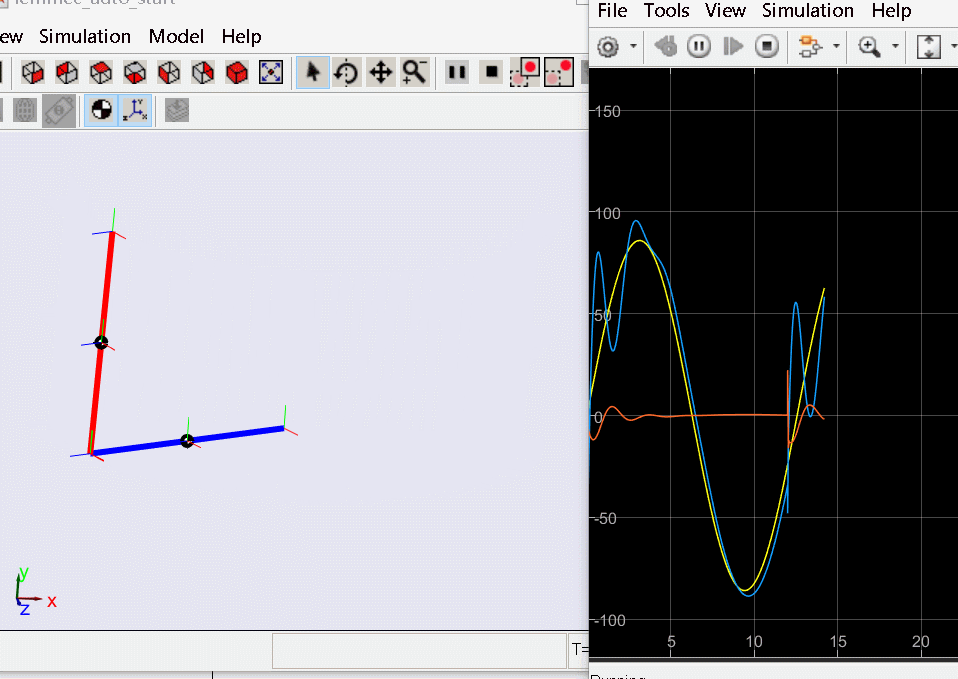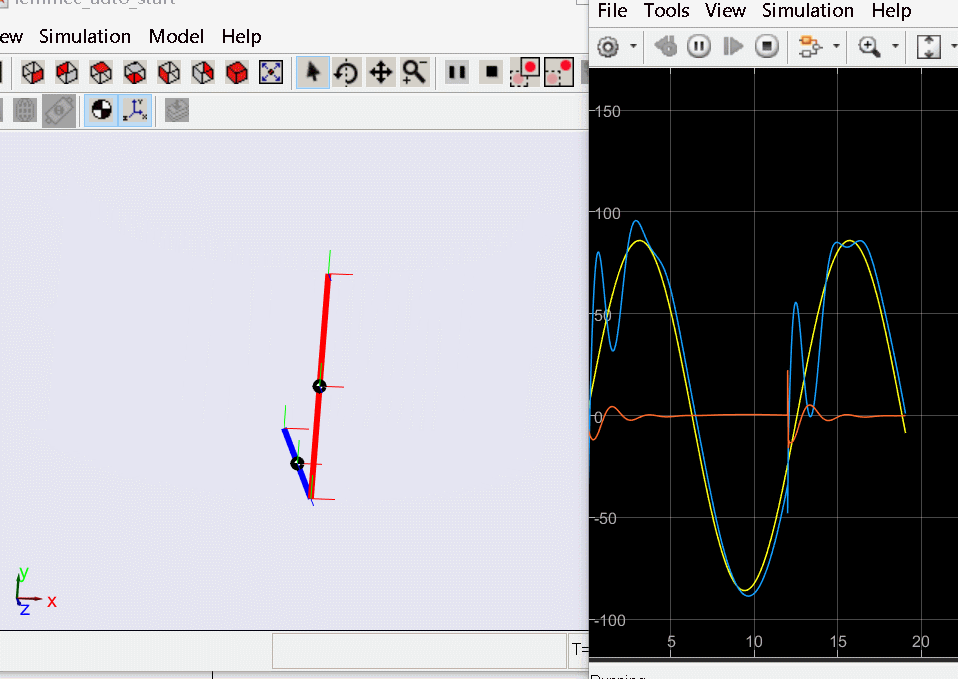
基于上述状态反馈控制器能很好地完成对倒立摆系统的稳定和期望状态轨迹的跟踪，因此我们可以将其推广到更复杂的控制模型中，下面给出一阶旋转倒立摆的仿真：
下面的代码基于网上开源例子，如需要我修改的代码可通过知乎咨询功能获取！！
上述反馈控制方法只能保证倒立摆在竖直状态，如要实现从锤下开始启摆过程则很难直接基于反馈控制的方式实现，解决启摆通用的方法是轨迹规划来获取从初始状态致期望竖直状态的连续轨迹，该轨迹除了受模型约束外还可以增加最小时间、最小控制输入等多个约束，而在完成轨迹规划后既可以使用各阶状态构建反馈和前馈控制实现倒立摆启摆竖直，之后再进一步切换为LQR等反馈控制系统保证自己的稳定。
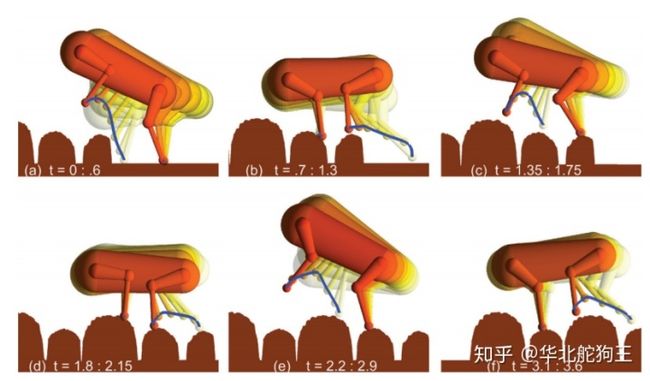
综上，状态反馈控制主要是保证系统自身的镇定，而为了精确跟踪期望的状态轨迹需要进一步增加状态切换前馈和误差积分反馈部分，从而构建一个完整的闭环控制系统，而对于倒立摆启摆等问题需要采用轨迹规划的方式来实现，在系统依据规划的开环控制量达到稳定状态附近后进一步完成反馈状态的切换，这样的规划+反馈控制思想被大量应用于机器人控制中，如四足机器人要实现后空翻、Bound步态跨越障碍物或者跳跃越障，这些复杂的运动控制在不采用AI方法的前提下只能通过采用规划的方法产生期望的足底力作为系统前馈进一步在状态反馈的补偿下实现，否则如果采用传统状态机策略的方法，除了逻辑十分复杂外，控制输出也无法保证满足物理执行器约束，也没法保证最优。
2. 单级倒立摆-启摆轨迹规划
对于传统的机器人控制系统来说规划是其中一个非常重要的环节，如果想研究该问题可以参考论文《An Introduction to Trajectory Optimization: How to Do Your Own Direct Collocation》和相关例程，里面全面地介绍了轨迹规划相关方法，下面首先以其中最简单的单摆启摆为例进行介绍：
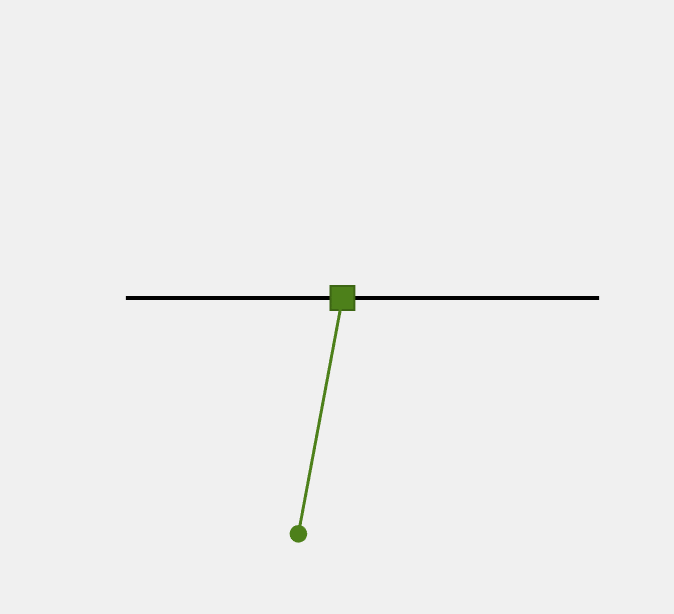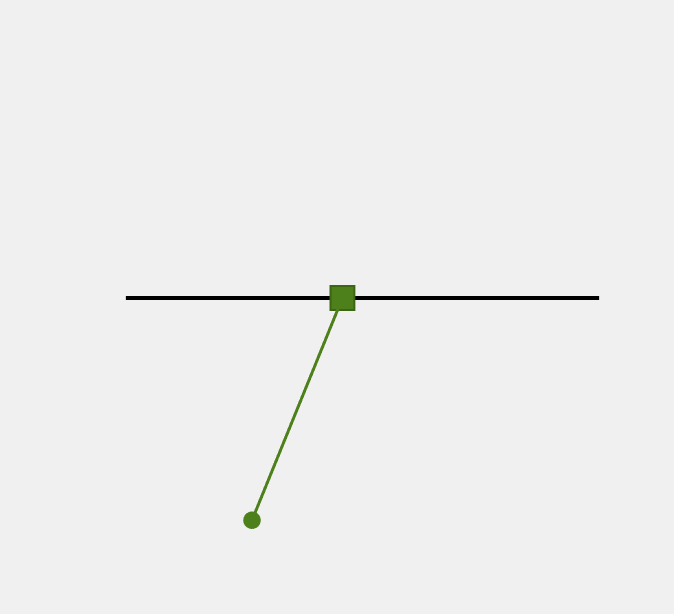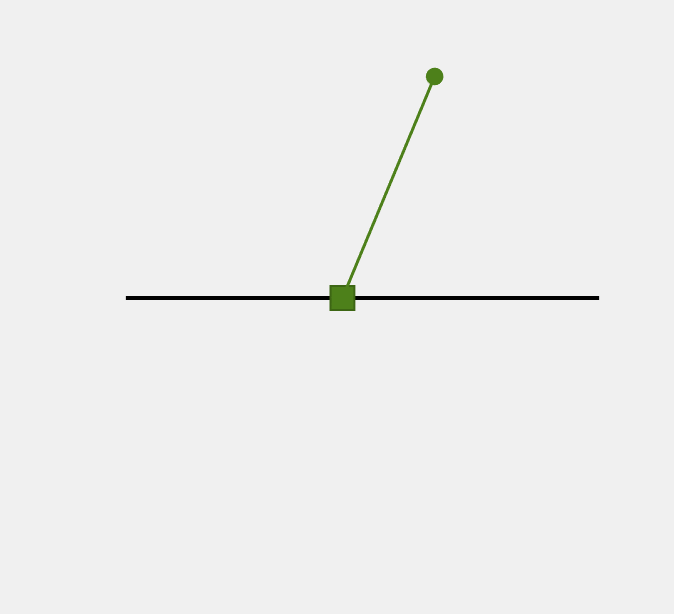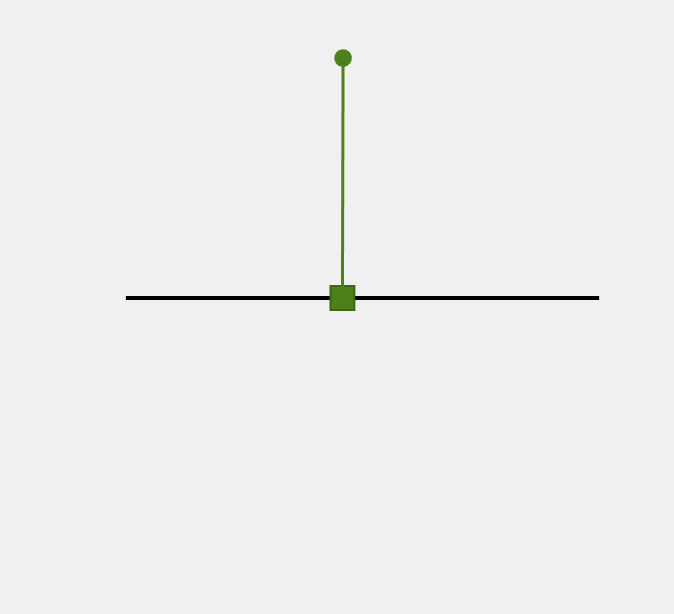
OptimTraj -- Trajectory Optimization Libraryww2.mathworks.cn
对于上述倒立摆模型可以采用Matlab中的优化工具进行建模，首先推导出系统状态对应的微分方程，这里采用拉格朗日法求解，系统控制输入为电机角加速度。
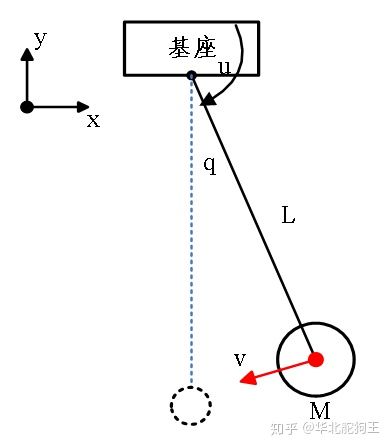
首先求取系统的动能T，对于末端速度可以由角速度计算得到V=dq*L，则有：
对于系统势能，定义锤摆最下端为0势能位置，则对应系统势能H为：
因此拉格朗日函数L为：
求取拉格朗日方程第一部分：
第二部分：
则有：
即：
则基于上述微分动力学，以最小控制输入和系统模型为约束来求解最优启摆轨迹：
这里采用Matlab优化库OptimTraj 来进行离线求解，首先构建系统的微分动力学模型：
function dx = dynamics2(x,u,p)%单摆微分动力学
q = x(1,:);
dq = x(2,:);
m = p.m; l = p.l; g=9.8;
ddq = (u-m*9.8*l*sin(q))/(m*l^2);%u为角角速度输入
dx = [dq;ddq];
End定义系统模型与优化目标函数：
problem.func.dynamics = @(t,x,u)( dynamics2(x,u,p) );
problem.func.pathObj = @(t,x,u)( u.^2 );%优化约束定义时间约束，起始状态时间为0，末端时间约束最大2.5s最小0.5s：
problem.bounds.initialTime.low = 0;
problem.bounds.initialTime.upp = 0;
problem.bounds.finalTime.low = 0.5;
problem.bounds.finalTime.upp = 2.5;%时间约束对各系统状态进行物理限制：
problem.bounds.state.low = [-2*pi; -inf];
problem.bounds.state.upp = [2*pi; inf];设定初始状态，为垂下：
problem.bounds.initialState.low = [-0/57.3;0];%初始状态垂下
problem.bounds.initialState.upp = [-0/57.3;0];给定末端状态，为竖直：
problem.bounds.finalState.low = [pi;0];%末端竖直状态
problem.bounds.finalState.upp = [pi;0]; 对控制输入进行约束：
problem.bounds.control.low = -10; %-inf; %力矩输入
problem.bounds.control.upp = 10; %inf;给定轨迹的初值，这里采用参考文献中使用的线性插值方法：
problem.guess.time = [0,1];
problem.guess.state = [0, pi; pi, pi];
problem.guess.control = [0, 0];在选择梯形优化方法trapezoid后进行求解soln = optimTraj(problem)，最终绘制曲线：
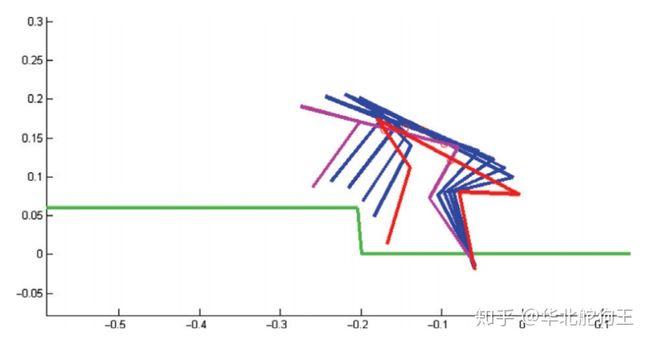
综上，基于轨迹规划结果我们可以获取系统的各阶状态，使用轨迹各时刻的角度和角速度构建反馈控制，使用规划的控制输入u作为前馈，完成对启摆轨迹的跟踪，当达到最高点时切换为LQR等闭环反馈系统从而实现启摆到自稳的完整控制流程。
基于该方法我们可以向更复杂的模型进行拓展。
3. Cart-Pole小车倒立摆-启摆轨迹规划
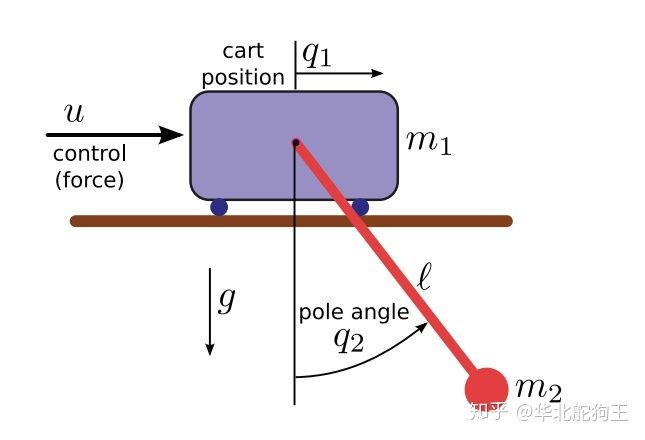
下面给出了Cart-Pole小车倒立摆模型，其是一个最典型的一阶倒立摆系统，相比单摆系统状态维度和模型复杂度都更高，其被广泛应用于控制理论研究，同时也是目前很多强化学习算法喜欢用来验证神经网络和训练方法的对象：
对于上述模型的建模目前网上有很多现成的例子参考，可以采用传统牛顿欧拉法，也可以使用拉格朗日法，另外也推荐如下的线性控制系统学习网站，里面给出了很多典型被控对象的模型建模、开环模型分析、模型离散化线性化以及控制器设计的方法，这里直接给出参考文献中的微分动力学方程：
https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=SystemModelingctms.engin.umich.edu
最终可以构建如下的系统状态矢量和对应模型：
同理，采用之前的优化方法首先构建对应的系统模型函数：
function [ddx,ddq] = autoGen_cartPoleDynamics(q,dq,u,m1,m2,g,l)
%AUTOGEN_CARTPOLEDYNAMICS
% [DDX,DDQ] = AUTOGEN_CARTPOLEDYNAMICS(Q,DQ,U,M1,M2,G,L)
% This function was generated by the Symbolic Math Toolbox version 6.2.
% 24-Nov-2015 15:13:31
t2 = cos(q);
t3 = sin(q);
t4 = t2.^2;
t5 = m1+m2-m2.*t4;
t6 = 1.0./t5;
t7 = dq.^2;
ddx = t6.*(u+g.*m2.*t2.*t3+l.*m2.*t3.*t7);%加速度系统方程
if nargout > 1%nargout指出了输出参数的个数（nargin指出了输入参数的个数）
ddq = -(t6.*(t2.*u+g.*m1.*t3+g.*m2.*t3+l.*m2.*t2.*t3.*t7))./l;%角度系统方程
end之后构建对应的动力学模型与约束矩阵：
problem.func.dynamics = @(t,x,u)( cartPoleDynamics(x,u,p) );%定义系统动力学
problem.func.pathObj = @(t,x,u)( u.^2 ); %Force-squared cost function定义代价函数最小控制输入构建时间约束：
problem.bounds.initialTime.low = 0;%起始时间边界条件
problem.bounds.initialTime.upp = 0;
problem.bounds.finalTime.low = duration;%末端时间边界条件
problem.bounds.finalTime.upp = duration;构建始末状态约束：
problem.bounds.initialState.low = zeros(4,1);%给定始末状态约束
problem.bounds.initialState.upp = zeros(4,1);
problem.bounds.finalState.low = [dist;pi;0;0];%末端竖直状态
problem.bounds.finalState.upp = [dist;pi;0;0];采用线性插值构建轨迹初始值：
problem.guess.time = [0,duration];%初始状态 线性分段插值
problem.guess.state = [problem.bounds.initialState.low, problem.bounds.finalState.low];
problem.guess.control = [0,0];最终启动优化函数，获取启摆轨迹规划结果：
下面的代码基于网上开源例子，如需要我修改的代码可通过知乎咨询功能获取！！
4. 轨迹规划总结
综上，规划+反馈控制是传统机器人控制系统设计最主的方法，在很多无人机、四足机器人中仍然可以看到这样的框架，通过规划的方式能实现传统状态策略切换无法实现的复杂行为如后空翻、跳跃等，它是解决多自由度运动规划的有效手段，但是上述的例子还是比较简单可以看到规划求解目前有很多成熟的工具。而在线规划已经有更成熟的技术来实现，因此核心还是如何建立系统模型，对于足式机器人来说其足地约束以及腾空支撑相切换都需要考虑，这也是强化学习之所以备受瞩目的原因，毕竟只需要在仿真环境就能训练出超人技能确实令人兴奋不已！