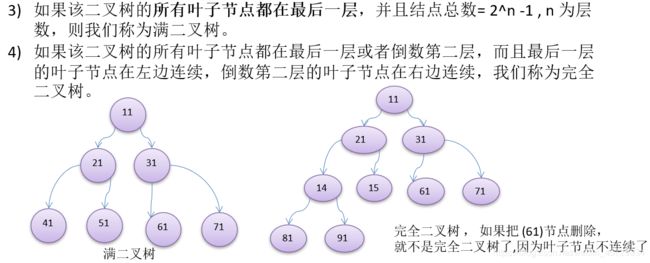
【数算-19】树
文章目录
-
-
- 1、树结构的优点
- 2、树的基本结构与术语
- 3、二叉树简介
-
- 1、二叉树的结构
- 2、二叉树的代码实现
-
- 1、对单个结点的定义(Node.class)
- 2、对二叉树结构的定义(BinaryTree.class)
- 3、二叉树的三种遍历方式
- 4、二叉树遍历实例
-
- 1、先序遍历
- 2、中序遍历
- 3、后序遍历
- 4、对三种遍历方式进行检验
- 5、二叉树的查找
-
- 1、先序查找
- 2、中序查找
- 3、后序查找
- 4、对三种查找方式进行检验
- 5、对三种查找算法的测试及比较
- 6、删除某个节点
-
- 1、问题描述
- 2、代码实现
- 3、代码测试
- 7、删除结点扩展
-
- 1、问题描述
- 2、代码实现
- 3、代码测试
-
1、树结构的优点
- 数组在进行插入删除操作时,会使部分节点进行整体前后移动,造成不必要的开销,但查找效率较链表较高
- 链表在进行查找操作时,每次都要从头结点或首个结点进行遍历,查找效率很低,但插入删除效率较数组而言也较高

- 目前并没有一种数据结构能够较完美地进行各种数据操作,因此树产生了
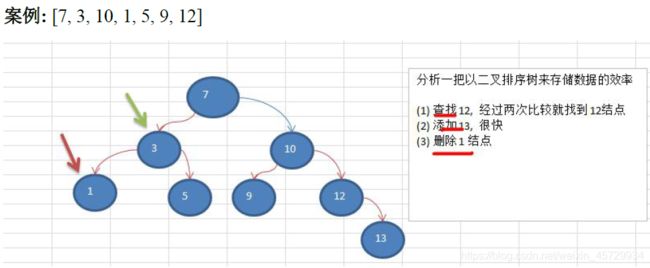
2、树的基本结构与术语
3、二叉树简介
1、二叉树的结构
2、二叉树的代码实现
1、对单个结点的定义(Node.class)
public class Node {
private Integer no;
private String name;
// 分别定义二叉树的左、右子结点
private Node left;
private Node right;
public Node(Integer no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "binary_tree.Node{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
public Integer getNo() {
return no;
}
public void setNo(Integer no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
2、对二叉树结构的定义(BinaryTree.class)
public class BinaryTree {
private Node root;
public BinaryTree(Node root) {
this.root = root;
}
}
3、二叉树的三种遍历方式
二叉树采用哪种遍历主要取决于其根结点遍历顺序:
- 先序遍历:根-左-右
- 中序遍历:左-根-右
- 后序遍历:左-右-根
因此“先”、“中”、“后”针对的是根节点
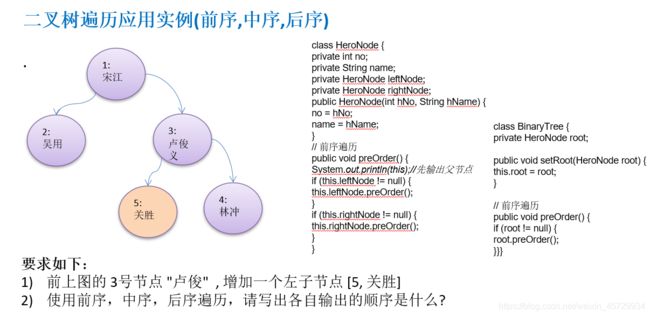
4、二叉树遍历实例
遍历是根据某个节点的左右指针进行相应操作,因此具体的遍历方法应该定义在Node.class中,而方法的调用应该具体针对的是某个点,因此需要在BinaryTree.class中对该方法进行再次封装
1、先序遍历
Node.class
public void preOrderIterate() {
// 不用判断该节点是否为空
// 直接先打印当前节点
System.out.println(this);
// 对当前节点的左子节点进行递归遍历
if (this.left != null) {
this.left.preOrderIterate();
}
// 递归遍历当前节点的右子节点
if (this.right != null) {
this.right.preOrderIterate();
}
}
BinaryTree.class
public void preIterate() {
if (this.root != null) {
this.root.preOrderIterate();
} else {
System.out.println("当前根节点为空!");
}
}
2、中序遍历
Node.class
public void midOrderIterate() {
if (this.left != null) {
this.left.midOrderIterate();
}
System.out.println(this);
if (this.right != null) {
this.right.midOrderIterate();
}
}
BinaryTree.class
public void midIterate() {
if (this.root != null) {
this.root.midOrderIterate();
} else {
System.out.println("当前根节点为空!");
}
}
3、后序遍历
Node.class
public void postIterate() {
if (this.left != null) {
this.left.postIterate();
}
if (this.right != null) {
this.right.postIterate();
}
System.out.println(this);
}
BinaryTree.class
public void postIterate() {
if (this.root != null) {
this.root.postIterate();
} else {
System.out.println("当前根节点为空!");
}
}
4、对三种遍历方式进行检验
public class BinaryTreeTest {
public static void main(String[] args) {
Node root = new Node(1,"宋江");
Node node1 = new Node(2,"吴用");
Node node2 = new Node(3,"卢俊义");
Node node3 = new Node(4,"林冲");
Node node4 = new Node(5,"阮小七");
Node node5 = new Node(6,"阮小五");
Node node6 = new Node(7,"阮小六");
BinaryTree binaryTree = new BinaryTree(root);
root.setLeft(node1);
root.setRight(node2);
node1.setRight(node4);
node2.setRight(node3);
// 1
// / \
// 2 3
// \ \
// 5 4
System.out.println("前序遍历");
binaryTree.preIterate();
System.out.println("----");
System.out.println("中序遍历");
binaryTree.midIterate();
System.out.println("----");
System.out.println("后序遍历");
binaryTree.postIterate();
}
}
5、二叉树的查找
二叉树的查找也分为三种:先序查找、中序查找及后序查找
1、先序查找
Node.class
// 前序查找
public Node preSearch(int value) {
System.out.println("~~~"); //用来显示递归次数
// 先比较当前节点是否为指定值
if (this.getNo() == value) {
return this;
}
// 若当前节点不为指定值,则判断当前节点的左子节点是否为空,若不为空,则递归前序查找
// 若做递归前序查找,找到节点则返回
Node resNode = null; //创建resNode用来接收no为value的节点
if(this.left!=null) {
resNode = this.left.preSearch(value);
}
if(resNode!=null){
//判断结果集不为空,说明找到,直接返回,避免左子树找到还要去右子树寻找
return resNode;
}
// 若左子树没找到,就去右子树找
if(this.right!=null){
resNode = this.right.preSearch(value);
}
// 直接返回结果集即可
return resNode;
}
BinaryTree.class
public Node preSearch(int value){
if(this.root!=null){
return root.preSearch(value);
}else{
System.out.println("二叉树为空,无法遍历");
return null;
}
}
2、中序查找
Node.class
// 中序查找
public Node midSearch(int value){
Node resNode = null; //创建resNode用来接收no为value的节点
if(this.left!=null) {
resNode = this.left.midSearch(value);
}
if(resNode!=null){
//判断结果集不为空,说明找到,直接返回
return resNode;
}
System.out.println("~~~");
if(this.getNo()==value){
return this;
}
if(this.right!=null){
resNode = this.right.midSearch(value);
}
return resNode;
}
BinaryTree.class
public Node midSearch(int value){
if(this.root!=null){
return root.midSearch(value);
}else{
System.out.println("二叉树为空,无法遍历");
return null;
}
}
3、后序查找
Node.class
// 后序查找
public Node postSearch(int value){
Node resNode = null;
if(this.left!=null){
resNode = this.left.postSearch(value);
}
if(resNode!=null){
return resNode;
}
if(this.right!=null){
resNode = this.right.postSearch(value);
}
if(resNode!=null){
return resNode;
}
System.out.println("~~~");
if(this.getNo()==value){
return this;
}
return resNode;
}
BinaryTree.class
public Node postSearch(int value){
if(this.root!=null){
return root.postSearch(value);
}else{
System.out.println("二叉树为空,无法遍历");
}
return null;
}
4、对三种查找方式进行检验
public class BinaryTreeTest {
public static void main(String[] args) {
Node root = new Node(1,"宋江");
Node node1 = new Node(2,"吴用");
Node node2 = new Node(3,"卢俊义");
Node node3 = new Node(4,"林冲");
Node node4 = new Node(5,"阮小七");
Node node5 = new Node(6,"阮小五");
Node node6 = new Node(7,"阮小六");
BinaryTree binaryTree = new BinaryTree(root);
root.setLeft(node1);
root.setRight(node2);
node1.setRight(node4);
node2.setRight(node3);
// 1
// / \
// 2 3
// \ \
// 5 4
System.out.println("前序查找");
binary_tree.Node resNode1 = binaryTree.preSearch(5);
if(resNode1!=null){
System.out.printf("找到了no=%d,name = %s的结点\n",resNode1.getNo(),resNode1.getName());
}else{
System.out.println("找不到");
}
System.out.println("----");
System.out.println("中序查找");
binary_tree.Node resNode2 = binaryTree.midSearch(5);
if(resNode2!=null){
System.out.printf("找到了no=%d,name = %s的结点\n",resNode2.getNo(),resNode2.getName());
}else{
System.out.println("找不到");
}
System.out.println("----");
System.out.println("后序查找");
binary_tree.Node resNode3 = binaryTree.postSearch(5);
if(resNode3!=null){
System.out.printf("找到了no=%d,name = %s的结点\n",resNode3.getNo(),resNode3.getName());
}else{
System.out.println("找不到");
}
}
}
5、对三种查找算法的测试及比较
根据上述代码,以及对递归进行了标识,可以看到对于5号结点来说,前序查找共调用方法3次,中序为2次,后序为1次

6、删除某个节点
1、问题描述
2、代码实现
Node.class
// 删除指定序号的结点
/*
思路:因为二叉树是单向的,所以在调用方法时判断的是当前节点的子节点是否需要删除而不是当前结点是否需要删除
若当前节点的左子节点不为空且no为value,则直接将其左子节点置为空并返回 this.left = null
右子节点同理 this.right = null
若左右子节点均不是要删除的结点,则递归调用其左右子节点的该方法进行判断删除操作
*/
public void delNode(int no){
// 判断该节点的左右结点是否为待删除结点
// 左子树不为空且其值等于no
if(this.left != null &&this.left.getNo()==no){
this.left = null;
}
// 右子树不为空且其值等于no
if(this.right!=null&&this.right.getNo()==no){
this.right = null;
}
// 分别递归左右子树
if(this.left!=null){
this.left.delNode(no);
}
if(this.right!=null){
this.right.delNode(no);
}
}
BinaryTree.class
// 删除节点
public void delNode(int no){
if(this.root!=null){
// 如果只有一个root节点,就需要判断root是不是待删除结点
if(this.root.getNo()==no){
root = null;
}else{
root.delNode(no);
}
}else{
System.out.println("树为空,不能删除!");
}
}
3、代码测试
测试类
public class BinaryTreeTest {
public static void main(String[] args) {
Node root = new Node(1,"宋江");
Node node1 = new Node(2,"吴用");
Node node2 = new Node(3,"卢俊义");
Node node3 = new Node(4,"林冲");
Node node4 = new Node(5,"阮小七");
Node node5 = new Node(6,"阮小五");
Node node6 = new Node(7,"阮小六");
BinaryTree binaryTree = new BinaryTree(root);
root.setLeft(node1);
root.setRight(node2);
node1.setLeft(node3);
node2.setRight(node4);
node4.setLeft(node5);
node4.setRight(node6);
System.out.println("删除no为3的结点");
System.out.println("删除前");
root.preOrderIterate();
root.delNode(3);
System.out.println("删除后:");
root.preOrderIterate();
}
}
7、删除结点扩展
1、问题描述
2、代码实现
Node.class
/*
* 扩展:
* 若删除的是非叶子结点且该结点只有一个子节点,那么就让其子节点代替该叶子结点的位置
* 若删除的是非叶子结点且该结点有两个子节点,让其左子节点代替该叶子结点的位置
* */
public void delNode(int no){
// 判断该节点的左右结点是否为待删除结点
if(this.left!=null&&this.left.getNo()==no){
if(this.left.left!=null&&this.left.right==null){
this.left = this.left.left;
}
if(this.left.right!=null&&this.left.left==null){
this.left = this.left.right;
}
if(this.left.left !=null && this.left.right!=null){
// 删除的是非叶子结点且该结点有两个子节点,让其左子节点代替该叶子结点的位置,当前节点的右子节点变为当前节点左子节点的右子节点
this.left.left.setRight(this.left.right);
this.left = this.left.left;
}
// this.left = null;
}
if(this.right!=null&&this.right.getNo()==no){
if(this.right.left!=null&&this.right.right==null){
this.right = this.right.left;
}
if(this.right.right!=null&&this.right.left==null){
this.right = this.right.right;
}
if(this.right.left!=null&&this.right.right!=null){
// 删除的是非叶子结点且该结点有两个子节点,让其左子节点代替该叶子结点的位置,当前节点的右子节点变为当前节点左子节点的右子节点
this.right.left.setRight(this.right.right);
this.right = this.right.left;
}
// this.right = null;
}
// 分别递归左右子树
if(this.left!=null){
this.left.delNode(no);
}
if(this.right!=null){
this.right.delNode(no);
}
}
BinaryTree.class
// 删除节点
public void delNode(int no){
if(this.root!=null){
// 如果只有一个root节点,就需要判断root是不是待删除结点
if(this.root.getNo()==no){
root = null;
}else{
root.delNode(no);
}
}else{
System.out.println("树为空,不能删除!");
}
}
3、代码测试
对于扩展问题的两个要求:
/*
* 扩展:
* 若删除的是非叶子结点且该结点只有一个子节点,那么就让其子节点代替该叶子结点的位置
* 若删除的是非叶子结点且该结点有两个子节点,让其左子节点代替该叶子结点的位置
* */
针对只有一个子节点的结点,可以删除node3(no=2)
public class BinaryTreeTest {
public static void main(String[] args) {
Node root = new Node(1,"宋江");
Node node1 = new Node(2,"吴用");
Node node2 = new Node(3,"卢俊义");
Node node3 = new Node(4,"林冲");
Node node4 = new Node(5,"阮小七");
Node node5 = new Node(6,"阮小五");
Node node6 = new Node(7,"阮小六");
BinaryTree binaryTree = new BinaryTree(root);
root.setLeft(node1);
root.setRight(node2);
node1.setLeft(node3);
node2.setRight(node4);
node4.setLeft(node5);
node4.setRight(node6);
System.out.println("删除no为2的结点");
System.out.println("删除前");
root.preOrderIterate();
root.delNode(2);
System.out.println("删除后:");
root.preOrderIterate();
}
}
针对两个子节点的节点,可以删除node6(no=5)
public class BinaryTreeTest {
public static void main(String[] args) {
Node root = new Node(1,"宋江");
Node node1 = new Node(2,"吴用");
Node node2 = new Node(3,"卢俊义");
Node node3 = new Node(4,"林冲");
Node node4 = new Node(5,"阮小七");
Node node5 = new Node(6,"阮小五");
Node node6 = new Node(7,"阮小六");
BinaryTree binaryTree = new BinaryTree(root);
root.setLeft(node1);
root.setRight(node2);
node1.setLeft(node3);
node2.setRight(node4);
node4.setLeft(node5);
node4.setRight(node6);
System.out.println("删除no为5的结点");
System.out.println("删除前");
root.preOrderIterate();
root.delNode(6);
System.out.println("删除后:");
root.preOrderIterate();
}
}