【C++】算法集锦(2):递归精讲
文章目录
-
- 前言
- 从“楼梯事件”说起
-
- 解决方案
- 自下而上
-
- 记忆化
- 代码实现
- 递归的解题步骤
- 递归精练
-
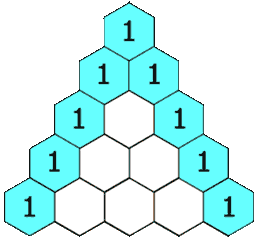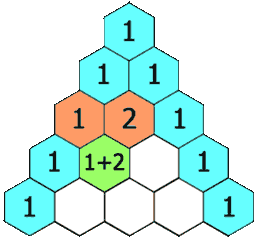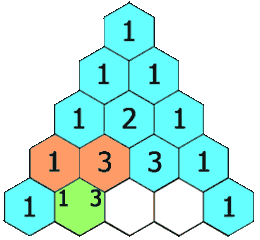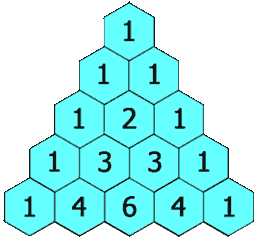
- 1、打印杨辉三角的第k行
-
- 代码实现:
- 2、合并两个有序链表
-
- 代码实现:
- 3、快速排序
-
- 双边遍历
- 单边遍历
- 双边循环代码实现
- 2、单边循环代码实现
前言
之前是写过一篇“递归”的博客,但是感觉有点水,例题没有给到位,细节也没有点明白,所以今天再写一遍,前面那篇就删了吧。
从“楼梯事件”说起
在这个古老的国度,流传着一个经久不衰的问题:爬楼梯问题。
在你面前,有N层楼梯,对于你来说,一次只能爬一层或两层楼梯。试问,你知道自己有多少种不同的方法爬上这N层楼梯吗?
解决方案
如果你的第一反应是暴力枚举,那是很正常的。因为我还没学递归的时候也是想着暴力枚举,但是枚举到后面就会发现行不通了。
不过,再没有办法的情况下,也只能暴力枚举,枚举一下,找出规律
先看4层楼梯的情况:
1(1) 1(2) 1(3) 1(4)
1(1) 1(2) 2(4)
1(1) 2(3) 1(4)
2(2) 1(3) 1(4)
2(2) 2(4)
括号中是爬完之后的具体层数。
我们可以发现,要一步登顶的楼层,有且仅有:2层,或者3层。
那也就是说,到达顶层(N)的方法数,就是到达(N-1)层和到达(N-2)层方法数的和。
那要怎么知道到达(N-1)层和到达(N-2)层的方法数呢?
往下递推,到达(N-1)层的方法数就是到达(N-2)层和(N-3)层方法数的和。
递推到什么时候结束呢,递归到某一层的方法数可以唯一确定的时候,比方说递推到了1层和2层。
令 dp[i] 表示能到达第 i 阶的方法总数:
dp[i]=dp[i−1]+dp[i−2]
自下而上
我看到好多地方都在说什么,自上而下,自下而上,是吧。
这个递归问题呢,我们采用自下而上的方式。为什么呢?
假设现在有10层台阶,那么自上而下的递归方式是:
10层
8层+9层
6层+7层+7层+8层
4层+5层+5层+6层+5层+6层+6层+7层
···
这些层数,都不用去储存的吗?
在递归中,每一层的状态都要存储到栈空间中
我试过30层这样递归下去,栈空间直接爆了。
记忆化
那又什么办法来消除这些重复项呢?有的。采用递归记忆化的方式,也就是备忘录模式。
为了消除上述情况中的重复计算,其中一个想法是将中间结果存储在缓存中,以便我们以后可以重用它们,而不需要重新计算。
这个想法也被称为记忆化,这是一种经常与递归一起使用的技术。
我们可以使用哈希表来跟踪每个以 n 为键的 F(n) 的结果。 散列表作为一个缓存,可以避免重复计算。 记忆化技术是一个很好的例子,它演示了如何通过增加额外的空间以减少计算时间。
现在,我们只需要存储30个递归栈了。
这就是最优方案了吗?很显然,并不是,我们还可以精益求精。
如果说,4层 = 3层+2层,那我们为什么不给它倒过来呢?
1层+2层 = 3层
2层+3层 = 4层
···
这是斐波那契数列,在这里,也不需要啥记忆化了,咱只需要储存两个节点就行了,又快。
所以最后的代码实现为:
代码实现
int climbStairs(int n) {
if(n == 1)
return 1;
int n1 = 1,n2 = 2;
int temp = n2;
while(n>2){
temp = n1+temp;
n1 = n2;
n2 = temp;
n--;
}
return temp;
}
递归的解题步骤
当你的技术已经炉火纯青的时候,自然是可以一眼就看出其中的递推关系式。
但现实是我们很多人还没到那个水平。
所以还是老老实实的一步一步来吧。
1、明确你要干嘛
2、明确递归的结束条件
3、寻找递推关系式
4、注意边界条件与调用方式
递归精练
1、打印杨辉三角的第k行
代码实现:
vector<int> getRow(int rowIndex) {
vector<int> ret(rowIndex+1,0);
ret[0] = 1;
if (rowIndex == 0)
return ret;
for (int j = 1; j <= rowIndex; j++) {
for (int i = j-1; i >0; i--) {
ret[i] = ret[i - 1] + ret[i];
}
ret[j] = 1;
}
return ret;
}
2、合并两个有序链表
如题。
代码实现:
ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == NULL) {
return l2;
}
else if (l2 == NULL) {
return l1;
}
else if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
}
else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
3、快速排序
双边遍历
这个方法呢,如果对快慢指针和双指针不是很了解的朋友可以现在了解一下。
![]()
首先啊,确定基准为4,左指针指向第一个元素,右指针指向尾巴。
![]()
右指针开始,向前遍历,找到第一个大于基准的元素就停下,轮到左指针,同理。
当两个指针都停下之后,将两个指针所指向的值互换位置。
![]()
重复上述步骤直到左右指针重合。
重合之后,将基准元素与左右指针当前位置元素进行互换。
一次循环之后,重复上述动作,对划分出的部分再次循环,直到每个部分都只有一个元素为止。
单边遍历
这个是快慢指针实现。
![]()
这个mark,是慢指针。快指针没标出来。,依旧找好了基准,快指针从慢指针后一位开始快速遍历,直到遍历到小于基准元素的元素时停滞。
![]()
将慢指针前移一位,将当前快慢指针位置元素互换(如果重叠就算了)。然后快指针继续向后走。
![]()
重复上述步骤直到左右指针重合。
重合之后,将基准元素与左右指针当前位置元素进行互换。
一次循环之后,重复上述动作,对划分出的部分再次循环,直到每个部分都只有一个元素为止。
双边循环代码实现
#include2、单边循环代码实现
void oneSideSort(vector<int>& vec1, int slow, int hight)
{
//设置退出条件
if (slow >= hight)
return;
//将标志位留住
int flag = vec1[slow];
int keep_slow = slow;
int keep_hight = hight;
//使用快指针遍历,将小于标志位的前移
for (int quick = slow + 1; quick <= hight; quick++)
{
if (vec1[quick] < flag)
{
slow++;
int change_temp = vec1[slow];
vec1[slow] = vec1[quick];
vec1[quick] = change_temp;
}
}
vec1[keep_slow] = vec1[slow];
vec1[slow] = flag;
oneSideSort(vec1, keep_slow,slow-1);
oneSideSort(vec1,slow+1, keep_hight);
}
int main()
{
vector<int> vec1 = {
2,1,2,3}; //测试用2个数测试最直观,因为最后都要通过这一步才能正常
int left = 0;
int right = vec1.size() - 1;
oneSideSort(vec1, left, right);
for (; left <= right; left++)
cout << vec1[left] << " ";
cout << endl;
return 0;
}