时间序列分析之:傅里叶变换找周期
时间序列分析
万万没想到吧,信号处理的技术,能用在数据分析中。谁叫我是学通信出生的呢?
承接上一篇:函数分解
本节承接上文找函数的周期。
文章目录
- 时间序列分析
- 傅里叶变换
- 一、傅里叶变换(FFT)是什么?
- 二、使用步骤
-
- 1.新建FFT函数
- 2.测试函数
- 总结
傅里叶变换
通信专业的我,看到找周期时,不由自主想起了傅里叶变换。
傅里叶变换就是把时域上的信号,变换到频域上,用很多个正弦波来合成时域信号。所以,我们找信号幅度最大的那个正弦波的频率,作为函数的周期。
傅里叶变换最详细的介绍见这个文:详细得令人发指
一、傅里叶变换(FFT)是什么?
世间万物都在随着时间不停的改变,并且永远不会静止下来。比如一个周期变化的函数,但如果我告诉你,用另一种方法来观察世界,你会发现世界是永恒不变的,这个静止的世界就叫做频域。
比如一年四季每天都在变化,但是变化的频率却永远都是12个月。所以在频率的视角看,四季更迭就是固定的12个月。
我们知道经济有周期,那么周期是多少呢?傅里叶变换让我们站在频率的角度看,就更加直观。
二、使用步骤
1.新建FFT函数
功能:把函数进行傅里叶变换,变换到频域,以期获得函数的周期。
然后我们只用找到局部增幅最大的那个正弦波作为周期。
比如下图的上半部分是我们观察到的实际信号,下半部分进行了傅里叶变换,得到了他的频率为10,相对于上面一直变化的曲线,下面频率的图,只有在10的位置有一个波动点,其余都是0,所以是相对静止的。我们可以说,上半部分的图形的频率为10,根据总计的1000个输入点,因此这个图形的周期是100,也就是100个采样点就是一个完整周期。:

新建的fft代码如下(示例):
# 功能:把函数进行傅里叶变换,变换到频域,以期获得函数的周期
# 输入:时间序列,获取频率点数值n(可选),频率对应幅度的下限值fmin(可选)
# 输入序列的X轴需要归一化为1
# 输出: n个序列的下标以及对应的幅度值
# 创建时间: 2021-1-26
import pandas as pd
import numpy as np
import math
import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt
import seaborn
import scipy.signal as signal
def fftTransfer(timeseries, n=10, fmin=0.2):
yf = abs(fft(timeseries)) # 取绝对值
yfnormlize = yf / len(timeseries) # 归一化处理
yfhalf = yfnormlize[range(int(len(timeseries) / 2))] # 由于对称性,只取一半区间
yfhalf = yfhalf * 2 # y 归一化
xf = np.arange(len(timeseries)) # 频率
xhalf = xf[range(int(len(timeseries) / 2))] # 取一半区间
plt.subplot(211)
x = np.arange(len(timeseries)) # x轴
plt.plot(x, timeseries)
plt.title('Original wave')
plt.subplot(212)
plt.plot(xhalf, yfhalf, 'r')
plt.title('FFT of Mixed wave(half side frequency range)', fontsize=10, color='#7A378B') # 注意这里的颜色可以查询颜色代码表
fwbest = yfhalf[signal.argrelextrema(yfhalf, np.greater)]
xwbest = signal.argrelextrema(yfhalf, np.greater)
plt.plot(xwbest[0][:n], fwbest[:n], 'o', c='yellow')
plt.show(block=False)
plt.show()
xorder = np.argsort(-fwbest) # 对获取到的极值进行降序排序,也就是频率越接近,越排前
print('xorder = ', xorder)
print(type(xorder))
xworder = list()
xworder.append(xwbest[x] for x in xorder) # 返回频率从大到小的极值顺序
fworder = list()
fworder.append(fwbest[x] for x in xorder) # 返回幅度
if len(fwbest) <= n:
fwbest = fwbest[fwbest >= fmin].copy()
return len(timeseries)/xwbest[0][:len(fwbest)], fwbest #转化为周期输出
else:
fwbest = fwbest[fwbest >= fmin].copy()
print(len(fwbest))
print(xwbest)
return len(timeseries)/xwbest[0][:len(fwbest)], fwbest # 只返回前n个数 #转化为周期输出
2.测试函数
简单的测试就是新建一个模拟信号,然后fft变换,核心代码如下(生成sin(20πx)的信号,对应的频率为10):
xtime = np.arange(0,1000,1)
xnorm = xtime/len(xtime)
queshi = xnorm +1
plt.plot(xtime,queshi)
zouqi = [sin(x*20*math.pi) for x in xnorm]
plt.plot(xtime,zouqi)
signal = zouqi
y= signal
y = pd.Series(y).astype('float')
df_price=y
x , y=fftTransfer(df_price,n=5,fmin = 0.015) #快速傅里叶变换
print('x = ',x)
print('y = ',y)
但是,实际的生活中的信号就像爱情一样复杂,不是简单的一个周期,而是多个周期的叠加。
比如我们产生一个频率逐渐加快的函数,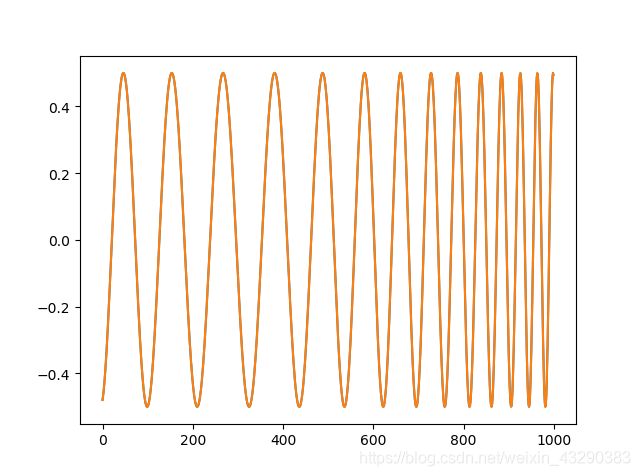
他的周期是多少呢?
首先fft变换到频域:
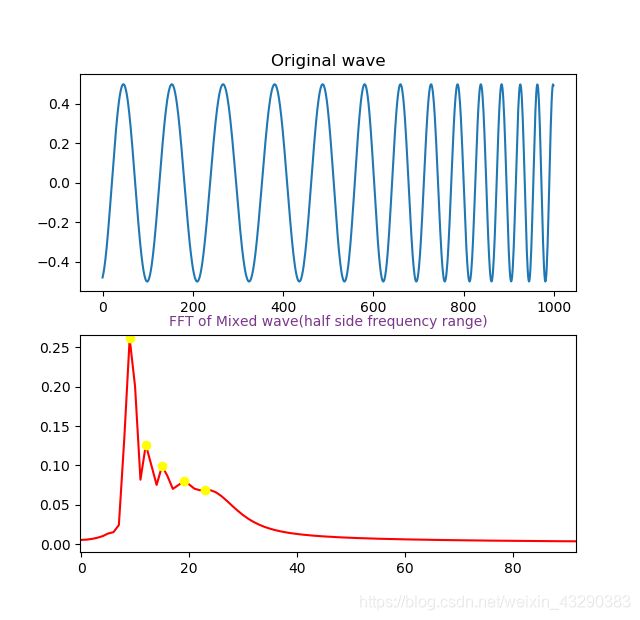
选取增幅最大的5个点,作为周期。
T = [111.11 83.33 66.66 52.63 43.47]
所以可以看出5个周期不同的函数合成。
测试代码如下:
import pandas as pd
import numpy as np
from statsmodels.tsa.seasonal import seasonal_decompose
from dateutil.parser import parse
from math import *
import math
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
import seaborn
from fft import *
import matplotlib.pyplot as plt
xtime = np.arange(0,1000,1)
xnorm = xtime/len(xtime)
queshi = xnorm +1
zouqi = [0.5*sin(x*20*math.pi+2*math.pow(2*x,4)+5*cos(3*x)) for x in xnorm]
#zouqi = [sin(x*20*math.pi) for x in xnorm]
plt.plot(xtime,zouqi)
noize = 0.02*np.random.normal(size=xtime.size)
#plt.plot(xtime,noize)
#signal = queshi+zouqi+noize
signal = zouqi
testx = xtime
y= signal
plt.plot(testx,y)
plt.show()
y = pd.Series(y).astype('float')
y
x , y=fftTransfer(y,n=5,fmin = 0.015) #快速傅里叶变换
print('x = ',x) #周期
print('y = ',y) #周期对应的增幅,也就是权重
这个周期就是我们想要的,在函数分解的时候,需要输入的周期。
总结
通过fft变换确实可以提取到一些周期信息,配合函数分解来使用。
后面我们用创业板指数来试探在现实中是否有意义。