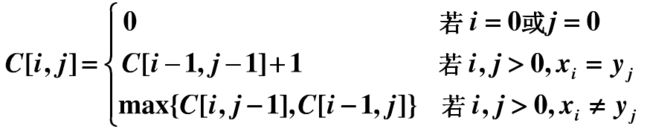算法图解 学习笔记

1.快速排序

import random

def quick_sort(ary):
    #基线条件：为空或者只包含一个元素的数组是"有序"的
    if len(ary)<2:
        return ary
    else:
        print "in...",ary
        pivot=ary[0] #基准值
        less=[]      #所有小于基准值的数值放这
        greater=[]   #所有大于基准值的数值放这
        for i in ary[1:]:
            if i<=pivot:
                less.append(i)
            else:
                greater.append(i)        
        print "pivot=",pivot,"less",less,"greater",greater
        print "out...",less+[pivot]+greater
        return quick_sort(less)+[pivot]+quick_sort(greater)

xList=[]
for i in range(0,10):
    xList.append(random.randint(1,100))
quick_sort(xList)    

in... [44, 35, 79, 61, 37, 68, 64, 7, 89, 79]
pivot= 44 less [35, 37, 7] greater [79, 61, 68, 64, 89, 79]
out... [35, 37, 7, 44, 79, 61, 68, 64, 89, 79]
in... [35, 37, 7]
pivot= 35 less [7] greater [37]
out... [7, 35, 37]
in... [79, 61, 68, 64, 89, 79]
pivot= 79 less [61, 68, 64, 79] greater [89]
out... [61, 68, 64, 79, 79, 89]
in... [61, 68, 64, 79]
pivot= 61 less [] greater [68, 64, 79]
out... [61, 68, 64, 79]
in... [68, 64, 79]
pivot= 68 less [64] greater [79]
out... [64, 68, 79]

2.广度优先算法

广度优先算法可回答两类问题：

1.从节点A触发，有前往节点B的路径吗？

2.从节点A出发，前往节点B的那条路径最短？

例子1：需找芒果销售商

from collections import deque

def person_is_seller(name):
    return name[-1]=='m'

def test_1():
    graph={}
    graph["you"]=["alice","bob","claire"]
    graph["bob"]=["anuj","peggy"]
    graph["alice"]=["peggy"]
    graph["claire"]=["thom","jonny"]
    graph["anuj"]=[]
    graph["peggy"]=[]
    graph["thom"]=[]
    graph["jonny"]=[]
    search_queue=deque()
    search_queue+=graph["you"]
    while search_queue:                 #只要队列不为空
        person=search_queue.popleft()   #就取出其中的第一个人
        if person_is_seller(person):    #检查这个人是否是芒果销售商
            print person+"is a mango seller!";#是芒果销售商
            return True;
        else:
            search_queue+=graph[person] #不是芒果销售商。将这个人的朋友都加入搜索列表
    return False  #如果到了这里，就说明队伍中没有芒果销售商
test_1()

例子1中有人("peggy")检查了两次，做了无用功。因此应该优化一下：

from collections import deque

def person_is_seller(name):
    return name[-1]=='m'

def test_1():
    graph={}
    graph["you"]=["alice","bob","claire"]
    graph["bob"]=["anuj","peggy"]
    graph["alice"]=["peggy"]
    graph["claire"]=["thom","jonny"]
    graph["anuj"]=[]
    graph["peggy"]=[]
    graph["thom"]=[]
    graph["jonny"]=[]
    search_queue=deque()
    search_queue+=graph["you"]
    while search_queue:                 #只要队列不为空
        person=search_queue.popleft()   #就取出其中的第一个人
        if person_is_seller(person):    #检查这个人是否是芒果销售商
            print person+"is a mango seller!";#是芒果销售商
            return True;
        else:
            search_queue+=graph[person] #不是芒果销售商。将这个人的朋友都加入搜索列表
    return False  #如果到了这里，就说明队伍中没有芒果销售商

def test_2():
    graph={}
    graph["you"]=["alice","bob","claire"]
    graph["bob"]=["anuj","peggy"]
    graph["alice"]=["peggy"]
    graph["claire"]=["thom","jonny"]
    graph["anuj"]=[]
    graph["peggy"]=[]
    graph["thom"]=[]
    graph["jonny"]=[]
    search_queue=deque()
    search_queue+=graph["you"]
    searched=[]                         #这个数组用于检测记录过的人
    while search_queue:                 #只要队列不为空
        person=search_queue.popleft()   #就取出其中的第一个人
        if not person in searched:      #仅当这个人没检查过才检查
            if person_is_seller(person):    #检查这个人是否是芒果销售商
                print person+"is a mango seller!";#是芒果销售商
                return True;
            else:
                searched.append(person)   #标记检查过的人
                search_queue+=graph[person] #不是芒果销售商。将这个人的朋友都加入搜索列表
    return False  #如果到了这里，就说明队伍中没有芒果销售商


test_2()

3.狄克斯特拉算法 

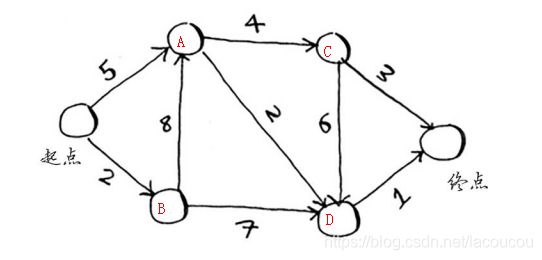
下图中，从起点到终点的最短路径的总权重分别是多少？

 

processed=[]                         #这个数组用于检测记录过的人

def find_lowest_cost_node(costs):
    lowest_cost=float("inf")
    lowest_cost_node=None
    for node in costs:
        cost=costs[node]
        if costnew_cost:
                costs[n]=new_cost
                parents[n]=node
        processed.append(node)
        node=find_lowest_cost_node(costs)
    print "graph",graph
    print "costs",costs
    print "parents",parents


test_3()

//开始

graph {'a': {'c': 4, 'd': 2}, 'c': {'fin': 3, 'd': 6}, 'b': {'a': 8, 'd': 7}, 'd': {'fin': 1}, 'start': {'a': 5, 'b': 2}, 'fin': {}}
costs {'a': 5, 'c': inf, 'b': 2, 'fin': inf, 'd': inf}
parents {'a': 'start', 'c': None, 'b': 'start', 'fin': None, 'd': None}

//运行结束
graph {'a': {'c': 4, 'd': 2}, 'c': {'fin': 3, 'd': 6}, 'b': {'a': 8, 'd': 7}, 'd': {'fin': 1}, 'start': {'a': 5, 'b': 2}, 'fin': {}}
costs {'a': 5, 'c': 9, 'b': 2, 'fin': 8, 'd': 7}
parents {'a': 'start', 'c': 'a', 'b': 'start', 'fin': 'd', 'd': 'a'}

path= fin -> d -> a -> start 
cost: 8

4.贪婪算法 广播台

states_needed=set(["mt","wa","or","id","nv","ut","ca","az"])
stations={}
stations["kone"]=set(["id","nv","ut"])
stations["ktwo"]=set(["wa","id","mt"])
stations["kthree"]=set(["or","nv","ca"])
stations["kfour"]=set(["nv","ut"])
stations["kfive"]=set(["ca","az"])
final_stations=set()
best_station=None
states_covered=set()
#第一步，找到最好的
for station,states_for_station in stations.items():
    covered=states_needed & states_for_station
    #print station
    if len(covered) > len(states_covered):
        best_station=station
        states_covered=covered
        #print best_station,states_covered
#字典是无序的，遍历顺序为 kfive ktwo kthree kone kfour
#所以结果是：ktwo set(['mt', 'id', 'wa'])
print "best_station=",best_station,"states_covered=",states_covered
#第二部，找到全覆盖的
final_stations.add(best_station)
states_needed-=states_covered
while states_needed:
    best_station=None
    states_covered=set()
    for station,states in stations.items():
        covered=states_needed & states
        if len(covered) > len(states_covered):
            best_station=station
            states_covered=covered
            states_needed-=states_covered
            final_stations.add(best_station)
print final_stations

5.动态规划

python二维数组：参考https://www.cnblogs.com/woshare/p/5823303.html

方法1 直接定义

matrix = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]

方法2 间接定义

matrix = [[0 for i in range(3)] for i in range(3)]

最长公共子序列：

https://www.cnblogs.com/Lee-yl/p/9975827.html

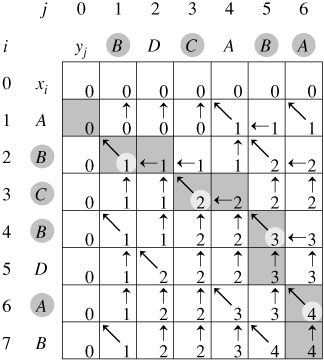
创建 DP数组C[i][j]：表示子字符串L【：i】和子字符串S【：j】的最长公共子序列个数。

def LCS(L,S):
    if not L or not S:
        return ""
    dp = [[0] * (len(L)+1) for i in range(len(S)+1)]
    for i in range(len(S)+1):
        for j in range(len(L)+1):
            if i == 0 or j == 0:
                dp[i][j] = 0
            else:
                if L[j-1] == S[i-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1])
    return dp[-1][-1]
L = 'BDCABA'
S = 'ABCBDAB'
LCS(L,S)

 

def LCS(L,S):
    if not L or not S:
        return ""
    res = ''
    dp = [[0] * (len(L)+1) for i in range(len(S)+1)]
    flag = [['left'] * (len(L)+1) for i in range(len(S)+1)]
    for i in range(len(S)+1):
        for j in range(len(L)+1):
            if i == 0 or j == 0:
                dp[i][j] = 0
                flag [i][j] = '0'
            else:
                if L[j-1] == S[i-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                    flag[i][j] = 'ok'
                else:
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1])
                    flag[i][j] = 'up' if dp[i][j] == dp[i-1][j] else 'left'
    return dp[-1][-1],flag
def printres(flag,L,S):
    m = len(flag)
    n = len(flag[0])
    res = ''
    i , j = m-1 , n-1
    while i > 0 and j > 0:
        if flag[i][j] == 'ok':
            res += L[j-1]
            i -= 1
            j -= 1
        elif flag[i][j] == 'left':
            j -= 1
        elif flag[i][j] == 'up':
            i -= 1
    return res[::-1]            
L = 'BDCABA'
S = 'ABCBDAB'
num,flag = LCS(L,S)
res = printres(flag,L,S)