面试算法之排序算法集锦
排序算法在面试过程中是经常会考的,这是很基础的,面试官觉得你应该很熟悉这些东西,如果你半个小时内写不出来,那基本就给跪了,因为这真的是狠基础狠基础的东西,所以我们得对一些基本的排序算法烂熟于胸,对这些排序思想,效率了如指掌,才能让面试官觉得你还行。基本的排序算法有:直接插入排序,冒泡排序,简单选择排序,shell排序,归并排序,快速排序,堆排序。其中归并,快速,堆排序是面试时候比较喜欢考的,因为这三个排序算法都是很重要的算法,会有很多实际的应用。下面就简单的介绍这些排序算法,并给出代码。
1.直接插入排序
直接插入排序的思想很简单,就是从排序序列开始,依次将每个元素插入到前面已经排序好的序列中,最终使整个序列有序,直接插入排序的时间复杂度O(n^2),空间复杂度为O(1),代码如下:
/**
* Time Complexity:O(n^2)
* Space Complexity:O(1)
*
* sorted data ; array[low...high]
*/
template
void DirectInsertSort(Type array[], int low, int high)
{
if (array == NULL || low >= high || low < 0)
{
return;
}
Type exchange;
int j;
for (int i = low + 1; i <= high; ++i)
{
exchange = array[i];
for (j = i - 1; j >= low; --j)
{
if (exchange < array[j])
{
array[j + 1] = array[j];
}
else
{
break;
}
}
array[j + 1] = exchange;
}
} 2.冒泡排序
我们对冒泡排序应该都比较深,因为这个名字很形象很好记 。排序的思想就是每个冒泡一遍序列,找出一个最大或最小的元素,放到它排序后的位置上直到序列有序。时间复杂度O(n^2),空间复杂度为O(1),代码如下:
/**
* Time Complexity:O(n^2)
* Space Complexity:O(1)
*
* sorted data: array[low...high]
*/
template
void BubbleSort(Type array[], int low, int high)
{
if (array == NULL || low >= high || low < 0)
{
return;
}
Type exchange;
bool change = false;
for (int i = low; i < high; ++i)
{
for (int j = low; j < high - i + low; ++j)
{
if (array[j] > array[j + 1])
{
exchange = array[j + 1];
array[j + 1] = array[j];
array[j] = exchange;
change = true;
}
}
if (!change)
{//如果冒泡过程中没有发生交换,则视序列已经排好序,减少无谓的比较
return;
}
change = false;
}
}
3.简单选择排序
简单选择排序的思想就是每次在未排序的序列中选取一个最小(或最大)的元素,放到最终的位置上,时间复杂度O(n^2),空间复杂度为O(1),代码如下:
/**
* Time Complexity:O(n^2)
* Space Complexity:O(1)
*
* sorted data ; array[low...high]
*/
template
void SelectSort(Type array[], int low, int high)
{
if (array == NULL || low >= high || low < 0)
{
return;
}
int index;
Type exchange;
for (int i = low; i < high; ++i)
{
index = i;
for (int j = i + 1; j <= high; ++j)
{
if (array[j] < array[index])
{
index = j;
}
}
exchange = array[i];
array[i] = array[index];
array[index] = exchange;
}
} 4.折半插入排序
折半插入排序和直接插入排序的差别就是在查找插入位置的方式上,直接插入排序是顺序查找插入位置,折半插入式通过二分搜索的思想来查找插入位置。总体来说直接插入排序的比较次数为1+2+3...+(n-1) ~ O(n^2),二折半查找的比较次数在lg(n-1)+lg(n-2)+...1~O(lg(n!)) ~O(nlgn)(stirling公式)。所以折半查找的优势是减少了比较次数。代码如下:
/**
* Time Complexity:O(n^2)
* Space Complexity:O(1)
* sorted data ; array[low...high]
*/
template
void BinaryInsertSort(Type array[], int low, int high)
{
if (array == NULL || low >= high || low < 0)
{
return;
}
int left, right, mid, j;
Type exchange;
for (int i = low + 1; i <= high; ++i)
{
left = low;
right = i - 1;
while (left <= right)
{
mid = (left + right) / 2;
if (array[i] < array[mid])
right = mid - 1;
else
left = mid + 1;
}
exchange = array[i];
j = i;
while (j > left)
{
array[j] = array[j - 1];
--j;
}
array[left] = exchange;
}
} 5.shell排序
shell排序本身是一种插入排序,它是插入排序的一种改进,排序的思想是:开始按照一定的步长d将序列分成d组,每组内部进行直接插入排序,然后逐步减少步长d,直到步长为1,对整个序列进行一次直接插入排序,使序列最终有序。如下图所示是一个步长为3的初始分组图(取自网络)。
shell排序在开始时步长d较大,分组较多,但每组的元素较少,故各组内直接插入较快,后来步长d逐渐缩小,分组数逐渐减少,而各组的元素数目逐渐增多,但由于之前排过序,使序列较接近于有序状态,所以新的一趟排序过程也较快。因此,shell排序在效率上较直接插人排序有较大的改进。
shell排序很关键的一点就是步长序列的选定,步长序列的选定决定着排序的效率。一般的建议是d(1) = [ n / 2 ],d(i+1) = [ (d(i) - 1) / 3 ],一般认为d都取奇数且互素为好,但这并没有得到理论上的证明。最后一个步长一定为1,这是必然的。
关于shell排序的时间复杂度据说很难分校,理论上没用具体结论,只是提出大致为O(nlgn)~O(n^2)之间,大概为O(n^1.3)。。。下面是代码:
/**
* Time Complexity:between O(nlgn)~O(n^2), about O(n^1.3)
* Space Complexity:O(1)
*
* sorted data ; array[low...high]
*/
template
void ShellSort(Type array[], int low, int high)
{
int gap, len;
Type exhange;
len = high - low + 1;
gap = len / 2;
while(gap >= 1)
{
for (int i = low; i < low + gap; ++i)
{
for (int j = i + gap; j <= high; j += gap)
{
exhange = array[j];
int k = j;
while (k > i && exhange < array[k - gap])
{
array[k] = array[k - gap];
k -= gap;
}
array[k] = exhange;
}
}
if(gap == 2 || gap == 3)
gap = 1;
else
gap = (gap - 1) / 3;
}
} 6.快速排序
快速排序是一个很牛逼的排序算法,在现实中有很多应用,有很多算法都是借鉴快速排序的思想来实现的。虽然快排的最坏时间复杂度为O(n^2),但它的平均性能很好,为O(nlgn)。快排的思想是分治法。每次排序都将序列通过一个主元划分成左右两部分,右部分的元素都比主元大,左边的元素都比主元小,然后分别递归进行左右两部分的排序。快排的主程序结构都如下所示:
/**
* sorted data ; array[low...high]
*/
template
void QuickSort(Type array[], int low, int high)
{
if (low >= high)
{
return;
}
int pivot = QuickSort_Partition(array, low, high);
QuickSort(array, low, pivot - 1);
QuickSort(array, pivot + 1, high);
} 6.1一种简单partition
最简单的一种partition算法如下图所示:选取第一个元素为主元,作为划分的标准(下面几个partition默认同样的选取主元的方法)。
索引i,j初始初始化为序列开始,然后索引j依次后移,如果遇到A[j] <= x,那么就交互A[i + 1]和A[j],直到索引j移动到末尾,这样结果是索引i左侧的元素都<=x,右侧的元素都>x。达到了partition的目的,这种算法很简单,代码如下:
template
int QuickSort_Partition(Type array[], int low, int high)
{
Type pivotData = array[low];
int littleIndex = low;
Type exchange;
for (int largerIndex = low + 1; largerIndex <= high; ++largerIndex)
{
if (array[largerIndex] <= pivotData)
{
++littleIndex;
exchange = array[littleIndex];
array[littleIndex] = array[largerIndex];
array[largerIndex] = exchange;
}
}
exchange = array[littleIndex];
array[littleIndex] = array[low];
array[low] = exchange;
return littleIndex;
} 6.2 Hoare partition
快排的发明者,我们的Hoare爵士,采用的partition算法是,在从序列两端开始扫描,如下图所示:
索引i从左端开始扫描,直到找到第一个大于主元x的元素,索引j从右端开始扫描,直到找到第一个小于等于x的元素,然后将这两个索引对应的元素进行交换。继续上面的操作,直到i > j。代码如下:
template
int QuickSort_Hoare_Partition(Type array[], int low, int high)
{
Type pivotData = array[low];
int littleIndex = low + 1;
int largerIndex = high;
Type exchange;
while (littleIndex <= largerIndex)
{
while(littleIndex <= largerIndex && array[littleIndex] <= pivotData)
++littleIndex;
while(littleIndex <= largerIndex && array[largerIndex] >= pivotData)
--largerIndex;
//through above two while, littleIndex couldn't equal to largerIndex
if (littleIndex < largerIndex)
{
exchange = array[littleIndex];
array[littleIndex] = array[largerIndex];
array[largerIndex] = exchange;
--largerIndex;
++littleIndex;
}
}
array[low] = array[largerIndex];
array[largerIndex] = pivotData;
return largerIndex;
} 6.3 另一种partition
还有一种partition算法,其思想和前面Hoare partition算法类似,都是从两端开始进行双向划分。但是不同的是这种partition两个方向不是同时进行的,相当于半双工的概念,如下图所示:
具体思路:索引i指向主元的位置,索引j先从右端开始向左扫描,直到遇到第一个<= x主元的元素,然后将该元素移动到索引i所指的位置,然后索引i从当前下一个元素开始向右扫描,直到遇到一个>x的元素,将该指辅导索引j所指的位置。如次循环,直到i = j,主元存放到该位置。代码如下:
template
int QuickSort_Another_Partition(Type array[], int low, int high)
{
Type pivotData = array[low];
int littleIndex = low;
int largerIndex = high;
while (littleIndex < largerIndex)
{
while (littleIndex < largerIndex && array[largerIndex] >= pivotData)
--largerIndex;
if (littleIndex < largerIndex)
array[littleIndex++] = array[largerIndex];
while (littleIndex < largerIndex && array[littleIndex] <= pivotData)
++littleIndex;
if (littleIndex < largerIndex)
array[largerIndex--] = array[littleIndex];
}
array[largerIndex] = pivotData;
return largerIndex;
} 6.4随机化快速排序
快速排序最坏情况发生在:每次partition后,分成的序列都是1,i-1两份,即选取的主元是当前序列中最小的元素。这种情况对有序的序列式会发生的。为了尽量防止这种情况的发生,并是快排每次的partition相对均衡,可以采用随机化主元的方法。随机化主元的思想:在每次partition之前,将首元素(当然可以不取首元素作为主元)与序列中其他的任意元素进行交换,用交换后的主元来进行划分。这样就保证快排的运行时间不依赖与输入序列的顺序。代码如下:
template
int QuickSort_Randomized_Partition(Type array[], int low, int high)
{
int randNum = rand()%(high - low + 1) + low;
Type exchange = array[low];
array[low] = array[randNum];
array[randNum] = exchange;
return QuickSort_Partition(array, low, high);
}
template
void QuickSort(Type array[], int low, int high)
{
if (low >= high)
{
return;
}
int pivot = QuickSort_Randomized_Partition(array, low, high);
QuickSort(array, low, pivot - 1);
QuickSort(array, pivot + 1, high);
} 7.归并排序
归并排序和快速排序一样都是很重要的算法,在面试过程中,面试官也是很喜欢考的。归并的思想也是采用分治法,这里所说的归并是采用两路归并,依次将序列从中间划分为两部分,直到序列中元素个数为1,然后进行两两归并,直到最终递归结束。归并排序的时间复杂度是严格的O(nlgn),空间复杂度为O(n)。代码如下:
/**
* Time Complexity:O(nlgn)
* Space Complexity:O(n)
*
* sorted data ; array[low...high]
*/
template
void SubMergeSort(Type *inputArray, Type *tempArray, int lowIndex, int midIndex, int highIndex)
{
int index1 = lowIndex, index2 = midIndex + 1;
int destIndex = lowIndex;
while(index1 <= midIndex && index2 <= highIndex)
{
if(inputArray[index1] < inputArray[index2])
{
tempArray[destIndex++] = inputArray[index1++];
}
else
{
tempArray[destIndex++] = inputArray[index2++];
}
}
//indicate the first half data have move to 'tempArray'
while(index2 <= highIndex)
tempArray[destIndex++] = inputArray[index2++];
//indicate the later half data have move to 'tempArray'
while(index1 <= midIndex)
tempArray[destIndex++] = inputArray[index1++];
for (int i = lowIndex; i <= highIndex; ++i)
{
inputArray[i] = tempArray[i];
}
}
template
void MergeSort_Part(Type *array, Type *tempArray, int low, int high)
{
if (low < high)
{
int mid = (low + high) / 2;
MergeSort_Part(array, tempArray, low, mid);
MergeSort_Part(array, tempArray, mid + 1, high);
SubMergeSort(array, tempArray, low, mid, high);
}
}
template
void MergeSort(Type *array, int len)
{
Type *tempArray = new Type[len];
MergeSort_Part(array, tempArray, 0, len - 1);
delete [] tempArray;
} 8.堆排序
堆排序也是常用排序之一,和快速排序,归并排序可谓是排序三剑客,在面试和实际应用中都随处可见,特别是在大数据处理中。面试中也会结合大数据来考堆排序的。堆排序的思想主要分为两部分:建堆和堆调整。下面以建大根堆为例:
建堆的过程:从第[n / 2]个节点开始依次向下进行筛选,将较大的元素上移,直到堆满足大根堆的要求。实际上建堆的过程是堆调整的过程;
退调整过程:对已经建立的大根堆,输出堆顶元素,然后对剩下的元素进行调整,使其仍然满足大根堆的要求;
堆排序建堆的过程时间复杂度为O(n)(在堆排序中建堆过程的时间复杂度O(n)的证明中已经证明),堆调整过程的时间复杂度为O(nlgn),建立大根堆的代码如下所示:
/**
* Time Complexity:O(nlgn)
* Space Complexity:O(1)
*
* sorted data ; array[low...high]
*/
template
void BigRootHeapAdjust(Type *array, int low, int high)
{
int j, k;
Type temp;
temp = array[low];
k = low;
for (j = low * 2 + 1; j <= high; j = j * 2 + 1)
{
if (j < high && array[j] < array[j + 1])
j += 1;
if (temp > array[j])
break;
array[k] = array[j];
k = j;
}
array[k] = temp;
}
template
void BigRootHeapSort(Type *array, int len)
{
if (array == NULL || len <= 0)
{
return;
}
for (int i = len / 2 - 1; i >= 0; --i)
{
BigRootHeapAdjust(array, i, len - 1);
}
Type exchange;
for (int i = len - 1; i > 0; --i)
{
exchange = array[i];
array[i] = array[0];
array[0] = exchange;
BigRootHeapAdjust(array, 0, i - 1);
}
}
9.计数排序
讲计数排序前,我们首先总结一下前面1~8部分的8种排序算法。看过算法导论的都知道前面的8种排序都被称为比较排序。比较排序:元素的次序是基于排序序列元素的比较。那么对于比较排序的算法存在一个定理:比较排序算法的时间复杂度下限为O(nlgn)。可以通过决策树模型来进行证明,算法导论中有介绍。那么有没有比O(nlgn)更快的算法呢。答案是肯定的,这种算法有很多,都需要特定的技巧。
这里本节介绍一种线性时间复杂度的计数排序算法。计数排序的思想是:建立一个排序序列取值范围大小的数组C,然后根据C的下标,统计序列中每个元素出现的次数,然后累加每个元素之前元素的个数到该元素所在C中。最后根据C得到最后的排序序列。具体代码如下:
/**
* Time Complexity:O(n + range)
* Space Complexity:O(max(n, range))
*
* sorted data: array[low...high]
*/
template
void CountingSort(Type array[], int low, int high, int range)
{
Type *result = new Type[high - low + 1];
Type *valueCount = new Type[range + 1];
for (int i = 0; i <= range; ++i)
{
valueCount[i] = 0;
}
for (int i = low; i <= high; ++i)
{
valueCount[array[i]] += 1;
}
for (int i = 1; i <= range; ++i)
{
valueCount[i] += valueCount[i - 1];
}
for (int i = high; i >= low; --i)
{//form high to low , in order to guarantee the stable sort
result[valueCount[array[i]] - 1] = array[i];
--valueCount[array[i]];
}
int i = low;
while(i <= high)
{
array[i] = result[i - low];
++i;
}
delete [] result;
delete [] valueCount;
} - 如果k < n,T(n) = O(n);
- 否则,如果k < nlgn,T(n) = O(nlgn);
- 否则,如果k > n^2,T(n) = O(n^2);
所以计数排序对输入序列的取值范围限制是很高的,要想在线性时间内完成计数排序,那么排序序列的取值范围k必须小于待排序元素的个数。
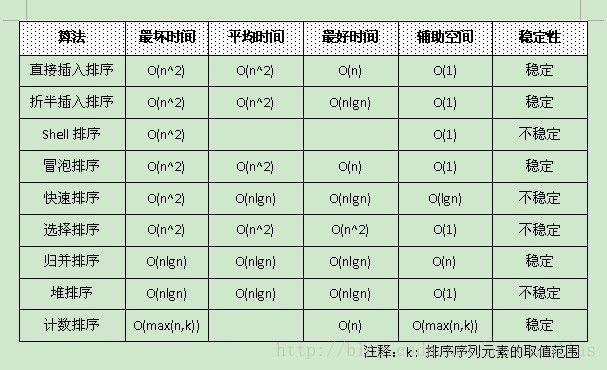
10.各种排序算法性能的比较
下图表是各种排序算法的各种比较,可以很好的进行对比。
对于排序算法可以有以下总结:
- 当排序序列已基本有序时,适合采用直接插入排序和冒泡排序;
- 当排序序列较小时,适合采用选择排序,直接插入,冒泡等简单排序;
- 当排序序列较大时,适合采用shell排序,堆排序,快速排序,归并排序。特别是后面排序三剑客在大数据处理中很常用。
欢迎吐槽。。。
累吐血了。。。碎觉。。。
Creation Date: Sept 11, 2013 AM 03:03@dorm
Last Modification Date: Sept 12, 2013 AM 01:31 @dorm