惩罚因子概念_多因子系列篇一 (上) -- 现代组合理论 (Modern Portfolio Theory)

引言

本质而言，笔者算是一个比较失败的物理专业学生，毕竟没有能够去从事物理这么一门充满魅力的科学，机缘巧合之下，居然到了据说很多物理大牛所在的金融行业，而且能够从事对数学，对建模要求比较高的量化行业，实在是侥幸。

在学习金融量化这块内容的时候，笔者中间也是趟了好多浑水，掉进了好多的坑，总算是误打误撞的，好歹也能去做一些策略的研究。但是，缺乏金融理论基础，缺乏行业研究积累，往往会囿于眼界和思路上，乃至于到目前为止，笔者真正能够熟练研究的，其实还是基于价量数据的一些因子上。

但是实际上，大资金，包括公募、私募、券商自营等，在资产配置与管理上，并不是简单的基于一些价量因子的策略，因此，如果有志于往资管发展，对于资产配置理论确实需要有一个比较系统地学习和研究。

当然，就算不是从事该行业的人，如果对金融感兴趣，想要做一些资产配置，对现在的常用的资产配置理论有个简单了解，也是很有帮助的，至少，在支付宝，微信理财上去寻找合适的基金的时候，也能有一些简单的判断。

在这一块而言，笔者推荐两本书，《主动投资组合管理》和 《量化股票组合管理》。在之后的一系列多因子的文章中，笔者将基于自己的理解，结合一些开源代码实现，去进行一系列的归纳、总结与创新测试，既当做一个系列笔记，也当做一个自我督促成长的记录。

一场著名的赌局，股票组合管理的两种投资理念

2008 年，金融危机爆发前，美国的一家对冲基金老板掏出了 100 万美元，要与巴菲特进行一场赌约。由于巴菲特一直非常推崇被动指数基金，他认为，对于普通投资者而言，投资指数基金完全可以跑赢大部分对冲基金，于是就有了这么一场世纪赌约。

当然，十年之后，巴菲特投资的标普500在十年中获得了7.1%的年化收益率，而对冲基金经理选择的五只对冲基金仅仅获得2.2%年化收益率。巴菲特赢得了赌局。

这么一场著名的赌局，基于对于市场认识的不同理念，即能否通过选股来战胜市场或其他比较基准，引出了股票组合管理的两种方式：主动 和 被动。

主动管理 的基本观点是：通过选股来战胜股票指数或者其他比较基准是可能的，基于这一理念，市场上也确实大浪淘沙，涌现了许多著名的对冲基金，国外比较有名的对冲基金包括 文艺复兴，Two Sigma, D.E.Shaw & Co.，而国内比较有名的包括幻方、九坤等。

被动管理 的基本观点是：组合投资经理并不能战胜市场。被动管理，也被称为指数化管理，主要是尽可能跟踪一个股票指数 (譬如标普 500) 或其他比较基准，不同指数基金由于基金经理对指数复制能力的差异，会有所差异。

当然，除了对市场认知方式差异导致的不同的股票管理配置的不同外，对于组合管理的方式差异，股票组合管理又可以分为 定性 和 定量 两种方式。

定性管理 在国内市场上曾经占据了主流，其研究重点放在股票的无形特征上，并且通常不使用数学公式或计算机程序来区分 "好股票" 和 "坏股票"。而 定量管理 则是基于统计学与数学，在投资决策中，量化组合投资经理会使用所有可用的与投资相关的数据或可量化的信息。

对于不同的市场的认知差异笔者不做评价，毕竟，无论你如何去理解和认识市场，最终是需要落实到市场上去的，而市场会根据你对市场的认知，给你真金白银的奖励或惩罚。

下面，笔者将按照历史顺序依次介绍 MPT, CAPM 以及 APT 理论，理论其实挺老了，但是，经典不会因为理论提出的远近而褪色，让我们重温一下大牛们对于市场的思考，并基于此，去进一步研究我们的多因子理论与实践。

Modern Portfolio Theory (MPT) 现代组合理论

金融资产配置的目标是将投资资金合理地分配在多种资产上，在将风险控制在一定范围内的同时把收益率最大化。 其中最著名的理论是现代资产配置理论(Modern Portfoilio Theory)，简称 MPT，由 Markowitz 在 1952 年提出。 MPT 的核心思想是以最小化标准差（或同理的，方差）并最大化预期收益为目标来进行资产配置，有时也称为均值-方 差分析 (Mean-Variance Analysis)，是金融经济学的一个重要基础理论。

风险与预期收益

MPT 假设投资者都是风险厌恶者，即在有相同收益的两个资产组合中，投资者一定会选择风险更小的资产组合。同 时，对于风险的描述可以通过资产的收益率波动 (标准差) 进行衡量。

按照 MPT，资产组合的收益来自于资产组合的各个资产的加权之和，而资产组合的波动率 (理解为风险) 则是各个 资产之间相关系数

的函数。

用数学语言表述资产组合的预期收益与风险，可以表示如下：

• 资产组合的预期收益：
• 组合回报方差：
  , 其中，
  是一段时间截面内资产回报的标准差，
  则 表示资产
  与资产
  之间的相关系数。
• 资产回报波动率：

分散投资

从上面的数学公式，可以很容易看出来，分散化投资到相关性不高的资产上，那么相应的资产组合的风险就会比集 中投资的风险更小。

举例而言，如果持有两个风险资产的资产组合，如果两个资产的相关系数

，即意味着两个资 产的相关性很高，另外两个风险资产的资产组合的相关系数

, 即两个资产几乎没有相关性，可以很明显看出，没有相关性的资产组合，其相应的

也会更小，即风险更小。

再换一种通俗的语言来讲，分散投资就是我们中国的古话 "鸡蛋不能放在一个篮子里"。MPT 用数学的方式去重新 讲述了鸡蛋不同篮的道理。

有效前沿概念与推导 （数学警告）

当使用数量化的定义的时候，有些定性的理论，其实可以用数学去给出定量的配置方案，这也是定量化的组合管理 相比定性管理的优势。在对预期收益和风险给出了数学表达式之后，根据我们想要资产配置达到的效果 (固定风险 下，最大化收益；固定收益情况下，最小化风向)，我们完全可以利用最优化理论来求解资产配置中相应的每个资 产的比例。

假设我们有

个风险资产，收益率用

表示，在资产组合中，它们的份额用

表示， 于是有

如果令

, 显然，

作为资产组合中的资 产，应该满足

, 同时，假设可以沽空，即不限制

, 记预期收益 为

, 收益协方差为

, 通过定义，可以比较明显看出，协方差矩阵为半正定矩阵 [^1],

同时，按照之前的定义，对于期望收益

和收益方差，我们有

在给定收益期望

的时候，我们希望能最小化风险

, 或者当给定风险

的时候，我 们希望最大化预期收益

. 对于前一种情况，用数学语言表示即为：

上述最优化问题求解过程可以利用拉格朗日乘子法，即求目标函数

的最小值，来求出对应的最优解。为了求解方便，不妨假设

为正定矩阵，以保证其一定有逆矩阵，于是， 对

进行偏微分，有

相应三个偏微分等式，可以求得

对应

和

的偏微分，可以求得

方便起见，记

, 就有

和

将

带入目标函数，可以得到最小化的收益方差

可以看出，

可以表示为二次型形式，即

标准差与期望收益构成了一条曲线, 称之为 均值-方差前沿. 当以收益标准层

为横轴， 期望收益

为纵轴时，均值-方差曲线是一条双曲线的右支，是固定预期收益，与之对应的最小标准差的点集；如果以方差作为横轴，曲线则为一条抛物线，曲线上存在一点表示 所有组合中最小收益方差的组合，即全局最小方差投资组合。

有效前沿可视化 (代码警告)

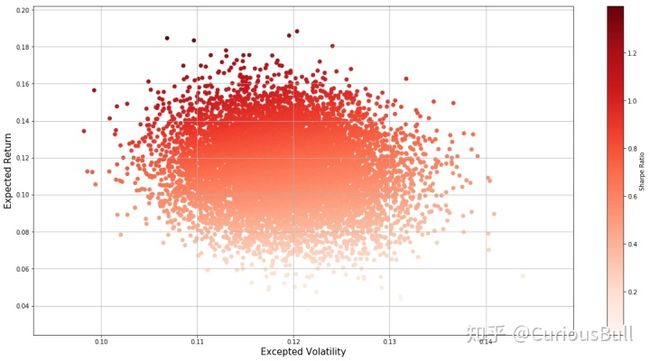
面对完枯燥的数学公式后，有必要有代码去对公式进行一次复习与可视化，笔者这里利用 Monte-Carlo 模拟的方 式，随机对沪深 300 的成分股从 2014 年到 2017 年的收益率进行一个简单的资产配置组合，并画出不同组合之 下的标准差 - 收益率散点图。

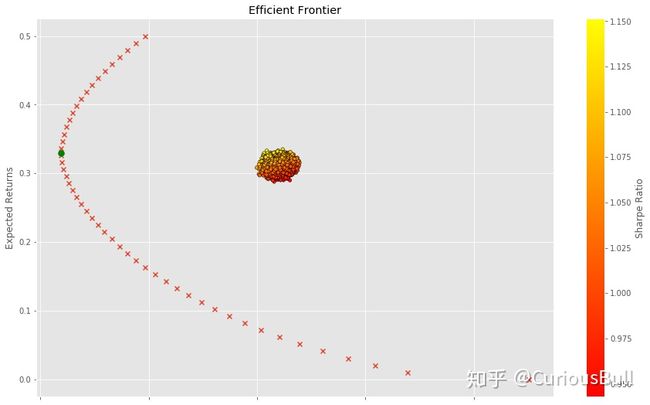
利用 Scipy.optimize 模块，可以求解在指定约束下，线性方程的最优解，笔者随后设置了固定收益率,并求解 出了不同收益率下，标准差最小值序列，由此画出了有效前沿。在散点图中，笔者标记了绿点为最小方差组合。

考虑到很多读者对于开源数据的使用不太熟练，笔者这里尽量详细地对代码实现进行逐步分解。

数据准备与预处理

1. 量价主要采用 QUANTAXIS 的数据，其采集了通达信的历史所有数据，并利用万得的复权计算公式可以重新对股票数据进行复权, 保存在本地数据库的数据，研究和使用无疑是最便利的。
2. 简单起见，笔者考虑的股票代码仅为当期沪深 300 的成分股，并利用聚宽的本地数据源获取了当期沪深 300 的成分股。
3. 对于交易日期处理，笔者这里用了一点小 trick, 利用 QUANTAXIS 本地维护的交易日期列表，笔者去获取了想要考察的时间段内真实交易日期
4. 笔者随机模拟了 50000 组资产组合，组合中的股票权重利用 np.random 实现随机分配
5. 对于收益率的计算，笔者同样使用了一点小 trick, 首先是建立对于 close 的透视表，然后基于透视表计算日收益率；然后是为了避免出现某些股票停牌日期太多，笔者对缺失值默认取 0.， 但是如果缺失值太多，数据量不到交易日期的 90%, 则相应丢弃该标的

import jqdatasdk
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.optimize import minimize

import QUANTAXIS as QA
from QUANTAXIS.QAUtil.QADate_trade import trade_date_sse  # 导入历史交易日列表，方便处理

jqdatasdk.auth("聚宽账户", "聚宽密码")


# 随机种子
np.random.seed(1001)


# 设置数据起始点和终结点
start = "2014-01-01"
real_start = QA.QAUtil.QADate_trade.QA_util_get_real_date(start, towards=1)
pre_start = trade_date_sse[trade_date_sse.index(real_start) - 1]  # 收益率计算时，往前多取一个交易日
end = "2017-12-31"
real_end = QA.QAUtil.QADate_trade.QA_util_get_real_date(end, towards=-1)

# 资产组合的数目
num_portfolios = 50000

# 导入沪深 300 股票
code_list = sorted(
    list(map(lambda x: x[:6], jqdatasdk.get_index_stocks("000300.XSHG")))
)

# 获取全市场股票定点前复权的收盘价
closes = (
    QA.QA_fetch_stock_day_adv(code=code_list, start=pre_start, end=real_end)
    .to_qfq()
    .pivot("close")
)


# 收益率与波动率计算
daily_return = closes.pct_change().drop(closes.index[0])
# 对于某些有停牌或者没上市股票，进行特殊处理
daily_return = daily_return.apply(
    lambda x: x.fillna(0) if len(x.loc[~pd.isna(x)]) > len(x) * 0.9 else np.nan
).dropna(axis=1)
annual_return = daily_return.mean() * 250.0

final_code_list = daily_return.columns.tolist()

不同资产组合的年化收益率、风险与夏普率计算

1. 组合的收益率与波动率计算可以对照如下公式

2. 将所有模拟的组合权重，收益率，风险等记录下来，方便之后寻找最佳收益率组合的权重

3. 模拟资产组合的收益风险基于夏普率的散点热度图如下所示：

# 组合收益
port_return = []
# 组合波动
port_volatility = []
# 夏普率
sharpe_ratio = []
# 组合中股票权重
stock_weights = []


def get_return_risk_sharpe(weights, risk_free=0.04):  # 假设年化无风险利率为 4%
    # 计算收益率
    returns = np.dot(weights, annual_return)  # r_p = sum(w_i*r_p)
    # 计算波动率
    volatility = np.sqrt(
        np.dot(weights.T, np.dot(annual_cov, weights))
    )  # sigma_P = w^TVw
    # 计算夏普比率
    sr = (returns - risk_free) / volatility
    return returns, volatility, sr


# 对所有资产组合进行随机权重分配，计算预期收益、波动率和夏普率
for port in range(num_portfolios):
    weights = np.random.random(len(final_code_list))
    weights /= np.sum(weights)
    returns, volatility, sr = get_return_risk_sharpe(weights)
    sharpe_ratio.append(sr)
    port_return.append(returns)
    port_volatility.append(volatility)
    stock_weights.append(weights)

portfolio = {
      
    "Returns": port_return,
    "Volatility": port_volatility,
    "Sharpe Ratio": sharpe_ratio,
}

# 将预期收益、波动率和夏普率以及个股权重拼接为 DataFrame
for counter, symbol in enumerate(final_code_list):
    portfolio[symbol + " Weight"] = [weight[counter] for weight in stock_weights]

df = pd.DataFrame(portfolio)
column_order = ["Returns", "Volatility", "Sharpe Ratio"] + [
    stock + " Weight" for stock in final_code_list
]
df = df[column_order]

# 可视化，观察均值-方差曲线的关于夏普率的热度图
plt.style.use("ggplot")
df.plot.scatter(
    x="Volatility",
    y="Returns",
    c="Sharpe Ratio",
    cmap="autumn",
    edgecolors="black",
    figsize=(15, 9),
    grid=True,
)
plt.xlabel("Volatility (Std. Deviation)")
plt.ylabel("Expected Returns")
plt.title("Efficient Frontier")
plt.show()

利用 Scipy.optimize 计算并画出有效前沿

# 可视化，计算有效前沿
# 定义优化目标函数 (固定收益率)
# 最小化风险函数
def min_std(weights):
    return get_return_risk_sharpe(weights)[1]


# 约束条件
constraints = {"type": "eq", "fun": lambda x: np.sum(x) - 1}  # 组合中资产权重之和为 1

# 将参数值(权重)限制在0.001和1之间,保证前沿上的点包含了所有资产
bins = tuple((0.001, 1.0) for x in range(len(final_code_list)))

# 权重初始值设置为均为分布, 最优化方法采用 Sequential Least-Squares Quadratic Programming (SLSQP)
min_risk = minimize(
    min_std,
    len(final_code_list) * [1.0 / len(final_code_list)],
    method="SLSQP",
    bounds=bins,
    constraints=constraints,
)

# 计算有效前沿上的投资组合
def get_efficient_frontier():
    stock_num = len(final_code_list)
    frontier_returns_array = np.linspace(0.0, 0.5, 50)  # 预期收益率序列
    frontier_sigma_array = []

    # 遍历每个收益率，去寻找风险最小的投资组合
    for ret in frontier_returns_array:
        # 约束条件：1.收益率等于ret；2.各权重和等于1
        frontier_cons = (
            {"type": "eq", "fun": lambda x: get_return_risk_sharpe(x)[0] - ret},
            {"type": "eq", "fun": lambda x: np.sum(x) - 1},
        )
        frontier_point = minimize(
            min_std,
            stock_num * [1.0 / stock_num],
            method="SLSQP",
            bounds=bins,
            constraints=frontier_cons,
        )
        # print(frontier_point['x'])
        frontier_sigma_array.append(frontier_point["fun"])

    frontier_sigma_array = np.array(frontier_sigma_array)
    return frontier_returns_array, frontier_sigma_array


frontier_return, frontier_sigma = get_efficient_frontier()
# 绘制图形
plt.figure(figsize=(20, 10))
plt.style.use("ggplot")
df.plot.scatter(
    x="Volatility",
    y="Returns",
    c="Sharpe Ratio",
    cmap="autumn",
    edgecolors="black",
    figsize=(15, 9),
    grid=True,
)
plt.xlabel("Volatility (Std. Deviation)")
plt.ylabel("Expected Returns")
plt.title("Efficient Frontier")

# 绿点代表最小方差组合
min_sigma_point, = plt.plot(
    get_return_risk_sharpe(min_risk["x"])[1],
    get_return_risk_sharpe(min_risk["x"])[0],
    "g.",
    markersize=15.0,
)

# 叉号代表有效前沿
plt.scatter(frontier_sigma, frontier_return, marker="x")
plt.show()

思考

很神奇，实际上，不同组合的收益-方差散点图应该与有效前沿贴合的，但是却离有效前沿一大段，具体原因读者们可以去看参考 [7]. 大体而言，A 股的收益率变化实在太大，牛短熊长，2018 年甚至一整年都没有正收益，这样的市场，也难关普通的长周期基本面量化策略会折戟沉沙了。

读者们如果感兴趣，MPT 在建立合理的投资标的组合会有比较好的作用。

结语

本来打算在一篇文章中对 MPT，CAPM，APT 进行彻底地整理与讲述，但是实际整理起来，发现内容远比自己预想的要多，只能在下一篇中，补充上 CAPM， APT 相关内容了。

Footnotes

[^1]: 半正定矩阵定义为，对于任意一个非零向量

, 矩阵

满足

. 同理，正定矩阵满足

.

参考

[1]:《主动投资组合管理》 -- [美]格林诺德 (Grinold, R.C), [美]卡恩 (Kahn, R.N.)

[2]: 《量化股票组合管理》 -- [美]路德维希 B. 钦塞瑞尼（Ludwig B. Chincarini） 金大焕（Daehwan Kim）

[3]: Modern portfolio theory

[4]: MPT 模型

[5]: 基于JQData及Monte Carlo模拟来建立有效前沿组合，并找出最优组合和有着最低波动率的组合

[6]: [Python绘制上证50成分股有效前沿和CML](曲曲菜：【投资组合理论】Python绘制上证50成分股有效前沿和CML)

[7]: [有效前沿与模拟投资组合分离的原因](曲曲菜：【投资组合理论】有效前沿与模拟投资组合分离的原因)