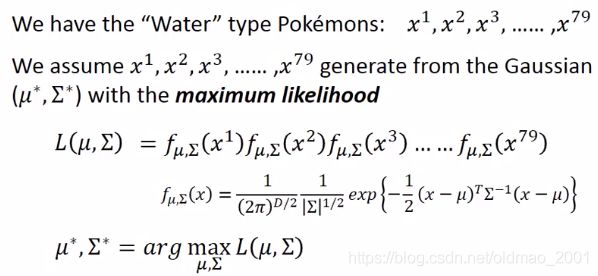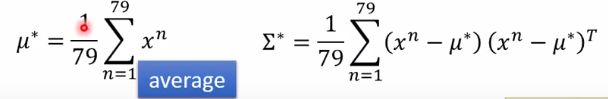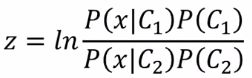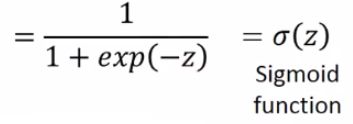李宏毅 2020 Machine Learning:Classification
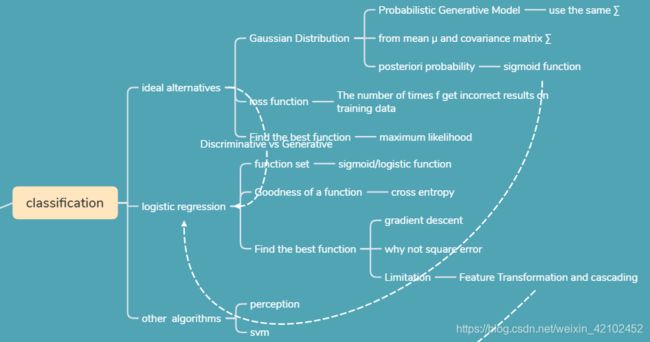
思维导图
先导知识
监督学习的任务就是学习一个模型(或者得到一个目标函数),应用这一模型,对给定的输入预测相应的输出。这一模型的一般形式为一个决策函数Y=f(X),或者条件概率分布P(Y|X),属于统计学模型。 监督学习方法又可以分为生成方法和判别方法,所对应的模型分别为生成模型(generative model)和判别模型(discriminative model),在概率图上建立,属于贝叶斯角度。概率图分为有向图(bayesian network)与无向图(markov random filed)。有向图多为生成模型,无向图多为判别模型。
决策函数和条件概率分布
决策函数Y=f(X):输入X,输出Y,Y与阈值比较,根据比较结果判定X属于哪个类别。
条件概率分布P(Y|X):输入X,通过比较它属于所有类的概率,将输出概率最大的类作为该X对应的类别。例如:如果P(w1|X)大于P(w2|X),那么我们就认为X是属于w1类的。
两个模型都可以实现对给定的输入X预测相应的输出Y的功能。实际上通过条件概率分布P(Y|X)进行预测也是隐含着表达成决策函数Y=f(X)的形式的。 而同样,很神奇的一件事是,实际上决策函数Y=f(X)也是隐含着使用P(Y|X)的。因为一般决策函数Y=f(X)是通过学习算法使你的预测和训练数据之间的误差平方最小化,而贝叶斯告诉我们,虽然它没有显式的运用贝叶斯或者以某种形式计算概率,但它实际上也是在隐含的输出极大似然假设(MAP假设)。也就是说学习器的任务是在所有假设模型有相等的先验概率条件下,输出极大似然假设。
判别方法和判别模型
判别模型:有限样本==》判别函数 = 预测模型==》预测
判别方法由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型,即判别模型。判别方法关心的是对给定的输入X,应该预测什么样的输出Y。
判别模型(Discriminative Model),又可以称为条件模型,或条件概率模型。估计的是条件概率分布(conditional distribution),p(class|context)。利用正负例和分类标签,主要关心判别模型的边缘分布。其目标函数直接对应于分类准确率。
主要特点:寻找不同类别之间的最优分类面,反映的是异类数据之间的差异。
优点:(1)分类边界更灵活,比使用纯概率方法或生产模型得到的更高级;(2)能清晰的分辨出多类或某一类与其他类之间的差异特征;(3)在聚类、视角变化、部分遮挡、尺度改变等方面效果较好;(4)适用于较多类别的识别;(5)判别模型的性能比生成模型要简单,比较容易学习。
缺点:(1)不能反映训练数据本身的特性,即能力有限,可以告诉你的是1还是2,但没有办法把整个场景描述出来;(2)缺少生成模型的优点,即先验结构的不确定性;(3)黑盒操作,即变量间的关系不清楚,不可视。
常见的有:logistic regression、SVMs、traditional neural networks、Nearest neighbor、Conditional random fields。
主要应用:Image and document classification、Biosequence analysis、Time series prediction。
生成方法和生成模型
生成模型:无穷样本==》概率密度模型 = 产生模型==》预测
生成方法由数据学习联合概率分布P(X,Y),然后求出条件概率分布P(Y|X)=P(X,Y)/P(X)作为预测的模型。这样的方法之所以成为生成方法,是因为模型表示了给定输入X产生输出Y的生成关系。用于随机生成的观察值建模,特别是在给定某些隐藏参数情况下。
生成模型(Generative Model),又叫产生式模型。估计的是联合概率分布(joint probability distribution),p(class, context)=p(class|context)*p(context)。用于随机生成的观察值建模,特别是在给定某些隐藏参数情况下。在机器学习中,或用于直接对数据建模(用概率密度函数对观察到的样本数据建模),或作为生成条件概率密度函数的中间步骤。通过使用贝叶斯规则可以从生成模型中得到条件分布。如果观察到的数据是完全由生成模型所生成的,那么就可以拟合生成模型的参数,从而仅可能的增加数据相似度。但数据很少能由生成模型完全得到,所以比较准确的方式是直接对条件密度函数建模,即使用分类或回归分析。与描述模型的不同是,描述模型中所有变量都是直接测量得到。
【注:先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现.
后验概率是指依据得到"结果"信息所计算出的最有可能是那种事件发生,如贝叶斯公式中的,是"执果寻因"问题中的"因".】
所以生成模型和判别模型的主要区别在于:添加了先验概率。即:
生成模型:p(class, context)=p(class|context)*p(context)
判别模型: p(class|context)
主要特点:(1)一般主要是对后验概率建模,从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度;(2)只关注自己的类本身(即点左下角区域内的概率),不关心到底决策边界在哪。
优点:(1)实际上带的信息要比判别模型丰富;(2)研究单类问题比判别模型灵活性强;(3)模型可以通过增量学习得到;(4)能用于数据不完整(missing data)情况;(5)很容易将先验知识考虑进去。
缺点:(1)容易会产生错误分类;(2)学习和计算过程比较复杂。
常见的有:Gaussians、Naive Bayes、Mixtures of multinomials、Mixtures of Gaussians、Mixtures of experts、HMMs、Sigmoidal belief networks、Bayesian networks、Markov random fields。
主要应用:(1)传统基于规则的或布尔逻辑系统正被统计方法所代替;(2)医学诊断。
过去的报告认为判别模型在分类问题上比生成表现更加好(比如Logistic Regression与Naive Bayesian的比较,再比如HMM与Linear Chain CRF的比较)。当然,生成模型的图模型也有一些难以代替的地方,比如更容易结合无标注数据做semi-or-unsupervised learning。
作者:JasonDing
链接:https://www.jianshu.com/p/d195b887a32e
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
classification(分类问题)
分类问题的解决步骤与回归类似。
首先根据不同的特征将所有的输入数字化,然后假设一种最普遍的情况:这是一个二分类问题,那么我们可以简单地把它设为一个决策函数,g(x)>0时为一类,否则为另一类。损失函数相较来说好理解一些,在任何情况下都可以写成是判断分类是否正确的结果,如不正确则+1。在求最佳函数时,由于这个函数是无法微分的。学过的梯度下降无法解决这个问题,这次使用概率来解决。
高斯分布(正态分布)
Input:vector X;output:probability of sampling X.
The shape of the function determines by mean μ and covariance matrix ∑.
Assume the points are sampled from a Gaussian distribution. Find the Gaussian distribution behind them. Compute probability for new points. 新样本点距离高斯分布中心越远,概率越小,反之概率越大。
李航的《统计学习方法》中提到了最大熵模型,就是在逻辑回归那一章。基于最大熵情况下,高斯分布是最合适的分布。如表情包所示,万事不决用高斯。
1. 计算性质好
2. 在已知均值和方差的情况下高斯分布的熵是所有分布中最大的,数据分布未知时通常选择熵最大的模型
3. 现实中的很多随机变量是由大量相互独立的随机因素的综合影响所形成的,而其中每一个别因素在总的影响中所起的作用都是微小的,这种随机变量往往近似服从高斯分布(中心极限定理的客观背景)
作者:举头望明月 链接:https://www.zhihu.com/question/287631395/answer/460718073 来源:知乎 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
几率模型简单,参数比较少,偏差bias大,方差variance小,复杂的模型反之。如果特征向量中每一个特征都是独立的话,则每个特征都对应的一维高斯分布,这样训练出来的结果很差。因此,考虑特征之间的相互关系是很有必要的。
For binary features, you may assume they are from Bernoulli distributions.
If you assume all the dimensions are independent, then you are using Naive Bayes Classifier.
最大似然
样本可以从不同均值和协方差矩阵的高斯分布中sample出来,但是这些点的似然性不一样。我们可以计算不同高斯分布对样本的likelihood,然后取最大值,就找到了最大似然高斯分布。
求最小值就是求导后取极值,得到结果如下:
但是效果较差!
Probabilistic Generative Model的改进
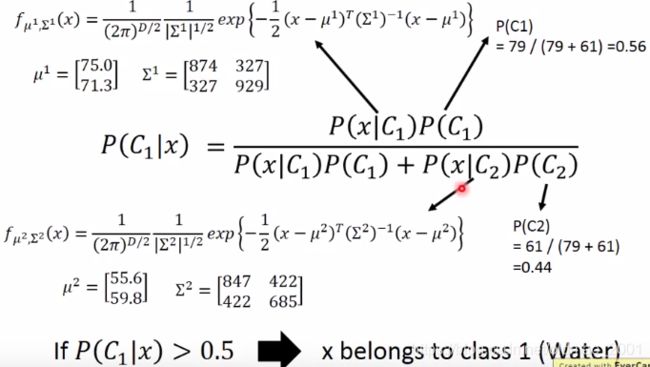
不同的分类使用相同的协方差矩阵∑,这样可以使得模型参数减少,防止过拟合。联立μ1,μ2,∑,构成 L(μ1,μ2,∑),求各自类别的样本的均值以及统一的∑。
后验概率(选学)
通过后验概率推出了sigmoid函数,为逻辑回归打下基础。
后续关于sigmoid的具体推导,可以跟着视频进行手推。
逻辑回归
![]()
function set
在上一节的基础上,我们直接在逻辑回归中使用sigmoid function。
![]()
Sigmoid函数也叫Logistic函数,是一个在生物学中常见的S型函数,也称为S型生长曲线。在信息科学中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的激活函数,将变量映射到0,1之间。它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。
Sigmoid作为激活函数有以下优缺点:
优点:平滑、易于求导。
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
Goodness of a function
![]()
即两个伯努利分布的交叉熵。
![]()
cross entropy,即两个分布接近的程度。如果两个分布一模一样,则H(p,q)=0,也就是说我们把function的输出以及target看成两个伯努利分布,我们希望这两个分布越接近越好,越接近则他们二者的交叉熵也就越小,目标就是要最小化cross entropy。
在信息论中,交叉熵是表示两个概率分布p,q,其中p表示真实分布,q表示非真实分布,在相同的一组事件中,其中,用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中,我们很难理解交叉熵的定义。下面举个例子来描述一下:
假设现在有一个样本集中两个概率分布p,q,其中p为真实分布,q为非真实分布。假如,按照真实分布p来衡量识别一个样本所需要的编码长度的期望为:
但是,如果采用错误的分布q来表示来自真实分布p的平均编码长度,则应该是:
H(p,q)=![]()
此时就将H(p,q)称之为交叉熵。交叉熵的计算方式如下:
对于离散变量采用以下的方式计算:H(p,q)=![]()
对于连续变量采用以下的方式计算:![]()
交叉熵可在神经网络中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
find the best function
依旧使用梯度下降法。
![]()
由于它是一个复合函数,所以它对wi求偏导可以使用链式法则:
![]()
![]()
![]()
为什么不用square error?
使用square error来做二分类在编程上或者说理论上没有问题,但是没有交叉熵来的顺。
1、离中心点很远的地方,它的Loss也为0,意味着它的参数update速度很慢,实际程序运行就好像卡住一样,反观交叉熵,离中心点越远,他的偏导值越大,更新参数步伐也就越大。
2、可以把learning rate设置大一点,以解决梯度参数update过慢的问题,但是这样也会有问题,如果初始点就在中心点附近,这个时候过大的learning rate可能over shooting。
Discriminative vs Generative
Generative model:假设数据来自高斯分布。脑补这个事情通常不好,因为数据没有明确告诉我们这个设定,但如果数据比较少,脑补会比较有用,就是你得到的情报很少,脑补可以让你得到更多的情报。朴素贝叶斯不考虑不同dimension之间的correlation,这两个dimension是独立产生的。
Discriminative model:没有假设,基于数据本身。
Benefit of generative model
●With the assumption of probability distribution, less training data is needed
Generative会遵循自己的假设,有时候甚至会忽略数据,所以在数据量小的时候比较有优势,Discriminative 则靠数据说话,随着数据量增大,Discriminative 模型的error应该是越来越小。
●With the assumption of probability distribution, more robust to the noise
当数据所含noise比较多,Generative要比Discriminative 模型要好,因为数据的label有问题,Generative做了脑补会把数据中的noise问题忽视掉。
●Priors and class-dependent probabilities can be estimated from different sources
Generative更便于联系不同类别但相互关联的数据。
Multi-class Classification(选学)
Limitation of Logistic Regression
有些情况下,无论我们选择什么参数,分界线都不可能把不同类的点完全分开。
1、Feature Transformation(纯粹的特征转换不实用,失去了机器学习的意义)
2、Cascading
这是深度学习最基本的模型。