通过Python实现K-means算法

K-means算法

K-means是机器学习中很常用的聚类算法, 关于K-means算法的数学原理, 算法, 伪代码等已经有非常丰富的文献资料, 这里就不介绍了. 直接看代码.

• 调用以下库

import numpy as np   #用于抽样和生成随机数
from sklearn.cluster import KMeans   #sklearn自带的Kmeans算法, 用于严重本文算法结果是否正确
import matplotlib.pyplot as plt     #结果可视化
import sys   #需要用到sys.exit()函数

如果你不需要验证聚类结果可以不使用Sklearn库

• 生成用于训练的随机数据

np.set_printoptions(suppress=True)    #令numpy的结果不以科学计数法的方式输出
Data = np.array([[1.0, 2.0], [1.5, 1.8], [3, 4], [6, 8], [8, 8], [1, 0.6],
                 [9, 11], [7, 10]])  #你也可以通过抽样的方式来更快的获得测试数据

• 定义用于选择随机初始点和簇数(k)的函数

def K_means(data, k):
    global Mean
    mean = []
    a = np.max(data[:, 0])
    b = np.min(data[:, 0])
    c = np.max(data[:, 1])
    d = np.min(data[:, 1])
    for i in range(k):
        x = np.random.uniform(a, b, 1)  
        #此处返回array
        y = np.random.uniform(c, d, 1)  #此处返回array
        mean.append([float(x), float(y)])
    Mean = np.array(mean)
    return Mean

上方代码中为了限定初始点(x,y)的位置不过分远离样本点, 所以将均匀抽样的上下限定为了训练数据横纵坐标的最大最小区间(a,b)和(c,d).

• 定义可视化函数, 绘制测试数据散点图

def vision(data, cell):
    plt.figure(figsize=(12,6))
    ax1 = plt.subplot(121)
    ax1.scatter(Data[:, 0], Data[:, 1])   #原始数据散点图
    ax1.scatter(point[:, 0], point[:, 0])    #同时将随机选取的初始点表示出来
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("scatter of " + "rural" + " data")
    ax2 = plt.subplot(122)
    ax2.scatter(Data[:, 0], Data[:, 1])    #原始数据散点图
    ax2.scatter(data[:, 0], data[:, 1])     #经过迭代后最终确定的聚类点
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("scatter of " + cell + " data")
    plt.show()

将聚类结果可视化对判断聚类结果是否准确非常重要.

• 定义迭代过程, 通过不断计算各个样本对聚类点的欧式聚类, 来不断更新聚类点

def iteration(Data, point):
    A = []
    B = []
    for i in range(len(Data)):
        d1 = np.sqrt(sum(pow(Data[i] - point[0], 2)))
        d2 = np.sqrt(sum(pow(Data[i] - point[1], 2)))
        if d1 > d2:
            A.append(list(Data[i]))
        else:
            B.append(list(Data[i]))
    if len(A) == len(Data) or len(B) == len(Data):
        print("初始化错误")
        sys.exit(0)
    new_x1 = np.mean(np.array(A)[:, 0])
    new_y1 = np.mean(np.array(A)[:, 1])

    new_x2 = np.mean(np.array(B)[:, 0])
    new_y2 = np.mean(np.array(B)[:, 1])
    new_point = np.array([[new_x1, new_y1], [new_x2, new_y2]])
    return new_point

注意, 上段代码中加入了一个if语句

    if len(A) == len(Data) or len(B) == len(Data):
        print("初始化错误")
        sys.exit(0)

这个条件语句是非常必要的, 因为初始点是随机生成的, 那么就有可能会出现所有样本点都只靠近一个聚类中心而远离另外一个聚类中心, 这样就无法形成两个簇, 程序会报错, 所以我们需要剔除这种情况的发生. 一旦所有的样本点只靠近一个聚类中心时令程序停止.

• 执行迭代

def fit(Data, object, n=20, max_iter=300, eps=1e-5,plot=None):
    err = 0
    for i in range(n):
        res = iteration(Data, object)
    print(res)
    if plot == True:
        vision(res,cell="object")
    else:
        pass
    return res

如果不指定迭代次数那么将默认迭代20次, 但最大迭代次数不超过300次, plot=True时可视化聚类结果, 默认不进行可视化

• 完整代码如下

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import sys


np.set_printoptions(suppress=True)
Data = np.array([[1.0, 2.0], [1.5, 1.8], [3, 4], [6, 8], [8, 8], [1, 0.6],
                 [9, 11], [7, 10]])  #实验数据

def K_means(data, k):
    global Mean
    mean = []
    a = np.max(data[:, 0])
    b = np.min(data[:, 0])
    c = np.max(data[:, 1])
    d = np.min(data[:, 1])
    for i in range(k):
        x = np.random.uniform(a, b, 1)  
        #此处返回array
        y = np.random.uniform(c, d, 1)  #此处返回array
        mean.append([float(x), float(y)])
    Mean = np.array(mean)
    return Mean


def vision(data, cell):
    plt.figure(figsize=(12,6))
    ax1 = plt.subplot(121)
    ax1.scatter(Data[:, 0], Data[:, 1])
    ax1.scatter(point[:, 0], point[:, 0])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("scatter of " + "rural" + " data")

    
    ax2 = plt.subplot(122)
    ax2.scatter(Data[:, 0], Data[:, 1])
    ax2.scatter(data[:, 0], data[:, 1])    
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("scatter of " + cell + " data")
    plt.show()


def iteration(Data, point):
    A = []
    B = []
    for i in range(len(Data)):
        d1 = np.sqrt(sum(pow(Data[i] - point[0], 2)))
        d2 = np.sqrt(sum(pow(Data[i] - point[1], 2)))
        if d1 > d2:
            A.append(list(Data[i]))
        else:
            B.append(list(Data[i]))
    if len(A) == len(Data) or len(B) == len(Data):
        print("初始化错误")
        sys.exit(0)
    new_x1 = np.mean(np.array(A)[:, 0])
    new_y1 = np.mean(np.array(A)[:, 1])

    new_x2 = np.mean(np.array(B)[:, 0])
    new_y2 = np.mean(np.array(B)[:, 1])
    new_point = np.array([[new_x1, new_y1], [new_x2, new_y2]])
    return new_point


def fit(Data, object, n=20, max_iter=300, eps=1e-5,plot=None):
    err = 0
    for i in range(n):
        res = iteration(Data, object)
    print(res)
    if plot == True:
        vision(res,cell="object")
    else:
        pass
    return res


point = K_means(Data, 2)  
fit(Data=Data, object=point,plot=True)

从上述代码来看, 实际上Kmeans算法只有两个核心的过程: point = K_means(Data, 2) 生成初始点并给定簇数; 执行迭代fit(Data=Data, object=point,plot=True)

• 执行结果
  

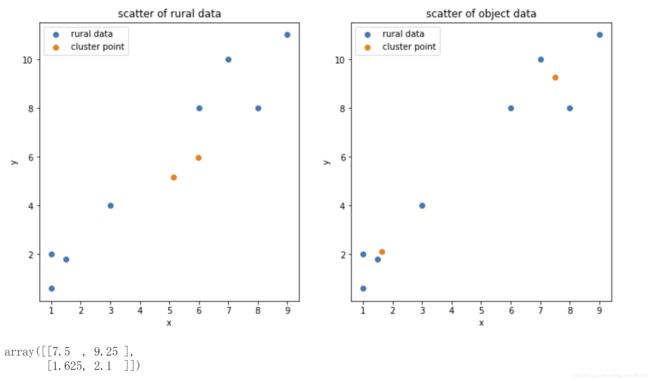
可以看到最终的聚类中心是(1.625, 2.1)和(7.5, 9.25), 那么这个结果是否正确呢？接下来将同样的数据集放入Sklearn.KMeans中运行

clf = KMeans(n_clusters=2)
clf.fit(Data)  # 分组
 
centers = clf.cluster_centers_ # 两组数据点的中心点
labels = clf.labels_   # 每个数据点所属分组
print(centers)

• Sklearn运行结果
  
  可以看到结果与本文代码保持一致. 但本文加入了聚类结果的可视化, 同时也能给出簇中包含了那些样本, 因为在迭代函数iteration(Data, point)中将它们存入了A和B两个列表中, 只需要return A, B就可以得到它们.

tips

K-means这种聚类算法需要给定初始点, 而聚类结果又非常依赖初始点的位置, 这就导致了上述代码多次运行时可能会得到不一样的结果, 这与Sklearn.KMeans的情况相同, 所以这并不是程序出现了前后不一的错误, 而是算法本身的局限性所导致的. 所以你应该多次运行聚类算法才能得到稳定的聚类中心. 关于K-means算法的详细解释可以参考Sklearn库给出的KMeans手册.