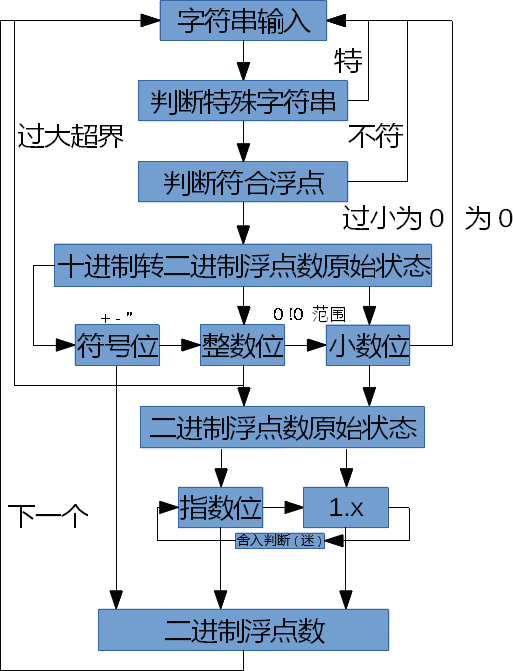
python - 接近完美的单精度浮点数转换代码

浮点数存储

十进制浮点数转换为二进制浮点数：整数部分重复相除，小数部分重复相乘
整数部分重复相除：除基取余，直到商为0，余数反转
小数部分重复相乘：乘基取整，直到小数为0或者达到指定精度位，整数顺序排列
匠心之作java基础强化之强转溢出&浮点数运算精讲

0.5
过程1：转换乘对应的二进制小数 0.1
过程2：转换成对应的指数形式 2**1 * 1.0

过程1分解，因为这里整数部分为0不用处理，相当于只需要了解怎么把十进制的.5变成二进制的.1，在人的思维中，这里的1就相当于2**-1，正好是0.5，但是这对计算机来说是没有意义的，计算机的运算器都是整数的运算，再观察，假设目标形态是x，0.5 * 2=1；x * 2=1，于是bin(0.1) is float(0.5)，那么如何用0.5推导出0.1，* 2对二进制意味着是比特左移，而小数点左边，对于计算机来说，是不认识小数的，于是只能当作整数处理，那么小数点左边这个整数就是5，5 * 2=10，即0.5 * 2=1，所以没假设的整数结果大于10后，就把这个十位拿掉存放起来，例如5 * 2一次就得到一个十位的1，拿掉1后就是0，获取小数结束：.1
那么为了知道规律，设定数值：bin(.11)即2**-1+2**-2即0.5+0.25即0.75

这里整数部分就是两位了，把这两个数当作整数就是75，那么要获取有效的1只能是百位：
75 * 2=150，拿掉百位的1，存储起来，待处理整数为50，50 * 2=100，拿掉百位的1，待处理数归零，取值结束，连续的获取了两个1，即bin(.11)
第一次拿掉的1，他表示的是0.5，第二次拿掉的1表示的是0.25，对应.11，第二次产生的1是放在第一次产生的1的后面。

假设我们不拿掉1，是否会有影响，150*2=300，个位、十位归零，运算结束，得到百位以上的数是3，3可以直接可以用二进制的数11表示，貌似也行。
方法1对应方法2的逻辑上的缺点：
1、貌似每次都要把超位的1都拿下来，这一步可以省去吗？
2、需要存储拿下来的1

优点：
1、超位后，拿掉一个位，之后就能少算一个位，于是每发生一次，之后运算压力都会减小，尤其是如果给一个小数点后很长数值的情况
2、接上，我们要每次都要推测超位的长度，因为我们规定了浮点数的数据存储长度就是那么多，存储长度盛满后，后面可能有的小数就要省略。而如果把位拿下来存在个东西里面，就只需要记录东西里面的长度。其实这里我很不确定，例如我用Python来表示，我会用到这个那个函数，但是我不知道机器中，是否有超位的部分的对应二进制的长度的运算方法。其实推测下来，可能的情况是待处理的数据其实是字符串，因为长度不定，计算机底层可能还无法存放那么长的数据，所以可能会需要用软件分割处理，所以不是单纯的数值，而数值只是计算的中间产物，而之后存放的二进制1，也是字符串，即：待处理字符串 == > 转换成运算器能处理的长度 == > 运算 == > 得到超位 == > 存放至表示二进制的字符串中。

上面提到的是小数部分如何转化成二进制小数部分，那么整数部分，其实就可以用十进制转二进制的方法直接转化成二进制整数部分。

Python 十进制转二进制

但是当作一个模拟硬件工作的流程，整数的0~9以及个十百千又如何变成二进制保存和运算的呢。保存其实就是一串二进制的01的串而已，没有类型规定的话，就是RAW。
又要开始思考了，假设我们拿到一个功能，即二进制1000就直接对应8，再底层的功能我们不考虑。
那么64位的cpu，他一次运算的长度可以是1111…挺长的，那就短说，假设我们用的处理器是4004，一次运算长度是4bit，即1111，从左往右，1分别对应8、4、2、1，最大表示无符号十进制15，假设给出整数0~9的任意一个，例如8，他记住了bin(1000)是8，结果就直接出来了。例如7，他至少知道7比8小，比4大，所以7-4=3，同理3-2=1，于是0111，当然他也可能直接记住7是0111。那么给出16呢，超出15的界限，这才开始真正的思考而不是推测+思考。16是一个字符串，他符合整数的书写规则，而且我们也是要把他当作整数处理。底层库中并没有他的数据，但是运算器中有3/2=1…1；5/2=2…1；6/2=3；7/2=3…1；9/2=4…1的数据，16就是一个十位的1和一个个位的6，16/2=（10+6）/2=5+3=8，而8正好是1000，而十进制的/2运算就是二进制的位移运算，所以16的二进制形态就是10000，那么17呢，17/2=（10+7）/2=8…1，余号前面意味着仍有10000，但余数意味着之前有个1，那么就是10000+1=10001。貌似有了苗头，只需要定义一个10/2=5。
那么一个更大点更复杂的数，例如bin(111111)，int(0b111111): 63。求63在4004下转成二进制形态的过程。
5/2=2…1 : 1 2/2=1…0 : 0 1/2=0…1 : 1 5:bin(101)

bin(1010):10 10/2=5…0 : 0 5 : 101 越开始的位，越是二进制的低位（右侧）

    s=str(i%2)+s
    i=i//2

>>>s '1010011000' ```缕一缕思路，只要整数/2，无论整除还是有余，得到的结果相对于二进制来说，都是上了一位。而余数就是当前位置二进制的单位。

无注释版：

import re

while 1:
    num = str(input("输入一个数，显示其浮点数在二进制中的存储，输入exit退出："))
    if num=="exit":
        print("退出运算")
        break
    if num=="0":
        print("00000000000000000000000000000000")
        continue
    if num=="nan":
        print("01111111110000000000000000000000")
        continue
    if num=="inf":
        print("01111111100000000000000000000000")
        continue
    if num=="-inf":
        print("11111111100000000000000000000000")
        continue

    if ((not re.compile("[^0-9.\-+]+").findall(num)) \
            and re.compile("[0-9]+").findall(num) \
            and ((num.count("-") == 0 and num.count("+") == 0) \
                 or (num.count("+") == 0 and num.count("-") == 1 and num[0] == "-") \
                 or (num.count("-") == 0 and num.count("+") == 1 and num[0] == "+")) \
            and (num.count(".") == 0 or num.count(".") == 1)):

        if num[0]=="-":
            sign="1"
            num=num[1:]
        elif num[0]=="+":
            sign="0"
            num = num[1:]
        else:sign="0"

        if num.count("."):
            numi=num[0:num.find(".")]
            numm=num[num.find(".")+1:]
        else:
            numi = num
            numm = "0"

        if numi=="0" and numm=="0":
            print("00000000000000000000000000000000")
            continue

        numib=bin(int(numi if numi else "0"))[2:]

        if numm!="0":
            nummb=""
            top=10**len(numm)
            numm=int(numm)
            if numib != "0":
                lmb=(25-len(numib))
                while len(nummb)<lmb:
                    numm=numm*2
                    if numm>top:
                        nummb+="1"
                        numm-=top
                    elif numm==top:
                        nummb += "1"
                        break
                    else:nummb += "0"
            else:
                for i in range(126):
                    numm = numm * 2
                    if numm<top:nummb += "0"
                    elif numm>top:
                        nummb += "1"
                        numm -= top
                        for i in range(24):
                            numm = numm * 2
                            if numm > top:
                                nummb += "1"
                                numm -= top
                            elif numm == top:
                                nummb += "1"
                                break
                            else:
                                nummb += "0"
                        break
                    elif numm==top:
                        nummb += "1"
                        break
            if "1" not in nummb:
                print("数值过小，赋值为0\n00000000000000000000000000000000")
                continue
        else:nummb="0"

        numb=numib+"."+nummb

        nume=numb.find(".")-1 if numb.find("1")<numb.find(".") else -(numb.find("1")-1)
        print(numb)
        if nume>127:
            print("数值过大，超出范围")
            continue
        exponent=bin(nume+127)[2:].rjust(8,"0")

        mantissa=numb[:numb.find(".")]+numb[numb.find(".")+1:]
        mantissa=mantissa.lstrip("0")
        print(bin(nume+127))

        if sign=="0" and len(mantissa)==25 and mantissa[24]=="1":
            mantissa=bin(int(mantissa[:25],2)+1)[2:]
            if len(mantissa)==26:
                exponent=bin(nume+127+1)[2:].rjust(8,"0")

        if len(mantissa)<25:print("该浮点数精确无舍入")
        else:print("该浮点数不精确有舍入")
        
        mantissa=mantissa[1:24].ljust(23,"0")
        numf=sign+exponent+mantissa
        print(numf)

    else:
        print("格式错误，无法转换为浮点数")

注释版：

import re

# 首先我们要知道在没有软硬件支持浮点数的那个时代，先贤们是怎么定义了单精度浮点数
# 并利用那时的条件运算出来。经过多次改良优化后，我攒出了以下代码
# 首先要了解单精度浮点数：32位的存储长度，其中第一位存储正负号：sign bit
# 接下来的八位存储指数：2**E，exponent，8位二进制范围是0~256，但因为之后
# 定义基数为1.x的原因，所以E要适应有效数字在小数点前咋滴咋滴，小数点后咋滴咋滴
# 所以将01111111，即127作为基准位0。所以E的有效范围是-127~128，但又因为在浮点系统中
# 定义了几个特殊的项，所以还是占用了几个E，大家可以用struct玩玩看
# 基数，1.x，在浮点数的二进制中，1会被隐去。.x的二进制占23位。python与IEEE754
# 在最后位除非被其舍去的下一位有分歧，python是0舍1入。IEEE754是直接截断。（可能）
# 所以我在代码中做了第25位的判断 /嘿嘿嘿 又优化了运算过程，并给出数值是否被舍入
while 1:
    num = str(input("输入一个数，显示其浮点数在二进制中的存储，输入exit退出："))
    if num=="exit":#此处几个if是float定义的几个量
        print("退出运算")
        break
    if num=="0":#此处几个if是float定义的几个量
        print("00000000000000000000000000000000")
        continue
    if num=="nan":#没有数
        print("01111111110000000000000000000000")
        continue
    if num=="inf":#无穷大
        print("01111111100000000000000000000000")
        continue
    if num=="-inf":#无穷小
        print("11111111100000000000000000000000")
        continue

    #检测字符串是否符合浮点数规格
    if ((not re.compile("[^0-9.\-+]+").findall(num)) \
            and re.compile("[0-9]+").findall(num) \
            and ((num.count("-") == 0 and num.count("+") == 0) \
                 or (num.count("+") == 0 and num.count("-") == 1 and num[0] == "-") \
                 or (num.count("-") == 0 and num.count("+") == 1 and num[0] == "+")) \
            and (num.count(".") == 0 or num.count(".") == 1)):

        #判断正负
        if num[0]=="-":
            sign="1"
            num=num[1:]
        elif num[0]=="+":
            sign="0"
            num = num[1:]
        else:sign="0"

        #分离整数部分和小数部分
        if num.count("."):
            numi=num[0:num.find(".")]
            numm=num[num.find(".")+1:]
        else:
            numi = num
            numm = "0"

        if numi=="0" and numm=="0":
            print("00000000000000000000000000000000")
            continue

        #整数部分的二进制
        # 虽然这里我用了bin直接转换整数为二进制，但是实际上
        # 那个年代使用的整数是多少位的，因为浮点数最大支持3.x * 10**38
        # 要远比int大的多
        numib=bin(int(numi if numi else "0"))[2:]

        #小数部分的二进制
        #如果numm不为0，进行运算，else，直接赋值nummb="0"
        if numm!="0":
            #存储二进制的字符串
            nummb=""
            #作为比较的基数，之后底数*2，二进制的意思就是向左位移1
            # 等一等，那我岂不是，冷静下，不是这样的，因为这里要算出
            # 对应的浮点数的小数点二进制部分，而此时根本不知道小数点
            # 二进制部分如何表示，这里就是要运算出来，而不是单纯的
            # 向左位移，而top这个就想到与二进制中的1的位置，而小数点
            # 后的二进制则是黑盒，现在就是要用*2，即黑盒中的现在不知
            # 但以后确实能存在的二进制浮点数给推出来
            top=10**len(numm)
            numm=int(numm)
            #如果整数部分存在数值，先贤们用32位定义为单精度浮点数
            # 经过指数运算后最终留给1.x的.x表示长度是23个二进制位
            #为了节省运算效率，不做多余的一丁点的运算，所以这里分叉了
            # 未优化前可是算152次的 127+25
            if numib != "0":
                lmb=(25-len(numib))
                while len(nummb)<lmb:
                    # *2相当于<<1
                    # 这里就是要把小数点后的二进制排列给挤出来
                    numm=numm*2
                    if numm>top:
                        nummb+="1"
                        numm-=top

                    #之前写过一个代码，有类似的过程，因为预先知道
                    # 之后不会有东西了，锁了舍去了num-的过程
                    # 直接跳出，但之后有用到num==0的判断，所以
                    # 这里激灵了一下，大概之后用不到numm了吧！？
                    elif numm==top:
                        nummb += "1"
                        break
                    else:nummb += "0"
            else:
                # 这个岔路，是整数部分为0的情况，所以1.x的位置很不确定
                # 所以就开始算，直到第一个有效数字出现，然后再算24个数字
                # 之前说过无脑152，但是这里简化以下，如果在e的最大值126下
                # 仍然无法得到有效数值，就直接赋值为0
                for i in range(126):
                    numm = numm * 2
                    if numm<top:nummb += "0"
                    elif numm>top:
                        nummb += "1"
                        numm -= top
                        for i in range(24):
                            numm = numm * 2
                            if numm > top:
                                nummb += "1"
                                numm -= top
                            elif numm == top:
                                nummb += "1"
                                break
                            else:
                                nummb += "0"
                        break
                    elif numm==top:
                        nummb += "1"
                        break
            # if nummb.find("1") == -1:
            # 文档说了，判断有没有用in，不用find
            if "1" not in nummb:
                print("数值过小，赋值为0\n00000000000000000000000000000000")
                continue
        else:nummb="0"

        #原始过程中的浮点数二进制不带正负号
        numb=numib+"."+nummb

        #原始二进制浮点转换成 1.x*(2**E) 计算2**E，指数
        nume=numb.find(".")-1 if numb.find("1")<numb.find(".") else -(numb.find("1")-1)
        print(numb)
        if nume>127:
            print("数值过大，超出范围")
            continue
        exponent=bin(nume+127)[2:].rjust(8,"0")

        #规整1.x
        mantissa=numb[:numb.find(".")]+numb[numb.find(".")+1:]
        mantissa=mantissa.lstrip("0")
        print(bin(nume+127))
        #判断是否需要入尾位，这个是python的特殊定义，IEEE 754 单精度浮点数转换并无舍入

        if sign=="0" and len(mantissa)==25 and mantissa[24]=="1":
            mantissa=bin(int(mantissa[:25],2)+1)[2:]
            if len(mantissa)==26:
                exponent=bin(nume+127+1)[2:].rjust(8,"0")

        if len(mantissa)<25:print("该浮点数精确无舍入")
        else:print("该浮点数不精确有舍入")
        #拼接浮点二进制
        mantissa=mantissa[1:24].ljust(23,"0")
        numf=sign+exponent+mantissa
        print(numf)

    else:
        print("格式错误，无法转换为浮点数")

以上是第三，不，第四天的码了，准确的说是从想写一个码开始，第五天了。这几天没什么学习进度，心里挺焦急的！

而实际上python默认并不会用到单精度浮点数，所以struct中的末位0舍1入到底是怎样，不的而知。
看看python实际上用的双精度浮点数吧！

In [87]: struct.unpack("!d",b'\x3f\xff\xff\xff\xff\xff\xff\xff')
Out[87]: (1.9999999999999998,)

In [90]: struct.pack("!d",1.9999999999999998)
Out[90]: b'?\xff\xff\xff\xff\xff\xff\xff'

In [91]: 2**-53
Out[91]: 1.1102230246251565e-16

In [92]: struct.pack("!d",1.99999999999999986)
Out[92]: b'?\xff\xff\xff\xff\xff\xff\xff'

In [93]: struct.pack("!d",1.99999999999999987)
Out[93]: b'?\xff\xff\xff\xff\xff\xff\xff'

In [94]: struct.pack("!d",1.99999999999999988)
Out[94]: b'?\xff\xff\xff\xff\xff\xff\xff'

In [95]: struct.pack("!d",1.99999999999999989)
Out[95]: b'@\x00\x00\x00\x00\x00\x00\x00'

In [96]: struct.unpack("!d",b'@\x00\x00\x00\x00\x00\x00\x00')
Out[96]: (2.0,)

In [97]: a=1.99999999999999989

In [98]: a
Out[98]: 2.0

In [99]: a=1.99999999999999988

In [100]: a
Out[100]: 1.9999999999999998

我要放弃思考

=============================================================================

两天，没白费，期间搞出好多问题，现在接近于当初还没有浮点软硬件支持时，前辈大佬们的想法了吧！

第二版，参照了前辈的代码思路 \心痛.png

import re

while 1:
    num = str(input("输入一个数，显示其浮点数在二进制中的存储，输入exit退出："))
    if num=="exit":#此处几个if是float定义的几个量
        print("退出运算")
        break
    if num=="0":#此处几个if是float定义的几个量
        print("00000000000000000000000000000000")
        continue
    if num=="nan":#没有数
        print("01111111110000000000000000000000")
        continue
    if num=="inf":#无穷大
        print("01111111100000000000000000000000")
        continue
    if num=="-inf":#无穷小
        print("11111111100000000000000000000000")
        continue

    #检测字符串是否符合浮点数规格
    if ((not re.compile("[^0-9.\-+]+").findall(num)) \
            and re.compile("[0-9]+").findall(num) \
            and ((num.count("-") == 0 and num.count("+") == 0) \
                 or (num.count("+") == 0 and num.count("-") == 1 and num[0] == "-") \
                 or (num.count("-") == 0 and num.count("+") == 1 and num[0] == "+")) \
            and (num.count(".") == 0 or num.count(".") == 1)):

        #判断正负
        if num[0]=="-":
            sign="1"
            num=num[1:]
        else:sign="0"

        #分离整数部分和小数部分
        if num.count("."):
            numi=num[0:num.find(".")]
            numm=num[num.find(".")+1:]
        else:
            numi = num
            numm = "0"

        #整数部分的二进制
        numib=bin(int(numi if numi else "0"))[2:]

        #小数部分的二进制
        if numm:
            nummb=""
            top=10**len(numm)
            numm=int(numm)
            print(numm)
            while len(nummb)<152:
                numm=numm*2
                if numm>=top:
                    nummb+="1"
                    numm-=top
                else:nummb+="0"
        else:nummb="0"

        #原始过程中的浮点数二进制不带正负号
        numb=numib+"."+nummb

        #原始二进制浮点转换成 1.x*(2**E) 计算2**E，指数
        nume=numb.find(".")-1 if numb.find("1")<numb.find(".") else -(numb.find("1")-1)
        exponent=bin(nume+127)[2:].rjust(8,"0")

        #规整1.x
        mantissa=numb[:numb.find(".")]+numb[numb.find(".")+1:]
        mantissa=mantissa.lstrip("0")

        #判断是否需要入尾位，这个是python的特殊定义，IEEE 754 单精度浮点数转换并无舍入
        if sign=="0" and mantissa[25]=="1":
            mantissa=bin(int(mantissa[:25],2)+1)[2:]
            if len(mantissa)==26:
                exponent=bin(nume+127+1)[2:].rjust(8,"0")

        #拼接浮点二进制
        mantissa=mantissa[1:24].ljust(23,"0")
        numf=sign+exponent+mantissa
        print(numf)

    else:
        print("格式错误，无法转换为浮点数")

参考：Python实现十进制小数转IEEE754单精度浮点数转换
参考中的代码有一次bug，是因为引入了浮点运算，浮点运算的舍入和内部显示导致结果会出现偏差甚至错误。
我改进了下，以至于以上代码是纯整数运算，并添加了python的舍入机制。

之前搞的错误思路的代码，贴在下边，删除以前的错误文章！

python - 浮点数的存储结构 一笔笔教你怎么算

我犯了个错误，本想用一段代码表示浮点的转换存储，但是里面却不断的使用着与浮点相关的运算，如果这几一个实用的东西的话，她就是个死循环。
1、一开始赋值就转换成float，这导致之后接受的都是转换后的数据，大几率的错误性
例如，了解浮点存储的，再去想最大浮点值
0 11111110 11111111111111111111111
+ 2**127 *1.99999999…=3.402823669209385e+38
我就想到0.9999999999999…这个很边缘的值，他在浮点M值以外的位舍入后，就是1.0了，而float就是这样干的
在此之前我就针对进位做了个运算了，但用0.9999999999999…验证时，才注意到了最初我就犯了错误。
本想着再模拟486以前的没有浮点机制的时候去写个。思路很难，即便完成了指数的取值，小数部分的取值又要涉及到浮点运算。
而且浮点之所以这么存储，大概也是为了做浮点间的运算的方便，之后就是一个个很深的水了，于是虽然不想放弃的我，放弃这个问题，赶紧学下去才是关键吧！至于那个往上的在线运算器，会不会就是利用struct写的，毕竟就是一句话的事！即便也是用输入是字符串，解析成浮点存储结构，也不难，但如果真的没有利用一点浮点运算，大家能写出来吗？

IEEE 754 单精度浮点数转换
我嗅探了下网络，这个运算是联网的，网址所在地：美国俄勒冈波特兰 亚马逊云

不过我还是想尝试下至少一开始是字符输入接收为字符串的方法

=======================================================
这段代码并不完善，但大家可以先看看，完善的代码在后面。

第一版：用的是算数的思路，自己啃书，磕出来的代码，在纸上算的话，可以说是完美，但是在电脑上算，涉及到了好多那个时代不该出现的浮点运算，甚至最开始输入的字符串转化时，就是转化成了浮点数，最关键的是他可能会发生舍入导致结果不是我们输入的那个结果，所以虽然是一个纸上的完美思路。但是实际仅有教学价值了吧！

while 1:
    try:#如果输入转化失败，激发之后的except:break，结束程序
        num=float(input("请输入一个浮点数，非数结束："))
    except:break
    if num==0:#此处几个if是float定义的几个量
        print("00000000000000000000000000000000")
        continue
    if num=="nan":#没有数
        print("01111111110000000000000000000000")
        continue
    if num=="inf":#无穷大
        print("01111111100000000000000000000000")
        continue
    if num=="-inf":#无穷小
        print("11111111100000000000000000000000")
        continue

    # 判断符号位 S：sign bit
    sign= "0" if num>0 else "1" #简化后的代码
    # if num>0:sign="0"
    # else:sign="1"

    # 推算指数 E:exponent 指数
    # 将数累计计算直到1.x的格式，一切都是二进制运算
    e=0
    if num>=2:
        while num>=2:
            num/=2
            e+=1
    elif num<1:
        while num<1:
            num*=2
            e-=1
    #以上累计的e
    exponent=bin(e+127).replace("0b","").rjust(8,"0")

    # 推算尾数 M:mantissa 尾数、小数部分
    num-=1
    if num==0:
        print(sign+exponent+"00000000000000000000000")
        continue
    mantissalist=[]
    #这里我一开始是使用字符串的，但是最后一位判断的原因，
    # 字符串无法修改，所以做成了列表
    for i in range(1,24):
        b=2**-i
        if num>b:
            num-=b
            mantissalist.append("1")
        elif num==b:
            num -= b
            mantissalist.append("1")
            break
        elif num<b:
            mantissalist.append("0")
    # print(i,num==0) #debug时增加的输出

    # 判断是否计算到最后位还有余数，余数是否大于等于无法显示的那位
    # 如果是，舍入结果是可显示的最后一位是1，这里我无法断定如果等于
    # 的话会怎样因为根本无法把正好等于的那个数打进去，但八成就是这样
    if i==23 and mantissalist[22]=="0" and num>=2**-24:
        mantissalist[22]="1"
    mantissa=''.join(mantissalist).ljust(23,"0")
    print(sign+exponent+mantissa)

以上是用python模拟的float存储方式，大家可以对应系统自带的一个库算出的结果对照，但是那个库貌似也不是真实存储状态，反正差不多！
这个是调用struct模块，返回各种效果，数据准确，大概。就是这里，给出的结果是0舍1入，至于python实际，要不咱算算？

import struct
# def binary(num):
#     return ''.join(bin(ord(c)).replace('0b', '').rjust(8, '0') for c in struct.pack('!f', num))
# 上面注释掉的是源代码，总是报错
while 1:
    try:a=float(input("输入一个数，他会输出对应的浮点数结构，输入非数类退出："))
    except:break
    else:
        print(''.join(bin(h).replace('0b','').rjust(8,'0') for h in struct.pack('!f',a)))

# 这里是我在写模拟过程时，用的0.0456与最后一位何时0何时1调用的几个参数
# print(struct.pack('!f',0.04559999704360962))
# print(struct.unpack('!f',b'=\xcc\xcc\xcd'))
# print(struct.unpack('!f',b'=:\xc7\x11'))
# print(struct.unpack('!f',b'=:\xc7\x10'))

使用unpack得到：
01110101100011100010001 0.04560000076889992
01110101100011100010000 0.04559999704360962
最后一位1，0.00000000372529030
0.04560000263154507

In [21]: struct.pack("!f",0.0455999979749322)
Out[21]: b'=:\xc7\x10'

In [22]: struct.pack("!f",0.04560000263154507)
Out[22]: b'=:\xc7\x12'

In [23]: struct.pack("!f",0.04560000263154506)
Out[23]: b'=:\xc7\x11'

额，不行，这个舍入无视末位0还是1，只要进位，可能会一串上去
还需要改

==========================================
额，暂时算法上搞定了，但是突然觉得这里从字符串该过来的列表又没必要了，所以再简化成字符串吧！

while 1:
    try:#如果输入转化失败，激发之后的except:break，结束程序
        num=float(input("请输入一个浮点数，非数结束："))
    except:break
    if num==0:#此处几个if是float定义的几个量
        print("00000000000000000000000000000000")
        continue
    if num=="nan":#没有数
        print("01111111110000000000000000000000")
        continue
    if num=="inf":#无穷大
        print("01111111100000000000000000000000")
        continue
    if num=="-inf":#无穷小
        print("11111111100000000000000000000000")
        continue

    # 判断符号位 S：sign bit
    sign= "0" if num>0 else "1" #简化后的代码
    # if num>0:sign="0"
    # else:sign="1"

    # 推算指数 E:exponent 指数
    # 将数累计计算直到1.x的格式，一切都是二进制运算
    e=0
    if num>=2:
        while num>=2:
            num/=2
            e+=1
    elif num<1:
        while num<1:
            num*=2
            e-=1
    #以上累计的e
    exponent=bin(e+127).replace("0b","").rjust(8,"0")

    # 推算尾数 M:mantissa 尾数、小数部分
    num-=1
    if num==0:
        print(sign+exponent+"00000000000000000000000")
        continue
    mantissalist=[]
    #这里我一开始是使用字符串的，但是最后一位判断的原因，
    # 字符串无法修改，所以做成了列表
    for i in range(1,24):
        b=2**-i
        if num>b:
            num-=b
            mantissalist.append("1")
        elif num==b:
            num -= b
            mantissalist.append("1")
            break
        elif num<b:
            mantissalist.append("0")
    # print(i,num==0) #debug时增加的输出

    # 判断是否计算到最后位还有余数，余数是否大于等于无法显示的那位
    # 如果是，舍入结果是可显示的最后一位是1，这里我无法断定如果等于
    # 的话会怎样因为根本无法把正好等于的那个数打进去，但八成就是这样
    if i==23 and num>=2**-24:
        # exec("mantissa=(bin(int(%s)+1).replace('0b','').rjust(23,'0')[-1:-24:-1][::-1])"%('0b'+''.join(mantissalist)))
        mantissa=(bin(int('0b'+''.join(mantissalist),2)+1).replace('0b','').rjust(23,'0')[-1:-24:-1][::-1])
    else:mantissa=''.join(mantissalist).ljust(23,"0")
    print(sign+exponent+mantissa)

还是有毛病，致命的大毛病，我获取的num本身其实就是个float，所以我不能使用a=float(input())。
而是要用a=str()，然后判断他是否符合录入对像的规则。

因为我录入0.9999999999999999999999，模拟她肯定接近于1，所以她的存储和1是一样的，于是struct是的，但是我的也是的，但我的不该是呀！所以错了！

请输入一个浮点数，非数结束：0.0456
0.0456
 01111010
00111101001110101100011100010001
请输入一个浮点数，非数结束：0.99999999999999999999999999999999
1.0
 01111111
00111111100000000000000000000000

于是我又加了个print，果然如此，所以继续改！亏的看了，不然真就错了！看来我注定不是一个码农，而是一个自由者！