查找-顺序+折半+索引+哈希【数据结构与算法】
大三党,大数据专业,正在为面试准备,欢迎学习交流。`文章中总结了四种常见的查找方法,内容包括了基本概念及代码实现。内容较多,特别是哈希查询的内容比较多。可能有所遗漏,但是总结了大部分的内容。
附带一本热销的电子书配套适用更佳,链接如下
大话数据结构
提取码:mazy往期文章
绪论-数据结构的基本概念
绪论-算法
线性表-顺序表和链式表概念及其代码实现
文章目录
- 1 常见的查找算法
- 2 平均查找长度ASL比较查找算法性能
- 3 顺序查找
-
- 3.1 顺序查找的思想
- 3.2 顺序查找代码
- 3.3 顺序表上顺序查找的平均查找长度(性能分析)
- 4 折半查找
-
- 4.1 折半查找的前提条件及查找过程
- 4.2 折半查找代码
- 4.3 折半查找的性能分析
- 4.4 折半查找特点
- 5 索引查找
-
- 5.1 索引的使用方法
- 5.2 索引表的构建
- 5.3 索引查找代码
- 5.4 索引顺序查找的ASL
- 6 三种查找算法的比较
- 7 哈希查找
-
- 7.1 哈希查询的思想
- 7.2 哈希函数的定义
- 7.3 哈希表的定义
- 7.4 常见的哈希函数
-
- 7.4.1 直接哈希函数
- 7.4.2 数字分析法
- 7.4.3 平方去中法
- 7.4.4 折叠法
- 7.4.5 除留余数法
- 7.4.6 随机数法
- 7.5 哈希函数选取通常需要考虑的因素
- 7.6 哈希函数冲突的处理方法
-
- 7.6.1 开放地址法
- 7.6.2 再哈希法
- 7.6.3 链地址法
- 7.6.4 公共溢出区法
- 7.7 哈希表查找代码实现及实例
- 7.8 哈希查找性能分析
- 总结
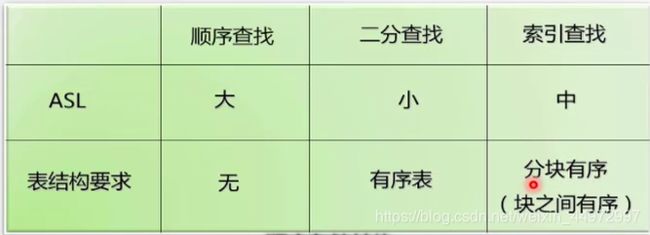
1 常见的查找算法
- 顺序查找
- 二分查找
- 索引查找
- 哈希查找
2 平均查找长度ASL比较查找算法性能
公式:ASL=P1C1+P2C2+…+PnC
Pi——查找第i个元素的概率
Ci——查找第i个元素需要的比较次数
3 顺序查找
3.1 顺序查找的思想
- 从表中指定位置(一般为最后一个,第0个位置设为岗哨)
的记录开始,沿某个方向将记录的关键字与给定值相比较,
若某个记录的关键字和给定值相等,则查找成功; - 反之,若找完整个顺序表,都没有与给定关键字值相等的
记录,则此顺序表中没有满足查找条件的记录,查找失败。
3.2 顺序查找代码
int seqsearch(DataType R[], KeyType key)
{
R[0]=key, i=n;//第一个位置设为岗哨
while (R[i] != key)
i=i-1;//从最后一个位置往前查找
return i;
}
3.3 顺序表上顺序查找的平均查找长度(性能分析)

对于顺序表的
Ci=n-i+1
Pi =1/n
则可以得到如下计算结果(等差数列的计算):
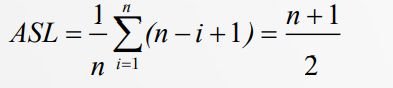
4 折半查找
4.1 折半查找的前提条件及查找过程
前提条件
如果顺序表中的纪律按关键字值有序即R[i].≤R[i+1],i=1,2,…,n-1,则称顺序表为有序表。

4.2 折半查找代码
int BinarySearch(DataType SL[], KeyType key, int n){
/*在长度为n的有序表SL中折半查找其关键字等于key的记录*/
/*查找成功返回其在有序表中的位置,查找失败否返回0*/
int low=1;
int high=n;
while(low<=high){
mid=(low+high)/2;//取整 小的数 右边的数
if(key = = SL[mid])
{
return mid;
}
else if( key>SL[mid])//查找值在左边 移动low
low=mid+1;
else //查找值在右边 移动low
high=mid-1;
}
return 0;
}
查找过程
将待查关键字与有序表中间位置的记录进行比较,若相等,查找成功,若小于,则只可能在有序表的前半部分,若大于则只可能在有序表的后半部分,因此,经过一次比较,就将查找范围缩小一半,这样一直进行下去直到找到所需记录或记录不在查找表中。
4.3 折半查找的性能分析
引入判定树
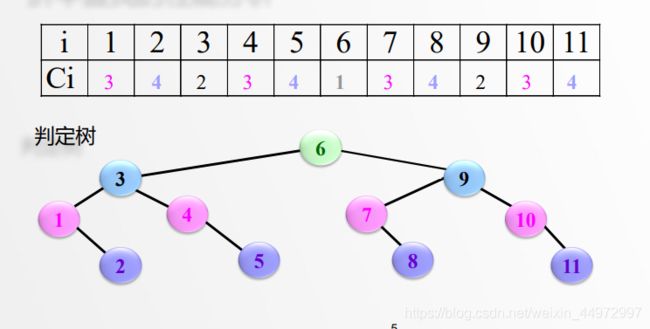
其中6查找一次。3 9查找两次。1 4 7 10 查找3次。2 5 8 11 查找4次。

4.4 折半查找特点
- 折半查找的查找效率高;
- 平均查找性能和最坏性能相当接近;
- 折半查找要求查找表为有序表;
- 并且,折半查找只适用于顺序存储结构
5 索引查找
5.1 索引的使用方法
- 先分析数据规律,建立索引
- 再根据索引进行快速定位
- 在定位的地方进行细致搜索
5.2 索引表的构建
- 分块:第Rk 块中所有关键字< Rk+1块中所有关键字,(k=1, 2, …, L-1)
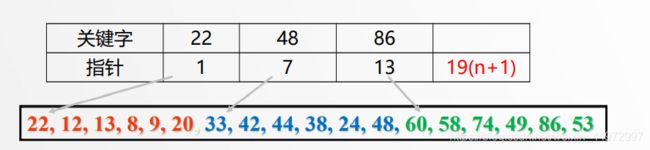
- 建立索引项:关键字项:记载该块中最大关键字值; 指针项: 记载该块第一个记录在表中位置。
- 建立索引表:所有索引项组成索引表
如下图展示
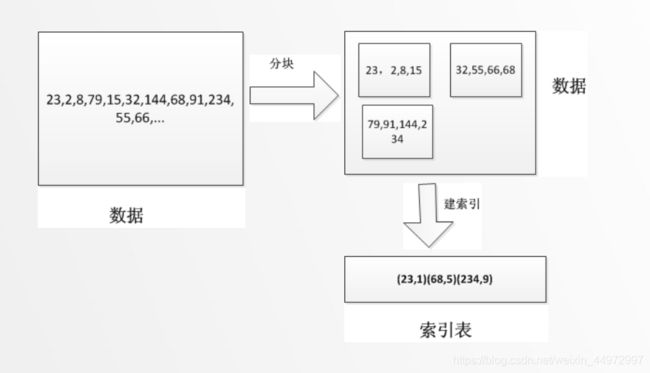
索引项展示
5.3 索引查找代码
typedef struct IndexType
{
KeyType key;//最大关键字
int Link; //地址项
} IndexType;
int IndexSequelSearch(IndexType ls[], DataType s[], int m, KeyType key){
/*索引表为ls[0]-ls[m-1],顺序表为s*/
i=0;
while(i<m && key>ls [i ].key) i++; /*块间查找*/
if(i==m)return -1; /*查找失败*//*不在查找范围内*/
else{
/*在块内顺序查找*/
j=ls[ i ].Link;
while(Key!=s[j].key && j<ls[ i+1 ].Link) //j<是为了不超出当前块
j++;
if(key = = s[j].key)return j; /*查找成功*/
else return -1; /*查找失败*/
}
}
5.4 索引顺序查找的ASL
6 三种查找算法的比较
7 哈希查找
7.1 哈希查询的思想
以学号查询为例子,取给定学号的后三位,不需要经过比较,便可直接从查找表中找到给定学生的记录。因为如下图我们建立了关键字和存储地址之间的映射关系。
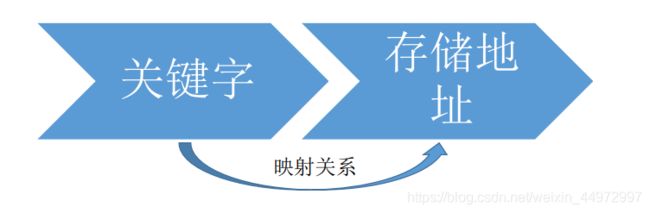
7.2 哈希函数的定义
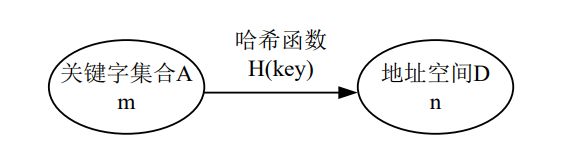
一般情况下,需在关键字与记录在表中的存储位置之间建立一个函数关系,以 H(key) 作为关键字为key 的记录在表中的位置,通常称这个函数 h(key) 为哈希函数。
-
哈希函数是一个映象,即:将关键字的集合映射
到某个地址集合上, 它的设置很灵活,只要这个地
址集合的大小不超出允许范围即可; -
由于哈希函数是一个压缩映象,因此,在一般
情况下,很容易产生“冲突”现象,即: key1!=
key2,而 h(key1) = h(key2)。例如下图 key分别是100和1000
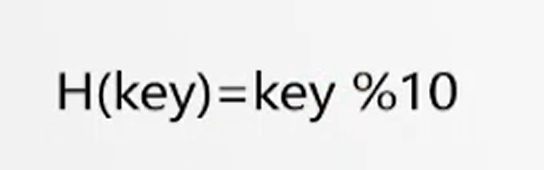
-
很难找到一个不产生冲突的哈希函数。一般情况
下,只能选择恰当的哈希函数,使冲突尽可能少地产
生。
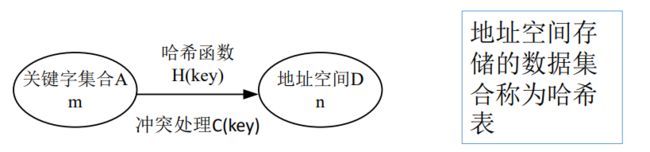
7.3 哈希表的定义
根据设定的哈希函数 H(key) 和提供的处理冲突的方法,将一组关键字映象到一个地址连续的地址空间上,并以关键字在地址空间中的“象”作为相应记录在表中的存储位置,如此构造所得的查找表称之为哈希表。
7.4 常见的哈希函数
7.4.1 直接哈希函数
7.4.2 数字分析法
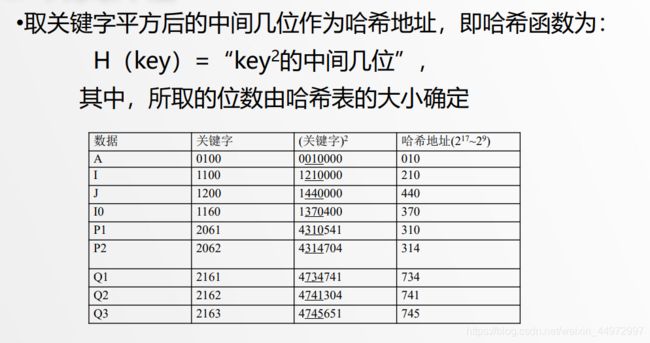
7.4.3 平方去中法
思想:以关键字的平方值的中间几位作为存储地址。求“关键字的平方值” 的目的是“扩大差别”和“贡献均衡”。
7.4.4 折叠法
7.4.5 除留余数法
7.4.6 随机数法
7.5 哈希函数选取通常需要考虑的因素
- 计算哈希函数所需时间;
- 关键字的长度;
- 哈希表的大小;
- 关键字的分布情况;
- 记录的查找频率。
7.6 哈希函数冲突的处理方法
7.6.1 开放地址法
为产生冲突的地址H(key)重新求得求得一个地址序列,通过如下的公式:
H0 = H(key)
Hi = ( H(key) + di) MOD m
H0, H1, H2, …, Hs 1≤ s≤m-1
- Hi 为第i次冲突的地址
- H(key)为Hash函数值
- m 为Hash表表长
- di 为增量序列
对于di的取法有是三种,如下图:

由于并不复杂我们以线性探测再散列举例:
关键字 { 19, 01, 23, 14, 55, 68, 11, 82, 36 }
设定哈希函数 H(key) = key MOD 11 ( 表长=11 )
选用线性探测再散列处理冲突
- 19/11=7 没有冲突 放入表中
- 1/11=1 没有冲突 放入表中
- 23/11=1 产生冲突 1的位置已经存放了。使用函数 Hi = ( H(key) + di) MOD m,第一次冲突di取1 H1 = ( H(key) + di) MOD m=(23+1)mod 11=2 放入2
- 依次类推 冲突一次 di依次取 1 2 3 4 5(实际意义就是往右边找空格子)
- 最终结果如下,下方数次表示第几次成功

- 计算ASL(成功)=(1+1+2+1+3+6+2+5+1)/9
- 计算ASL(失败)=(9+8+7+6+5+4+3+2+1)/9(假设格子如图占完 余数从0~8要查找几次后再能解决冲突 得到了如上数字计算)
7.6.2 再哈希法
第一次冲突使用RH1哈希函数
第二次冲突使用RH2哈希函数
…
每次对应不同的哈希函数

7.6.3 链地址法
7.6.4 公共溢出区法
7.7 哈希表查找代码实现及实例
思想:
- 给定K值,根据构造表时所用的哈希函数求哈希地址j
- 若此位置无记录, 则查找不成功;否则比较关键字,若和给定的关键字相等则成功; 否则根据构造表时设定的冲突处理的方法计算“下一地址”, 重复2)
Status SearchHash(HashTable H, KeyType key, int &p, int &c){
/*在开放定址哈希表H中查找关键字为key的数据*/
/*用c记录发生冲突的次数,初值为0*/
p=Hash(k); /*求哈希地址*/
while(H.data[p].key!=NULL && H.data[p].key!=key)
/*该位置填有数据且与所查关键字不同*/
collision(p, ++c); /*求下一探查地址p*/
if(H.data[p].key==key )
return SUCCESS; /*查找成功,p返回待查数据元素位置*/
else return UNSUCCESS; /*查找不成功,p返回插入位置*/
}
Status InsertHash(HashTable &H, DataType e){
/*查找不成功时在H中插入数据元素e,并返回SUCCESS*/
/*若冲突次数过大,则重建哈希表*/
c=0;
if(SearchHash (H, e.key, p, c))
return UNSUCCESS; /*数据已在哈希表中,不需插入*/
else if(c<hashsize[H.sizeindex]/2){
H.data[p]=e; ++H.count; /*次数c还未达到上限,插入e*/
return SUCCESS;
}
else {
RecreatHashTable(H); /*重建哈希表,当哈希表用了一半以上的空间*/
return SUCCESS;
}
}
7.8 哈希查找性能分析

哈希表的平均查找长度是装填因子 α 的函数,而不是 n 的函数。这说明,用哈希表构造查找表时,可以选择一个适当的装填因子 α,使得平均查找长度限定在某个范围。
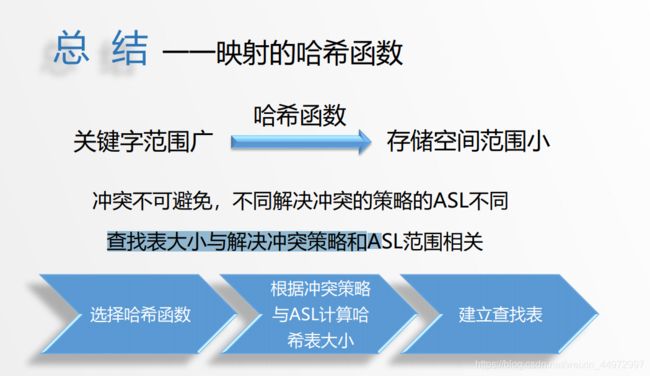
- 选择哈希函数
- 给定平均查找长度
- 根据冲突策略(随机探测 线性探测 链地址)选择对应的公式求出α装载因子
- 由装载因子和我们关键字(数据)个数求的表长 装载因子=关键字个数/表长
- 建立查找表
总结
内容较多,可能有所遗漏和错误的地方,欢迎指出。
附带一本热销的电子书配套适用更佳,链接如下
大话数据结构
提取码:mazy往期文章
绪论-数据结构的基本概念
绪论-算法
线性表-顺序表和链式表概念及其代码实现