蓝桥杯练习

蓝桥杯训练：http://dasai.lanqiao.cn/

查看python标准库：https://docs.python.org/3.6/

蓝桥杯VIP习题练习：https://www.dotcpp.com/oj/problemset.php?page=19&tdsourcetag=s_pctim_aiomsg

桥本分数式：

日本数学家 桥本吉彦教授 于1993年10月在我国山东举行的中日美三国数学教育研讨会上向与会者提出以下填数趣题： 把1，2，……，9，这9个数字填入下式的9个方格中（数字不得重复），使下面的分数等式成立：

口/口口 + 口/口口 = 口/口口
桥本教授当即给出了一个解答，这一填数趣题的解是否唯一？如果不唯一究竟有多少个解？试求出所有解答（等式左边两边分数交换次序只算一个解答）；
全排列：1.生成树 2.递归 3.库函数

生成树：就是在保证原有数据的顺序不变（12），然后把（3)放入数据的1，2号位（123，312）。

排列直接引用库函数

itertools.permutations(sequence,n)

从sequence中拿出n个数做排列，不放回的拿出,n只能小于等于sequence的长度，否则没有输出。

itertools.combinations(sequence,n)

从sequence中拿出n个数做组合，相当于不放回，当n大于sequence的长度自然没有数据。

import iterools

for  item in itertools.permutations(['a','b'],'c'):

       print(item)

permutations函数是根据他们的位置来计算组合的，而不是他们的值.所以有重复的结果。

permutataions（）参数的意义：[n个数，m]，n个数选m个排列

口/口口 + 口/口口 = 口/口口

a1/m+a2/n=a3/p

-->a1np+a2mp=a3mn

坑点：可能存在对称的情况。

​
import itertools
sum = 0
for i in itertools.permutations([1,2,3,4,5,6,7,8,9]):
    a = int(i[0])
    b = int(i[1])
    c = int(i[2])
    d = int(i[3])
    e = int(i[4])
    f = int(i[5])
    g = int(i[6])
    h = int(i[7])
    i = int(i[8])
    if (a*(e*10+f)*(h*10+i)+d*(b*10+c)*(h*10+i)==g*(b*10+c)*(e*10+f)):
        sum+=1
print(sum/2)

​

answer：10

1/26+5/78=4/39
1/32+5/96=7/84
1/32+7/96=5/48
1/78+4/39=6/52
1/96+7/48=5/32
2/68+9/51=7/34
2/68+9/34=5/17
4/56+7/98=3/21
5/26+9/78=4/13
6/34+8/51=9/27
 

凑算式：

       B      DEF
A + — + -——— = 10
       C       GHI

（如果显示有问题，可以参见【图1.jpg】）

这个算式中A~I代表1~9的数字，不同的字母代表不同的数字。

比如：
6+8/3+952/714 就是一种解法，
5+3/1+972/486 是另一种解法。

这个算式一共有多少种解法？（answer:29)

注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。
解析：此题同样是全排列（生成9的全排列）

import itertools
sum = 0
for i in itertools.permutations([1,2,3,4,5,6,7,8,9],9):
    a = int(i[0])
    b = int(i[1])
    c = int(i[2])
    d = int(i[3])
    e = int(i[4])
    f = int(i[5])
    g = int(i[6])
    h = int(i[7])
    i = int(i[8])
    if a + (b/c) + (d*100+e*10+f)/(g*100+h*10+i) ==10:
        sum += 1
print(sum)

方格填数：

 

如图，如下的10个格子，填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）一共有多少种可能的填数方案？
请填写表示方案数目的整数。(answer:1580)

      a0，a1,a2

a3,a4,a5,a6

a7,a8,a9

判定条件：左右|ai-ai+1|!=1 0-11-2 2-3 4-5 5-6 6-7 8-9

                  上下|ai-ai+4|!=1 

                   对角|ai-ai+5|!=1 

               反对角|ai-ai+3|!=1 

不要忘记反对角的情况。

代码有点问题

import itertools
sum = 0
for i in itertools.permutations([0,1,2,3,4,5,6,7,8,9]):
   flag = 0
   for j in range(9):
        if abs(i[j]-i[j+1])==1 and i != 2 and i != 6:
            flag = 1
            break
   if flag==0:
       for j in range(6):
        if abs(i[j]-i[j+4])==1 :
            flag = 1
            break
   if flag==0:
       for j in range(5):
        if abs(i[j]-i[j+5])==1 and i != 2 :
            flag = 1
            break
   if flag==0:
        for j in range(7):
         if abs(i[j]-i[j+3])==1 and i != 3 :
            flag = 1
            break
   if flag==0:
        sum += 1
print(sum)

猜年龄：

美国数学家维纳(N.Wiener)智力早熟，11岁就上了大学。
他曾在1935~1936年应邀来中国清华大学讲学。
一次，他参加某个重要会议，年轻的脸孔引人注目。
于是有人询问他的年龄，他回答说：
“我年龄的立方是个4位数。我年龄的4次方是个6位数。这10个数字正好包含了从0到9这10个数字，每个都恰好出现1次。”
请你推算一下，他当时到底有多年轻。

tips:可以使用计算器和EXCEL

=POWER（）

分析：年龄至少10岁

import itertools
lst = itertools.permutations([0,1,2,3,4,5,6,7,8,9])
for i in lst:
    a,b,c,d,e,f,g,h,i,j = i
    if a != 0 and e != 0:
        age = 10
        while age <= 20:
            if age ** 3 ==(a * 1000 + b * 100 + c * 10 + d) and age ** 4 ==(e * 100000 + f * 10000 + g * 1000 +  h * 100 + i * 10 + j):
                print(age)
                break
            else:
                age += 1
                
                
    

4皇后问题（？）：

规定每个皇后站一行，列是1~4全排列的一种方式

对角线：列差！=行差

2n皇后问题

给定一个n*n的棋盘，棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后，使任意的两个黑皇后都不在同一行、同一列或同一条对角线上，任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法？n小于等于8。

输入格式

　　输入的第一行为一个整数n，表示棋盘的大小。

　　接下来n行，每行n个0或1的整数，如果一个整数为1，表示对应的位置可以放皇后，如果一个整数为0，表示对应的位置不可以放皇后。

输出格式

　　输出一个整数，表示总共有多少种放法。
n皇后与全排列

组合问题

剪邮票：

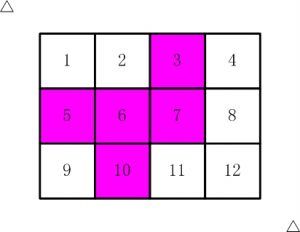
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。 （仅仅连接一个角不算相连）
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

itertools:combinations

从12个数中找5个：

上下：|ai-aj|=4

左右：|ai-aj|=1

排除特殊性

1 2 3 4

6 7 8 9

11 12 13 14

上下差5左右差1

定义两个容器

a:存放原始数据

b:未连通

e.g.2，7，12，13，14

 c:存放连通

2

已连接的点去找未连接的点，当找不到时才能判断没有相连

找到7后，b的个数减少1，原有的7清零，c个数加1，7存放进去

依次进行下去

判断得出选出的5个点是否连通

排列组合

古堡算式

福尔摩斯到某古堡探险，看到门上写着一个奇怪的算式：
ABCDE * ? = EDCBA
他对华生说：“ABCDE应该代表不同的数字，问号也代表某个数字！”
华生：“我猜也是！”
于是，两人沉默了好久，还是没有算出合适的结果来。
请你利用计算机的优势，找到破解的答案。

做法有三：

1.0-9全排列，凑左右两边的整数

left=a0*10000+a1*1000+a2*100+a3*10+a4

right=a4*10000+a3*1000+a2*100+a1*10+a0

?=left/right

判断?是否是小于10的整数

2.先组合再排列

先选5个数再进行全排列，对每一种进行验证等式是否成立

for(i=0,i<9;i++)

     for(j=i+1;j<=9;j++)

          for(k=j+1;k<=9;k++)

全排列itertools

from itertools import permutations

items = ['a', 'b', 'c']
for p in permutations(items):
    print(p)

3.组合的同时排列

for(i=0;i<=9;i++)

    for(j=0;j<=9,j!=i;j++)

 选几个数就是几重循环       

组队
【问题描述】作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员，组成球队的首发阵容。每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1号位至 5 号位的评分之和最大可能是多少？

【解题思路】：答案是290。

蛮力法（枚举法，穷举法，暴力法）

1.找出枚举范围

2.找出约束条件，用逻辑表达式表达出来

e.g.百钱百鸡问题

我国古代数学家张丘建在《算经》一书中提出的数学问题：鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一。百钱买百鸡，问鸡翁、鸡母、鸡雏各几何？

尝试范围即x:1~20,y:1~33,z:1~100

约束条件：x+y+z=100,5x+3y+z/3=100

第三个循环直接不要

z=(100-x-y)/3

for x in range(1,21):
    for y in range(1,34):
        z=100-x-y
        if 5*x+3*y+z/3 == 100:
            print('cock: %s hen :%s poult : %s'%(x,y,z))

递归

斐波拉契数列

比赛尽量避免递归

特殊解法：

差分方程求解法

母函数求解法

减治与变治

全排列

最小公倍数=（m*n/

求最大公约数：a,b两数，假设a>b，a/b=q..r1,r1=0,则公约数为b;b/r1=q...r2,若r2=0,则(a,b)=r1,若r2

假币问题

1、有30枚外观相同的硬币，其中有一枚是假币
2、不知道假币较重还是较轻

海盗喝酒

有一群海盗（不多于20人），在船上比拼酒量。过程如下：打开一瓶酒，
所有在场的人平分喝下，有几个人倒下了。再打开一瓶酒平分，又有倒下的，
再次重复…… 直到开了第4瓶酒，坐着的已经所剩无几，海盗船长也在其中。
当第4瓶酒平分喝下后，大家都倒下了。 等船长醒来，发现海盗船搁浅了。
他在航海日志中写到：“……昨天，我正好喝了一瓶…….奉劝大家，开船不喝酒，喝酒别开船……”
请你根据这些信息，推断开始有多少人，每一轮喝下来还剩多少人。
如果有多个可能的答案，请列出所有答案，每个答案占一行。
1/n1+1/n2+1/n3+1/n4=1

n1>n2>n3>n4

for i in range(2,21):
    for j in range(2,i):
        for k in range(2,j):
            for m in range(2,k):
                sum =1/i + 1/j + 1/k + 1/m
                if sum == 1:
                   print(i,j,k,m,0)

分治法

排序:

归并与快排

快排（分治+快排）

快速排序的基本思想：

任意取一个元素（如第一个）为中心（pivot),所有比它小的元素一律前放，比它大的元素一律后放，形成左右两个子表。

对各子表重新选择中心元素并依此调整，直到每个子表的元素只剩一个。

def quick_sort(data):    
    """快速排序"""    
    if len(data) >= 2:  # 递归入口及出口        
        mid = data[len(data)//2]  # 选取基准值，也可以选取第一个或最后一个元素        
        left, right = [], []  # 定义基准值左右两侧的列表        
        data.remove(mid)  # 从原始数组中移除基准值        
        for num in data:            
            if num >= mid:                
                right.append(num)            
            else:                
                left.append(num)        
        return quick_sort(left) + [mid] + quick_sort(right)    
    else:        
        return data
array = [2,3,5,7,1,4,6,15,5,2,7,9,10,15,9,17,12]
print(quick_sort(array))

def quick_sort(arr):
    n = len(arr)
    if n >= 2:
        pivot = arr[n//2]
        left,right = [],[]
        arr.remove(pivot)
        for num in arr:
           if num >= pivot:
               right.append(num)
           else:
               left.append(num)
        return quick_sort(left) + [pivot] + quick_sort(right)
    else:
       return arr
arr = [int(n) for n in input().split()]
print(quick_sort(arr))

贪婪算法

背包问题

方案1：按物品价值降序装包

方案2：按物品重量升序装包

方案3：按价值与重量比值降序装包

动态规划的最优性原理

https://www.cnblogs.com/mfrank/p/10533701.html

动态规划

对于一个递归结构的问题，如果我们在分析它的过程中，发现了它有很多“重叠子问题”，虽然并不影响结果的正确性，但是我们认为大量的重复计算是不高效的，因此，我们必须将“重叠子问题”进行优化，优化的方法就是“加入缓存”，“加入缓存”的一个学术上的叫法就是“记忆化搜索”。

以斐波拉契为例：

普通算法：

def fib(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fib(n - 1) + fib(n - 2)

根据动态规划的思想，修改如下：

output = [None]*1000 #相当于建立了含有1000个元素的空列表
def fib(n):
    result = output[n]
    if result == None:
        if n==0:
            result =0
        elif n==1:
            result =1
        else:
            result =fib(n-1)+fib(n-2)
        output[n] = result
    return result

动态规划https://blog.csdn.net/qq_25800311/article/details/90635979

有关时间和空间复杂度https://blog.csdn.net/freedom12354/article/details/82119782

求解两个字符串的最长公共子序列https://www.cnblogs.com/mayunting/p/10426316.html