正三角形旋转一周得到的图形是_初二数学研究案例—图形探究篇

疫情期间，学生们居家线上自主学习已成为常态，但是这并不影响同学们自主学习、自主探索，对数学学科的知识进行了更为深入的研究. 

为了让孩子养成勤于思考和探究的良好学习品质，培养他们的数学学科素养.初二年级数学备课组为学生精心设计了极具个性化的线下研究内容：

1. 下发三本数学读物的读后感，之后就某个问题进行深入探讨，展示自己的想法及数学探究过程；

2. 就某个数学问题借助几何画板进行研究，写出研究方案和研究结果，做成图形动画；

3. 课借助《新方法》就学过的某个知识点或方法进行总结(并非例题的简单罗列)有方法总结，有提升，有典型例题，有自己观点；

4. 还可就没学过的数学知识，拿出你的真本事向大家展示，要求同3.

两周之后，学生们的阅读笔记、问题研究、数学模型、高中知识等等，从反馈结果看，他们勤于思考，用心研究,提交了非常多的优秀作品.这些作品围绕了好几个层面开展.

本文汇报第二部分——图形探究(由数学爱好者社团社长彭宇轩、王家钰同学撰稿并归纳整理)

本专题内容共分为四个模块：

一、 阅读手抄报

二、 图形变换        

三、 一些有意思的几何定理

四、函数图像变化规律的探究

我们先来看几位同学的阅读手抄报:   

一、阅读手抄报

陈纬林同学阅读的是《发现几何，一种归纳的方法》，对“线型图案的几何”“雏菊图案”“光效应艺术”“坛场”“伊斯兰艺术”“扭结图案”几种艺术形式，分别绘制图案，图非常漂亮.李奕文同学就这本书谈了自己的感想.

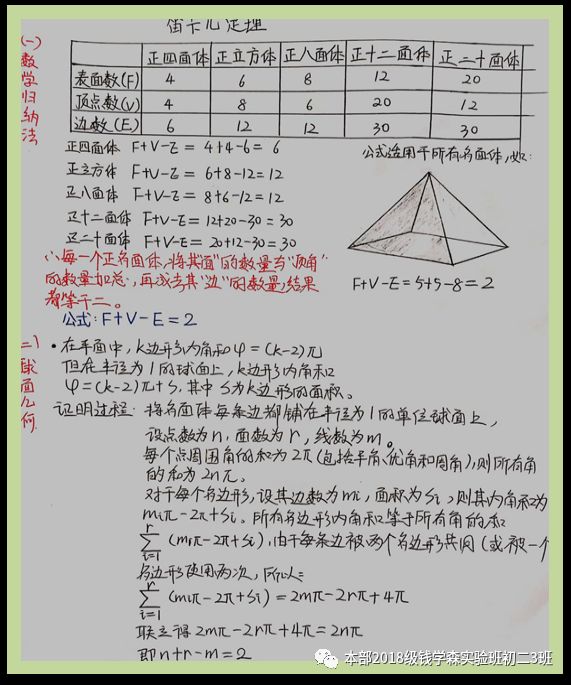
石文玥阅读了《笛卡尔秘密手记》之后，对笛卡尔定理进行了深入研究，从数学归纳法和球面几何两个方面对其进行证明.

    有些同学们借助几何画板这一工具,对图形变换进行了深入的探究,先请大家观看一段视频

二、几何变换

1.借助几何画板解决动点问题

动点问题是初中几何的重点，由于受形象思维和空间概念发展的限制，解这一类题时有一定困难.我先从相对简单的单纯的求入手，通过我做过的一些题来看，有涉及一个动点，两个动点及多个动点的题型.其中，一到两个动点的题较为常见.

一个动点比较大众化的题型特点一般是两定点位于一条直线的同一侧，在直线确定一动点的位置，使动点与两定点线段和最小，求出最小值.

两个动点的题型则可分为两种情况，一是已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最小；二是两动点在两条直线上,定点和其中一个动点共线,求不共线动点分别到定点和另一动点的距离和最小值.

通过观察求线段最值的问题，直接涉及的就是点和线，所以我们采用搬点移线的方法先找到不动的点，结合轴对称性质，确定被“搬”的点，再确定被“移”的线.

当动点与复杂图形结合时，我们就会遇到不单单求线段最值的问题，还会遇到类似求面积，甚至还有求时间t,或需要用含t的代数式表示距离等等，这时候，我们需先将图形化静为动，再利用特殊图形的性质或相互关系，找出等量关系列出方程来解决动点问题.

肖飞同学对动点问题从“动点与线段最值”“动点与特殊图形或面积”两个方面进行了探究，一个动点到多个动点肖飞都进行了细致的研究，最后小结“变化中找不变的”.用特殊图形的性质或相互关系，找出等量关系列出方程来解决动点问题.         ——by肖飞

2. 借助几何画板解决新定义问题

例题：我们定义：如图1，在△ABC中，把AB绕点A顺时针旋转α(0°＜α＜180°)得到AB'，把AC绕点A逆时针旋转β得到AC'，连接B'C'．当α+β＝180°时，我们称△AB'C'是△ABC的“旋补三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．

特例感知

(1)在图2，图3中，△AB'C'是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．

①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD＝BC；

②如图3，当∠BAC＝90°，BC＝8时，则AD长为．

猜想论证

(2)在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．

拓展应用

(3)如图4，在四边形ABCD，∠C＝90°，∠D＝150°，BC＝12，CD＝2，AB＝2．在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．

分析:

王家钰同学归纳了新定义型探究问题的【类型特征】:具有“获取新知识”的意义与特征，它不是单纯的课本知识的应用，而是包含理解和掌握一个“新定义”“新规定”、发现和总结一个“新规律”“新结论”的成份及过程，目的在于考查学生的“学习能力”和“发现与创新”能力.

他认为的解题技巧：

1.多读几遍，深刻理解“新定义",知道新定义是怎么得到的，它的原理，步骤，方法，结论.

2.自己举几个例字，在过程中看自己是否熟练掌握，根据自己举的例子，尝试归纳不同条件下的异同及关系.

3.利用自己学过的知识，把新定义之后的图形类比成自己学过，见过，会做的题.用自己掌握熟练的方法把新定义图形转化成自己熟悉的图形.

4.做题时，先看前提和图，然后再看题以这题为例.

前几问没什么区别，是一个由特殊到一般的转换，就先看图，把能得到的角度，长度，线段关系，角度关系等都求一下，然后再看题都是让求AD和BC的关系，结论应该也是一样的.

对于第一小问不难得出AB'=AC'=AC=BC=AB,∠AB'D=∠AC'D=30°又知道直角，就能想到斜边中线，所以就知道了AD和AC'的关系第二小问一看就是全等，还知道中线，然后同第一问和第三问的解法，一般情况，没有特殊角度，只有中线，不难想到倍长中线，倍长时候可以得到▲BAC≌▲AB'M.由全等得到边等，进而得出关系.

王家钰同学对几何新定义题型做了探究，从例题入手，总结这类问题的特征，然后得出一般的解题方法.他还为大家提供了几个同种类型的图形问题,欢迎同学们进行自主探索.

练习: 定义：到凸四边形一组对边距离相等，到另一组对边距离也相等的点叫凸四边形的准内点．如图1，PH＝PJ，PI＝PG，则点P就是四边形ABCD的准内点．

(1)如图2，∠AFD与∠DEC的角平分线FP，EP相交于点P．

求证：点P是四边形ABCD的准内点．

(2)分别画出图3平行四边形和图4梯形的准内点．(作图工具不限，不写作法，保留作图痕迹)

(3)判断下列命题的真假，在括号内填“真”或“假”．

①任意凸四边形一定存在准内点．

②任意凸四边形一定只有一个准内点．

近些年中考新定义题层出不穷,其中图形类新定义题是其中较为常见的题型.这种题集探究性、拓展性、应用性于一体,充分体现了对于学生"观察、实践、探究、验证、归纳"的核心素养的考查.几何变换压轴题多以三角形、四边形为主，结合平移、旋转、翻折、类比等变换，而四边形的问题常要转化成三角形的问题来解决，通过证明三角形的全等或相似得到相等的角、相等的边或成比例的边，通过勾股定理计算边长．要熟练掌握特殊四边形的判定定理和性质定理，灵活选择解题方法，注意区分各种四边形之间的关系，正确认识特殊与一般的关系，注意方程思想、对称思想以及转化思想的相互渗透．大致有图形旋转(平移)变换，图形翻折变换，图形类比变换几个常见题型.                        ——by 王家钰  

3. 借助几何画板设计漂亮的几何图形

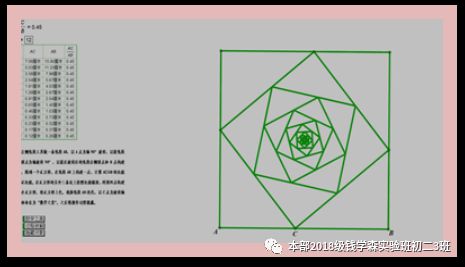
数学给人的印象一直是抽象的.看到同学们绘制的美轮美奂的勾股数、雪花等，我也跃跃欲试，学习制作了正方形迭代旋转构图.轻轻一点动画按钮，无数小正方形有规律地在大正方形中旋转，层层叠叠，宛若繁盛的花朵绽放，仿佛将我带入了艺术世界，让我真切感受到了数学之美 .     

                                             ——by 王嘉毅

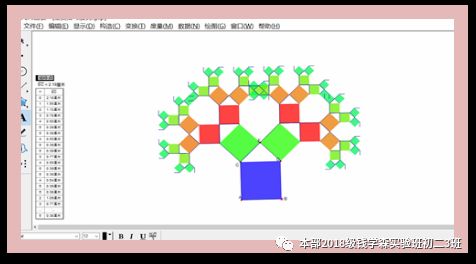
从每一个图中两个较小的正方形出发，又可以分别作出一个第三代的勾股定理图，就这样一生二、二生四、四生八，继续繁殖下去，就长成了大树，整棵大树完全是由勾股定理图形组成的，把它叫做勾股树，名副其实.如果自己动手，画一幅勾股树，填上五彩缤纷的颜色，用来装饰教室里的墙报，或是美化自己的房间，会显得别具一格，自己看了心旷神怡 .                          

                                              ——by 王昊卿

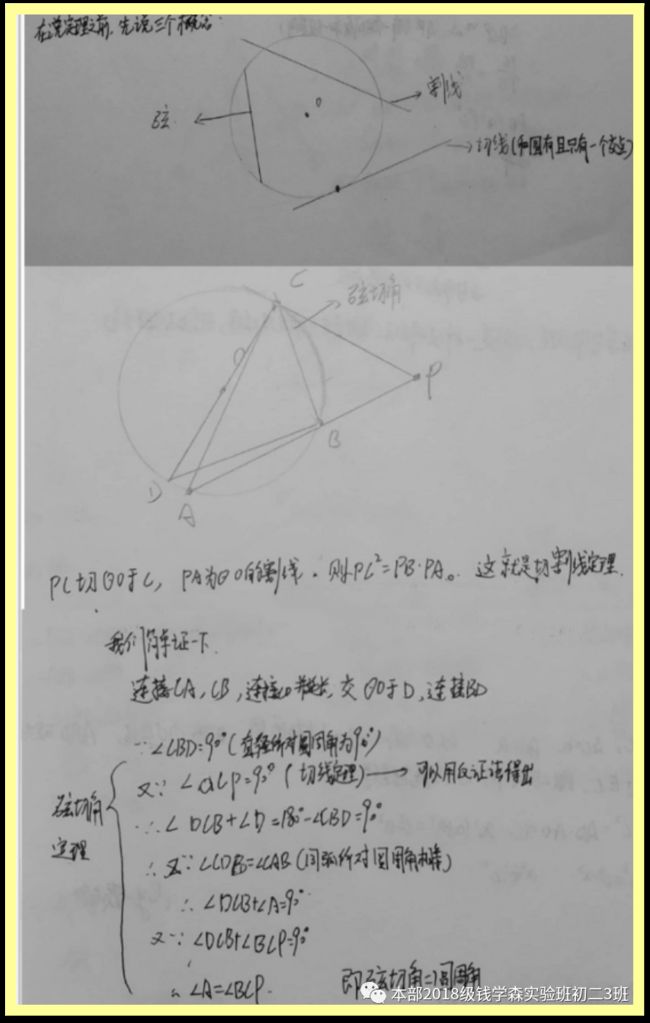
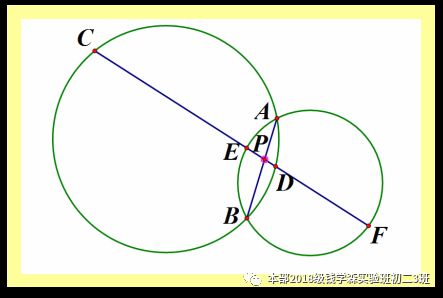
圆幂定理作为圆中的重要结论，是竞赛常考的对象，可以通过圆的性质计算出线段之比，通常在直线几何中通过四点共圆来进行运用.上面三种定理其实是圆幂定理的三种形式，他们其实可以直接用圆幂定理的一般形式来表达.下面，又到了愉快的练习时间(interesting)

已知P点为两圆公共弦AB上的一个点，过P点的一条直线交两圆分别于点C，D，E，F，证明.

2.探索莫雷定理

(1)内角形式

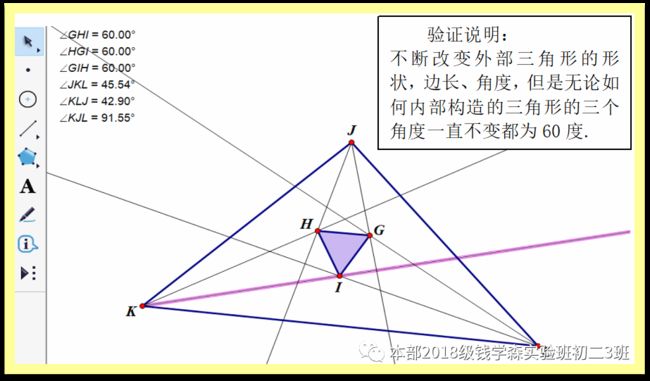
莫雷角三分线定理.将三角形的三个内角三等分，靠近某边的两条三分角线相交得到一个交点，则这样的三个交点可以构成一个正三角形.这个三角形常被称作莫雷正三角形.

验证思路

通过几何画板作图，证明无论三角形如何变换，所构造的三角形一直是正三角形.

定理证明

该定理很漂亮，但是证明非常复杂，困难，以下引用证明如下：

设△ABC中，AQ,AR,BR,BP,CP,CQ为各角的三等分线，三边长为a,b,c,三内角为3α，3β，3γ，则α+β+γ=60°.

在△ABF中，由正弦定理，得AF=csinβ/sin(α+β).

不失一般性，△ABC外接圆直径为1，则由正弦定理，知c=sin3γ，所以AF=(sin3γ*sinβ)/sin(60°-γ)

=[sinβ*sinγ(3-4sin²γ)]/[1/2(√3cosγ-sinγ)]    注：3-4sin²γ=3cos²γ- sin²γ

=2sinβsinγ(√3cosγ+sinγ)=4sinβsinγsin(60°+γ).

同理,AE=4sinβsinγsin(60°+β)

∴AF:AE=[4sinβsinγsin(60°+γ)]：[4sinβsinγsin(60°+β)]=sin(60°+γ):sin(60°+β)=sin∠AEF:sin∠AFE

∴∠AEF=60°+γ,∠AFE=60°+β.同理得，CED=60°+α

FED=180°-CED-(AEF-α-γ)=180°-60°-α-60°+α=60

∴△FED为正三角形.

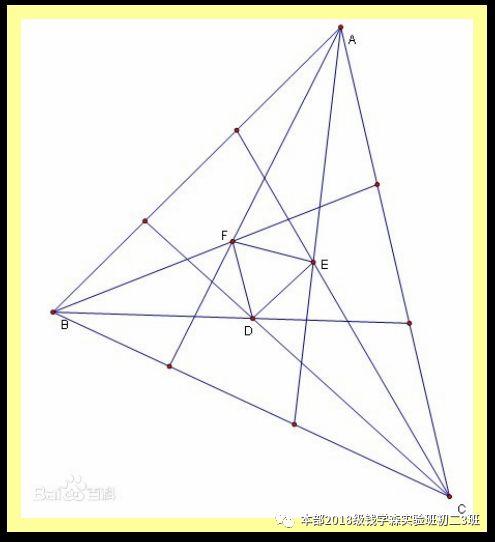
此定理张灵毓同学先借助几何画板进行验证：

又注：此定理有很多证法，下图是她给出的一种证法

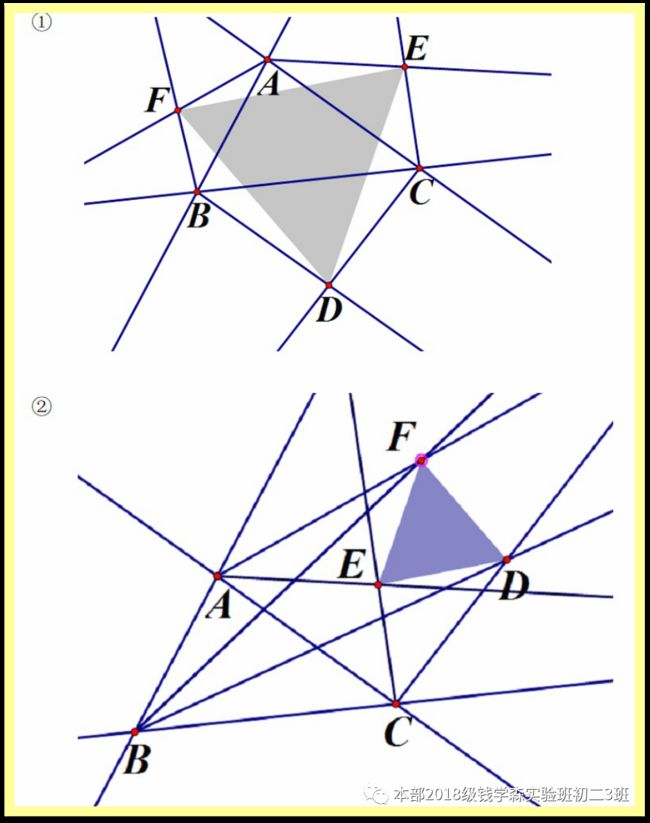
同时，虽然莫雷定理在竞赛中虽不常见，但是作为一个优美数学定理，张灵毓同学还是进行了跟为深入的探讨.它也有很多不同的形式.

(2)外角形式

这两种情况就不再单独证明了，有兴趣的同学可以自行尝试，思路与第一问完全相同.

四、借助几何画板对函数图像变化规律的探究

1.  一次函数：把形如y=kx+b(k，b为常数，且k≠0)的函数叫做一次函数.特别，当b=0时即为正比例函数.一次函数在平面直角坐标系中的图像为一条直线，同学们借助几何画板探究了k，b对一次函数图像的影响，有了非常清晰的直观印象.

2. 二次函数：把形如y=,(a,b,c为常数且a≠0)的函数叫做二次函数.同学们通过在画板中绘制二次函数图形，观察到二次函数图像为一条抛物线，并且通过改变a，b，c的值感受到它们对函数图像影响.并在画图过程中直观感受函数图像的对称性，并且这种表达形式y=对于确定抛物线的顶点和对称轴有非常重要的意义，并且两种表达式之间有非常紧密的关系.

习题答案：

在停课不停学期间，让同学们自己动手动脑，通过自主选择需要解决的问题，自主收集材料，获得自己想要的信息，归纳总结方法，最终内化成自己的知识，这种自主学习能力非常重要.希望同学们相互学习，分享自己的学习成果，提高自主学习能力，为今后的深入学习打好基础.

初二3班班委&家委会

撰稿：彭宇轩 王家钰

视频：彭宇轩 鲍敏颐

                                                    修改：林雪芳