《机器人动力学与控制》第七章—路径规划与避障 7.3 工作空间下使用人工势场法进行路径规划
文章目录
- 7.3.0 前言
- 7.3.1 定义工作空间势场
- 7.3.2 把工作空间下的力映射到关节空间下关节力和扭矩
-
- 例 7.3 一个力加在一个多边形机器人的顶点上
- 例 7.4 两连杆平面机械臂
- 例 7.5 两连杆平面机械臂补充
- 7.3.3 运动规划算法
- 参考引用
7.3.0 前言
一般来说,关节空间下很难获得一个障碍物空间 Q O \mathcal{Q O} QO 完整的表达,因此也很难去评估距离以及距离的变化率。事实上,对于一个曲面,不存在一个描述点到曲面距离的闭合表达式。即便我们能够表达清楚 Q O \mathcal{Q O} QO ,仍然很难获得梯度 ρ \rho ρ 以及梯度变化量 ∇ ρ \nabla \rho ∇ρ。为了解决这些问题,我们将对上一节说到的人工势场法做出一点改进,让势场方程定义在工作空间 W 而不是关节空间 Q。由于工作空间的维度要比关节空间低,因此这也使得在工作空间下应用势场法变得相对容易。
本节我们会先讲解如何一个在工作空间里正确地描述势场,该势场具备关节空间下势场所具备的特点:
- 最低势场处应该在最终目标位形上
- 当机器人接近障碍物的时候,排斥势场急剧地增大
我们会建立一个工作空间下的势场,势场建立好以后,我们会建立一个工作空间梯度到关节变量值的改变的映射,最后我们会介绍一个类似上一节讲到的梯度下降算法,只不过这次运用到具有更加复杂运动学的机器人。
7.3.1 定义工作空间势场
正如之前,定义势场的目标是建立一个使机器人排斥障碍物,并且最小势场点在最终目标位形的势场。在关节空间里这是比较容易理解的,因为在关节空间里,我们用一个n维质点 Q = {q1,q2,q3…qn} 来表达机器人的一个位形,只要Q不经过障碍物位形空间就代表没有碰撞,于是一个复杂的机器人实体被简化成了一个n维质点。这般如此,我们便成功地把一个复杂的物理实体间的接触碰撞问题简化成了n维空间下一系列n维点跟障碍物空间 Q O \mathcal{Q O} QO 是否有交集的问题。但鉴于 Q O \mathcal{Q O} QO 和梯度 ρ \rho ρ 很难在关节空间表达出来,我们又不得不重新考虑在工作空间下描述势场,然而这么做并不容易。因为工作空间下的势场影响的就不是一个n维点了,而是一整个机器人实体。要评估一个势场对于一个实体的影响,那就必定要考虑势场对于整个机械臂的积分计算,这就使得计算变得十分复杂。一个替代做法是选择机器人上的一系列点来进行分析,这些点我们统称为控制点,并且对每个点都要定义相应的工作空间势场。全局势场的获得则是通过把各个独立的势场方程相加得到。评估某个特定的势场对特定控制点的影响与上一节讨论的并无区别,并且梯度的计算也变得更加简单了。
我们用
![]()
来表示机器人上用来定义吸引势场的控制点。对于一个n连杆机械臂,我们可以用各个连杆的质心或者DH坐标系的原点来定义。用
![]()
来表示机器人处于位形 q 的情况下第 i 个控制点 α i \alpha_i αi 的位置。对于每一个
![]()
我们可以定义吸引势场
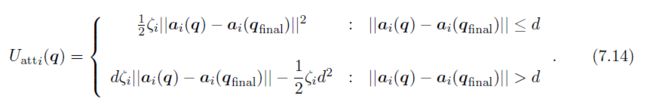
对于单一的点 α i \alpha_i αi ,该势场与上一节工作空间下定义的势场空间类似,它结合了圆锥形势阱和正交势阱,并且在终点位形到达势场全局最小点。如果Aatt包括了合适数量的独立控制点,并且所有的控制点都到达了最小全局势场处,那么机械臂也就到达了终点位形。
有了这样的势场方程,吸引控制点 α i \alpha_i αi 所受到的势场力则为:
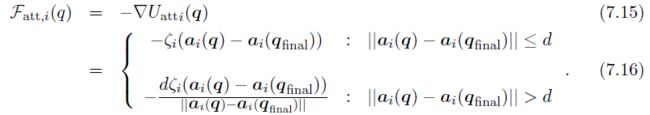
对于排斥势场,在选定了合适的控制点集合之后,势场方程定义为:

其中
![]()
代表控制点距离障碍物最近的距离, ρ 0 \rho_0 ρ0 代表障碍物所能影响的最大距离。每个 U r e p j U_{repj} Urepj 的负梯度则对应了排斥的势场力:

如果b是障碍空间上距离排斥控制点 α j \alpha_j αj 最近的一个点的话,那么
![]()
并且它的梯度为:
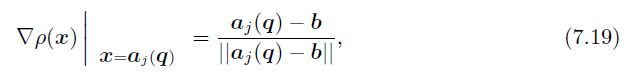
需要注意的是这里排斥控制点的选择并不能保证机器人完全不与障碍物碰撞,下图展示了一个这样的例子:

排斥控制点α1和α2距离障碍物O很远,因此障碍物对α1和α2的排斥力很可能并不足以阻止结构A与障碍物碰撞。原因也十分明显,那就是我们只考虑了整个机械结构里面的两个点的情况,理论上要做到完全避障则需要对于整个结构进行分析。但也不是没有办法解决这个问题,我们可以对每一个连杆各定义一个浮动的排斥控制点
![]()
而这个浮动控制点的位置则定义在一个连杆边缘上最接近障碍物的点,很明显浮动控制点的位置与机器人的位形有关。那么对于上图的例子来说,浮动控制点应该在机器人下边缘E1上,障碍物的正上方处,从而起到排斥障碍物的作用。浮动控制点排斥势场力的定义与其他排斥控制点的定义一样。
7.3.2 把工作空间下的力映射到关节空间下关节力和扭矩
上面我们尝试了在机器人工作空间下建立势场,在这些势场中,机器人各个独立控制点都受到势场所引起的人为定义的势场力。本节我们如何用这些工作空间下的力来推导关节空间下的梯度下降算法。
假设一个力 F \mathcal{F} F 被施加在机械臂的一个点上,这样的力会导致机器人关节受到力和扭矩。如果关节不抵制这些力和扭矩的话,那么就会产生机械臂的运动,这是如何映射工作空间力到关节空间上的运动的关键。我们现在推导机械臂在工作空间受到的力与这个力所引起的关节空间下的力以及扭矩的关系。
用 F F F 表示工作空间力关节受到的力 F \mathcal{F} F 引发的关节力或者扭矩(对于平动关节就是力,对于旋转关节就是扭矩)向量。第九章我们会用虚功原理推导 F F F 和 F \mathcal{F} F 的关系。用 ( δ x , δ y , δ z ) T (\delta x, \delta y, \delta z)^{T} (δx,δy,δz)T 代表工作空间下的虚位移,用 δ q \delta \boldsymbol{q} δq 代表关节空间下的关节虚位移。然后由于虚功是力和位移的内积,通过运用虚位移的知识可知 F ⋅ ( δ x , δ y , δ z ) T = F ⋅ δ q \mathcal{F} \cdot(\delta x, \delta y, \delta z)^{T}=F \cdot \delta \boldsymbol{q} F⋅(δx,δy,δz)T=F⋅δq上式可以写成 F T ( δ x , δ y , δ z ) T = F T δ q \mathcal{F}^{T}(\delta x, \delta y, \delta z)^{T}=F^{T} \delta \boldsymbol{q} FT(δx,δy,δz)T=FTδq回忆雅各比矩阵的知识,我们有 [ δ x δ y δ z ] = J δ q \left[\begin{array}{l} \delta x \\ \delta y \\ \delta z \end{array}\right]=J \delta \boldsymbol{q} ⎣⎡δxδyδz⎦⎤=Jδq(这里的 J J J 是雅各比矩阵描述线速度关系的上面三行),把此式带入到上式得到
F T J δ q = F T δ q \mathcal{F}^{T} J \delta \boldsymbol{q}=F^{T} \delta \boldsymbol{q} FTJδq=FTδq
该式子对任意虚位移 δ q \delta \boldsymbol{q} δq 都成立,因此 F T J = F T \mathcal{F}^{T} J=F^{T} FTJ=FT J T F = F J^{T} \mathcal{F}=F JTF=F这下我们成功的把工作空间下的力与关节力(扭矩)联系在了一起(这是又推导了一遍雅各比静力关系?)
例子地细节以后有空再补充
例 7.3 一个力加在一个多边形机器人的顶点上
例 7.4 两连杆平面机械臂
例 7.5 两连杆平面机械臂补充
7.3.3 运动规划算法
得到了关节空间下的力之后,我们就可以用上一节提到的梯度下降算法来规划我们的轨迹。同样地,该算法里面有很多参数需要我们仔细选取:
- ζ i \zeta_{i} ζi
ζ i \zeta_{i} ζi 定义了吸引场对控制点 α i \alpha_i αi 的影响,不同的 ζ i \zeta_{i} ζi 可以取不一样的值。通常情况下我们选取其中一个 ζ i \zeta_{i} ζi 使其比其他 ζ \zeta ζ 大得多,这样机器人首先会优先到达这个 ζ i \zeta_{i} ζi ,然后相对慢一些地调整轨迹,使其他控制点也到达对应的终值位置。 - η j \eta_{j} ηj
η j \eta_{j} ηj定义了排斥场对控制点 α i \alpha_i αi 的影响,不同的 η j \eta_{j} ηj可以取不一样的值。通常我们设置最终位置的 η j \eta_{j} ηj值相对于其他 η j \eta_{j} ηj非常小,避免机器人由于排斥场的影响远离目标位置。 - ρ 0 \rho_0 ρ0
ρ 0 \rho_0 ρ0 定义了对不同障碍下,场能产生作用的最大距离。通常我们不希望任何障碍物影响到最终位置的任何控制点,同时也希望不同排斥场的之间的影响互不重合。
参考引用
翻译自《robot dynamics and control》
作者:Mark W Spong,Seth Hutchinson, and M. Vidyasagar