机器学习概览2
-什么是机器学习?
机器学习就是一段可以从经验中学习计算机程序,关于一些任务T和以及程序在任务T中的表现的性能评估P,程序能随着经验不断的提升性能。
-更多关于机器学习的定义
机器学习是一门让计算机在不被明确编程的情况下行动的科学。---吴恩达
机器学习是一项能帮助计算机从现有数据中学习,以便预测未来的行为,结果和趋势的数据科学技术。---微软
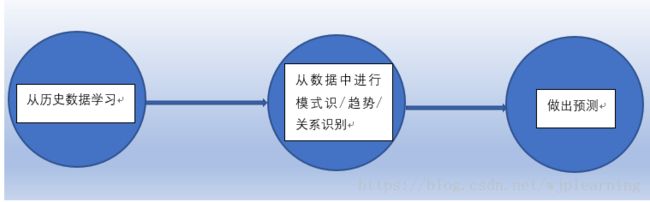
-机器学习利用历史数据进行预测
-机器学习是如何工作的
-机器学习任务的案例
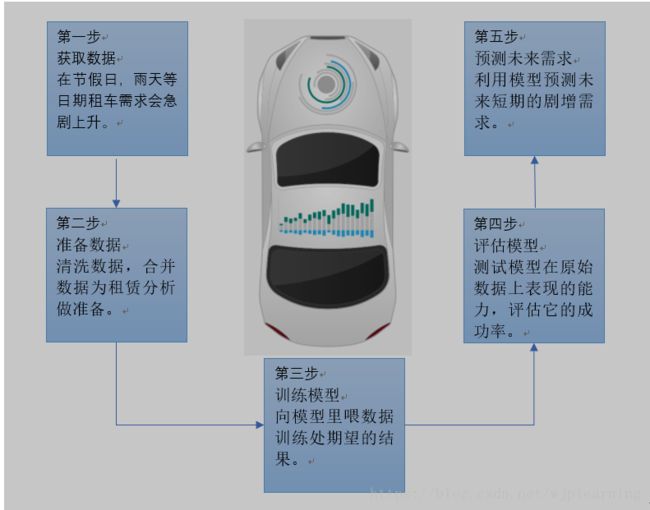
让我们讨论一下你的租赁汽车?
你如何能准确预测对你租车产品的需求呢?
你需要的是如下回归分析
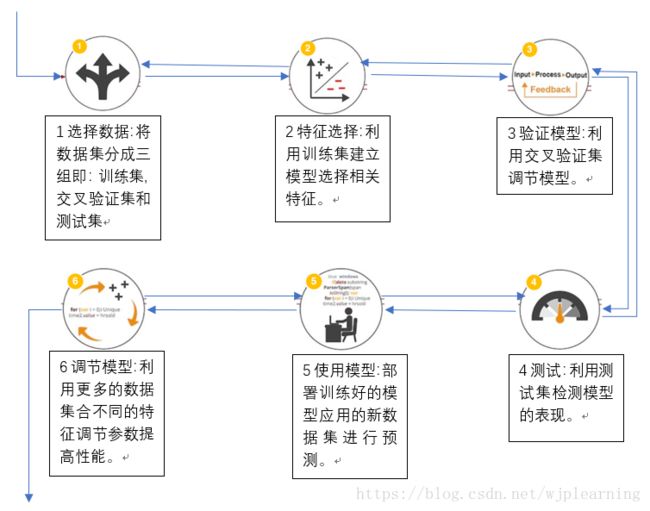
-建立机器学习解决方案的步骤
-传统方法和机器学习方法的区别
-其他相关定义
机器学习就是利用历史数据进行预测。
机器学习和数据挖掘非常相似,数据挖掘是一门在数据中发现未知规则的和关系的学科,而机器学习则是根据先前推断出的知识,利用新的数据在现实生活应用场景中做出预测的学科。
- 从历史数据中计算出近似复杂的函数
- 规则不是清晰定义的而是从数据中学习得来的。
-什么时候应该使用机器学习呢?
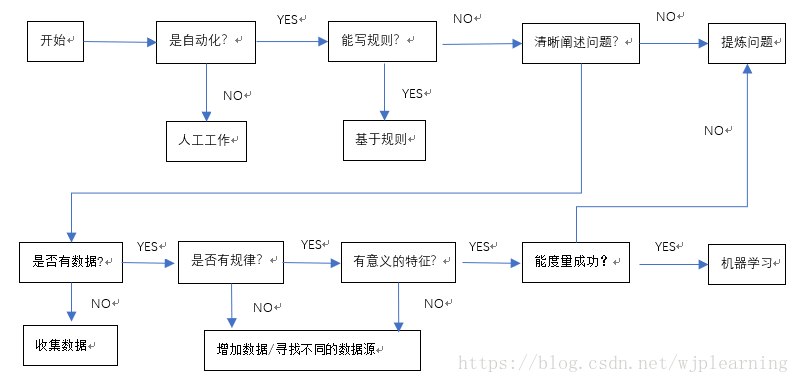
从商业问题到机器学习问题:一份食谱:一步一步把商业问题转化为机器学习问题。
- 你需要机器学习吗?
- 你能清晰的阐述你的问题吗?
- 你有足够多的样本吗?
- 你的问题有一个通用的模式吗?
- 你能发现有代表性意义的数据吗?
- 你如何定义成功?
-商业问题转换为机器学习问题的食谱
什么时候用机器学习?
问题模式化
收集数据
数据中的规律
代表性和特征
评估成功
商业问题转机器学习问题流程
-应用案例:自然语言处理
案例1:支持票分类
- 你需要机器学习吗?
- 大量的支持票
- 人类语言非常复杂和模棱两可的
- 你能清晰的阐述问题吗?
- 给定一个客户的支持票,预测他的服务类型
- 输入:客户支持票;输出:服务类别
- 你有足够的样本吗?
- 大量来自支持票系统的带有服务类别的客户支持票
- 你的问题有一个常规模式吗?
- 日常客户问题会有很多票
- 这些问题常伴随着常用词,例如:账单或者支付会经常出现在具有支付类型的支持票里
- 你能找到具有代表意义的数据吗?
- 利用词向量代表客户支持票
- 标签就是客户支持票的类型
- 你如何定义成功呢?
- 度量服务类型预测准确率
案例2:零售货架分析
给定一张零售货架图片,检测图片中出现的所有商品并与计划布局进行比较。
- 你需要机器学习吗?
- 每天大量人为调节商品货架
- 利用简单的规则检测货架中不可能的商品
- 你能清晰的阐述问题吗?
- 给定一个货架图片,首先检测商品然后与计划的货架布局对比他们的位置
- 输入:图片;输出:商品包装边界
- 你有足够的样本吗?
- 收集大量的零售货架图片并认为的指定商品包装边界标签
- 你的问题有一个常规模式吗?
- 商品包装具有固定的形状,颜色和商标
- 你能找到具有代表意义的数据吗?
- 将图片装换为像素数组
- 带有商品补丁的图片为正样本,随机商品补丁的是负样本
- 你如何定义成功呢?
- 度量商品边界的准确率和召回率
- 盒子和检测到的布局与真实布局的相似性
-什么时候应该使用机器学习呢?
当你有一个包含大量数据和变量的非常复杂的任务或者问题,但是没有一个通用的公式或者方程时,可以考虑使用机器学习。例如:如果你碰到如下问题,那么机器学习是一个不错的选择:
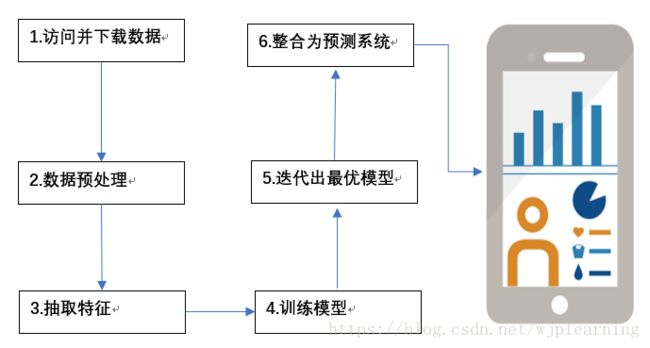
-机器学习步骤
-如何创建机器学习模型
-机器学习工作流
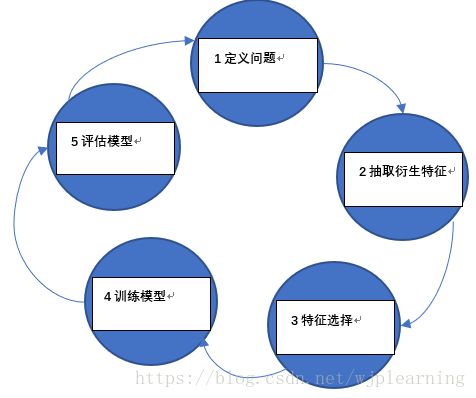
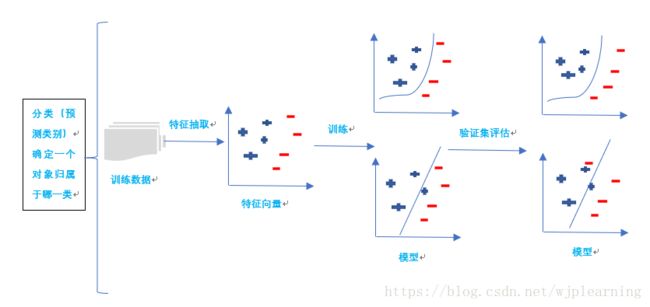
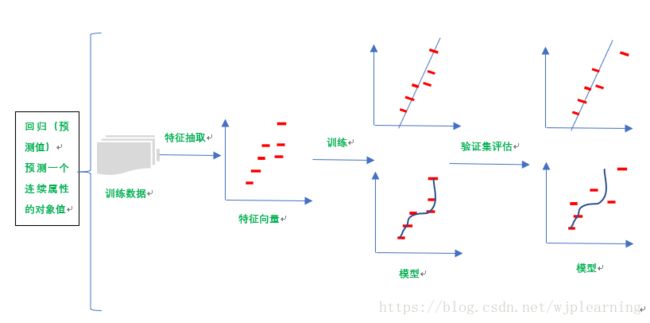
-经典机器学习任务
-案例:如何利用简单模型预测结果
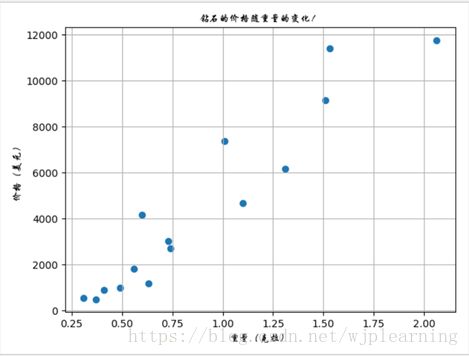
例如:预测钻石的价格
假设我想购买一块钻石,然后你有一个关于钻石会花费多少钱的想法。我带着笔和笔记本来到珠宝店,我几下了所有钻石的价格和它的克拉数,从第一颗钻石开始:他有1.01克拉重价格是7366美元。现在我也记录了其他珠宝店的钻石价格可克拉数。
价格表如下:
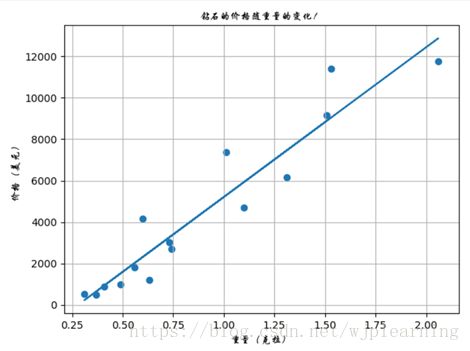
从散点图可以看出钻石的价格随重量的增加而增高,而且具有一定的线性关系,所以我们可以通过绘制一条直线来建立一个模型,以预测未知重量钻石的价格。事实上并不是所有点都能很好的拟合一条直线,而数据科学家给出的解释是:每一个点具有一些噪声或者方差的线性模型。
完美的模型能拟合所有的点,但是现实世界里总是充满噪声和不确定性。因为完美师徒回答钻石花费多少的问题,是预测一个值,所以叫做回归,而完美用的是一条直线进行预测所以又叫做线性回归。拟合曲线如下图:
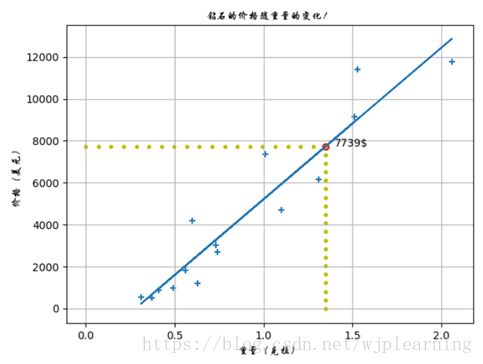
利用模型去寻找答案:
现在我们已经有了一个模型,利用这个模型就可以回答1.35克拉的钻石到底花费多少。为了回答这个问题,我们沿着1.35作一条垂直线与模型直线相交,然后根据焦点作一条水平线与Y轴相交,焦点则是我们要的结果7739美元。哇哦:那么答案就是1.35克拉的钻石应该花费你7739美元。
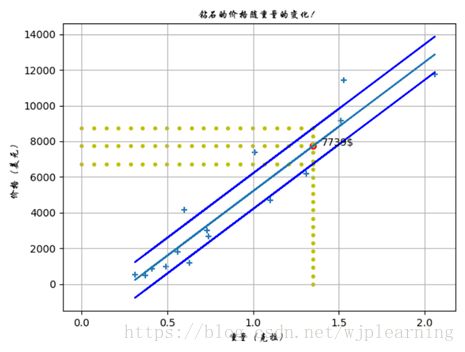
创建一个置信区间:虽然经过努力我们预测出1.35克拉的钻石需要花费大概7739美元,但是很自然的我们希望知道这个预测结果的精确度能达到多少?知道1.35克拉的钻石价格是非常接近7739还是高于或者低于这个价格是非常有用的。为了画出这个结果,我们可以画出一个围绕回归线的信封,包含了大部分的数据点,这个信封叫做我们的置信区间:我们非常确信价格会落在这个信封之内,因为过去他们中的大多数都有。我们可以从1.35克拉的直线画两条水平线。穿过那个信封的顶部和底部。
现在我们可以说一些关于置信区间的事情:我们可以自信的说1.35克拉的钻石价格可能是7739美元,但是它也可能低至6300美元或者高至9000美元。
最终代码:
# -*- coding=UTF-8 -*-
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
def plot_scatter(k, b):
font = matplotlib.font_manager.FontProperties(fname='C:\Windows\Fonts\STXINGKA.TTF')
weight = [1.01, 0.49, 0.31, 1.51, 0.37, 0.73, 1.53, 0.56, 0.41, 0.74, 0.63, 0.6, 2.06, 1.1, 1.31]
price = [7366, 985, 544, 9140, 493, 3011, 11413, 1814, 876, 2690, 1190, 4172, 11764, 4682, 6172]
plt.plot(weight, k*weight + b)# 回归曲线
plt.plot(weight, k * weight + b +1000, c='b')
plt.plot(weight, k * weight + b -1000, c='b')
plt.scatter(1.35, k * 1.35 + b, marker='o', c='r')
plt.text(1.4, k * 1.35 + b, s="%d$" % int(k * 1.35 + b))
plt.scatter(np.linspace(0, 1.35, 20), [8740] * 20, marker='.', c='y')
plt.scatter(np.linspace(0, 1.35, 20), [int(k * 1.35 + b)]*20, marker='.', c='y')
plt.scatter([1.35]*20, np.linspace(0, 8740, 20), marker='.', c='y')
plt.scatter(np.linspace(0, 1.35, 20), [6740] * 20, marker='.', c='y')
plt.scatter(weight, price, marker='+')
plt.xlabel("重量(克拉)", fontproperties = font)
plt.ylabel("价格(美元)", fontproperties = font)
plt.title("钻石的价格随重量的变化!", fontproperties = font)
plt.grid()
plt.show()
def lr():
weight = [1.01, 0.49, 0.31, 1.51, 0.37, 0.73, 1.53, 0.56, 0.41, 0.74, 0.63, 0.6, 2.06, 1.1, 1.31]
price = [7366, 985, 544, 9140, 493, 3011, 11413, 1814, 876, 2690, 1190, 4172, 11764, 4682, 6172]
model = LinearRegression()
model.fit(X=[[e] for e in weight], y=price)
k, b = model.coef_, model.intercept_
plot_scatter(k, b)
if __name__ == '__main__':
lr()
小结:紧接上一篇,继续介绍了一些机器学习的应用场景,然后从机器学习的经典定义开始着重分析了机器学习建模流程,和机器学习的典型任务分类和回归。最后给了一个回归任务的例子,根据钻石的重量价格数据预测给定重量情况下钻石价格,例子里提出了置信区间的概念,是一个衡量机器学习任务的度量,最后的代码是利用sklearn库对数据进行线性回归建模计算出拟合曲线的斜率和截距,然后绘制散点图和置信区间。