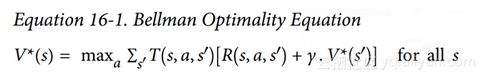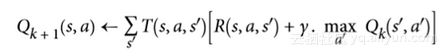【翻译】Sklearn与TensorFlow机器学习实用指南 —— 第16章 强化学习（中）

评价行为：信用分配问题

如果我们知道每一步的最佳动作，我们可以像通常一样训练神经网络，通过最小化估计概率和目标概率之间的交叉熵。这只是通常的监督学习。然而，在强化学习中，智能体获得的指导的唯一途径是通过奖励，奖励通常是稀疏的和延迟的。例如，如果智能体在 100 个步骤内设法平衡杆，它怎么知道它采取的 100 个行动中的哪一个是好的，哪些是坏的？它所知道的是，在最后一次行动之后，杆子坠落了，但最后一次行动肯定不是完全负责的。这被称为信用分配问题：当智能体得到奖励时，很难知道哪些行为应该被信任（或责备）。想想一只狗在行为良好后几小时就会得到奖励，它会明白它得到了什么回报吗？

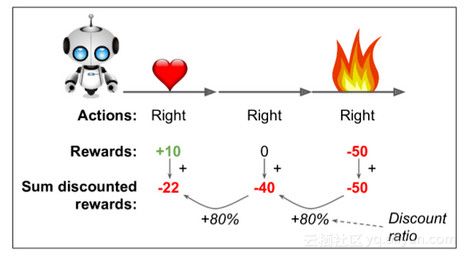
为了解决这个问题，一个通常的策略是基于这个动作后得分的总和来评估这个个动作，通常在每个步骤中应用衰减率r。例如（见图 16-6），如果一个智能体决定连续三次向右，在第一步之后得到 +10 奖励，第二步后得到 0，最后在第三步之后得到 -50，然后假设我们使用衰减率r=0.8，那么第一个动作将得到10 +r×0 + r2×(-50)=-22的分述。如果衰减率接近 0，那么与即时奖励相比，未来的奖励不会有多大意义。相反，如果衰减率接近 1，那么对未来的奖励几乎等于即时回报。典型的衰减率通常为是 0.95 或 0.99。如果衰减率为 0.95，那么未来 13 步的奖励大约是即时奖励的一半（0.9513×0.5），而当衰减率为 0.99，未来 69 步的奖励是即时奖励的一半。在 CartPole 环境下，行为具有相当短期的影响，因此选择 0.95 的折扣率是合理的。

当然，一个好的动作可能会伴随着一些坏的动作，这些动作会导致平衡杆迅速下降，从而导致一个好的动作得到一个低分数（类似的，一个好行动者有时会在一部烂片中扮演主角）。然而，如果我们花足够多的时间来训练游戏，平均下来好的行为会得到比坏的更好的分数。因此，为了获得相当可靠的动作分数，我们必须运行很多次并将所有动作分数归一化（通过减去平均值并除以标准偏差）。之后，我们可以合理地假设消极得分的行为是坏的，而积极得分的行为是好的。现在我们有一个方法来评估每一个动作，我们已经准备好使用策略梯度来训练我们的第一个智能体。让我们看看如何。

策略梯度

正如前面所讨论的，PG 算法通过遵循更高回报的梯度来优化策略参数。一种流行的 PG 算法，称为增强算法，在 1929 由 Ronald Williams 提出。这是一个常见的变体：

首先，让神经网络策略玩几次游戏，并在每一步计算梯度，这使得智能体更可能选择行为，但不应用这些梯度。

运行几次后，计算每个动作的得分（使用前面段落中描述的方法）。

如果一个动作的分数是正的，这意味着动作是好的，可应用较早计算的梯度，以便将来有更大的的概率选择这个动作。但是，如果分数是负的，这意味着动作是坏的，要应用负梯度来使得这个动作在将来采取的可能性更低。我们的方法就是简单地将每个梯度向量乘以相应的动作得分。

最后，计算所有得到的梯度向量的平均值，并使用它来执行梯度下降步骤。

让我们使用 TensorFlow 实现这个算法。我们将训练我们早先建立的神经网络策略，让它学会平衡车上的平衡杆。让我们从完成之前编码的构造阶段开始，添加目标概率、代价函数和训练操作。因为我们的意愿是选择的动作是最好的动作，如果选择的动作是动作 0（左），则目标概率必须为 1，如果选择动作 1（右）则目标概率为 0：

y = 1. - tf.to_float(action)

现在我们有一个目标概率，我们可以定义损失函数（交叉熵）并计算梯度：

learning_rate = 0.01
cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(                    labels=y, logits=logits) 
optimizer = tf.train.AdamOptimizer(learning_rate) 
grads_and_vars = optimizer.compute_gradients(cross_entropy)

注意，我们正在调用优化器的compute_gradients()方法，而不是minimize()方法。这是因为我们想要在使用它们之前调整梯度。compute_gradients()方法返回梯度向量/变量对的列表（每个可训练变量一对）。让我们把所有的梯度放在一个列表中，以便方便地获得它们的值：

gradients = [grad for grad, variable in grads_and_vars]

好，现在是棘手的部分。在执行阶段，算法将运行策略，并在每个步骤中评估这些梯度张量并存储它们的值。在多次运行之后，它如先前所解释的调整这些梯度（即，通过动作分数乘以它们并使它们归一化），并计算调整后的梯度的平均值。接下来，需要将结果梯度反馈到优化器，以便它可以执行优化步骤。这意味着对于每一个梯度向量我们需要一个占位符。此外，我们必须创建操作去应用更新的梯度。为此，我们将调用优化器的apply_gradients()函数，该函数接受梯度向量/变量对的列表。我们不给它原始的梯度向量，而是给它一个包含更新梯度的列表（即，通过占位符递送的梯度）：

gradient_placeholders = [] 
grads_and_vars_feed = [] 
for grad, variable in grads_and_vars:       
    gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape())    
    gradient_placeholders.append(gradient_placeholder)  
    grads_and_vars_feed.append((gradient_placeholder, variable))
training_op = optimizer.apply_gradients(grads_and_vars_feed)

让我们后退一步，看看整个运行过程：

n_inputs = 4 
n_hidden = 4 
n_outputs = 1 
initializer = tf.contrib.layers.variance_scaling_initializer()

learning_rate = 0.01
X = tf.placeholder(tf.float32, shape=[None, n_inputs]) 
hidden = fully_connected(X, n_hidden, activation_fn=tf.nn.elu,weights_initializer=initializer)                          
logits = fully_connected(hidden, n_outputs, activation_fn=None,                    weights_initializer=initializer) 
outputs = tf.nn.sigmoid(logits) 
p_left_and_right = tf.concat(axis=1, values=[outputs, 1 - outputs]) 
action = tf.multinomial(tf.log(p_left_and_right), num_samples=1)

y = 1. - tf.to_float(action) 
cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits) 
optimizer = tf.train.AdamOptimizer(learning_rate) 
grads_and_vars = optimizer.compute_gradients(cross_entropy) 
gradients = [grad for grad, variable in grads_and_vars] 
gradient_placeholders = [] 
grads_and_vars_feed = [] 
for grad, variable in grads_and_vars:    
gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape())    gradient_placeholders.append(gradient_placeholder)    
grads_and_vars_feed.append((gradient_placeholder, variable)) 
training_op = optimizer.apply_gradients(grads_and_vars_feed)

init = tf.global_variables_initializer() 
saver = tf.train.Saver()

到执行阶段了！我们将需要两个函数来计算总折扣奖励，给予原始奖励，以及归一化多次循环的结果：

def discount_rewards(rewards, discount_rate):    
    discounted_rewards = np.empty(len(rewards))    
    cumulative_rewards = 0    
    for step in reversed(range(len(rewards))):        
        cumulative_rewards = rewards[step] + cumulative_rewards * discount_rate       discounted_rewards[step] = cumulative_rewards    
    return discounted_rewards

def discount_and_normalize_rewards(all_rewards, discount_rate):       
    all_discounted_rewards = [discount_rewards(rewards) for rewards in all_rewards]       
    flat_rewards = np.concatenate(all_discounted_rewards)    
    reward_mean = flat_rewards.mean()    
    reward_std = flat_rewards.std()    
    return [(discounted_rewards - reward_mean)/reward_std  for discounted_rewards in all_discounted_rewards]

让我们检查一下运行的如何：

>>> discount_rewards([10, 0, -50], discount_rate=0.8) 
array([-22., -40., -50.]) 
>>> discount_and_normalize_rewards([[10, 0, -50], [10, 20]], discount_rate=0.8) 
[array([-0.28435071, -0.86597718, -1.18910299]), array([ 1.26665318,  1.0727777 ])]

对discount_rewards()的调用正好返回我们所期望的（见图 16-6）。你也可以验证函数iscount_and_normalize_rewards()确实返回了两个步骤中每个动作的标准化分数。注意第一步比第二步差很多，所以它的归一化分数都是负的；从第一步开始的所有动作都会被认为是坏的，反之，第二步的所有动作都会被认为是好的。

我们现在有了训练策略所需的一切：

n_iterations = 250      # 训练迭代次数 
n_max_steps = 1000      # 每一次的最大步长 
n_games_per_update = 10 # 每迭代十次训练一次策略网络 
save_iterations = 10    # 每十次迭代保存模型
discount_rate = 0.95
with tf.Session() as sess:    
    init.run()    
    for iteration in range(n_iterations):        
        all_rewards = []    #每一次的所有奖励        
        all_gradients = []  #每一次的所有梯度        
        for game in range(n_games_per_update):            
            current_rewards = []   #当前步的所有奖励        
            current_gradients = [] #当前步的所有梯度 
            obs = env.reset()            
            for step in range(n_max_steps):                
                action_val, gradients_val = sess.run([action, gradients],
                feed_dict={X: obs.reshape(1, n_inputs)}) # 一个obs                
                obs, reward, done, info = env.step(action_val[0][0])                current_rewards.append(reward)                
                current_gradients.append(gradients_val)                
                if done:                    
                    break            
                all_rewards.append(current_rewards)            
                all_gradients.append(current_gradients)
        # 此时我们每10次运行一次策略，我们已经准备好使用之前描述的算法去更新策略，注：即使用迭代10次的结果来优化当前的策略。      
        all_rewards = discount_and_normalize_rewards(all_rewards)        
        feed_dict = {}        
        for var_index, grad_placeholder in enumerate(gradient_placeholders):
            # 将梯度与行为分数相乘，并计算平均值
            mean_gradients = np.mean([reward * all_gradients[game_index][step][var_index] for game_index, rewards in enumerate(all_rewards)  for step, reward in enumerate(rewards)],axis=0)            
            feed_dict[grad_placeholder] = mean_gradients        
        sess.run(training_op, feed_dict=feed_dict)  
        if iteration % save_iterations == 0:           
            saver.save(sess, "./my_policy_net_pg.ckpt")

每一次训练迭代都是通过运行10次的策略开始的（每次最多 1000 步，以避免永远运行）。在每一步，我们也计算梯度，假设选择的行动是最好的。在运行了这 10 次之后，我们使用discount_and_normalize_rewards()函数计算动作得分；我们遍历每个可训练变量，在所有次数和所有步骤中，通过其相应的动作分数来乘以每个梯度向量；并且我们计算结果的平均值。最后，我们运行训练操作，给它提供平均梯度（对每个可训练变量提供一个）。我们继续每 10 个训练次数保存一次模型。

我们做完了！这段代码将训练神经网络策略，它将成功地学会平衡车上的平衡杆（你可以在 Juyter notebook 上试用）。注意，实际上有两种方法可以让玩家游戏结束：要么平衡可以倾斜太大，要么车完全脱离屏幕。在 250 次训练迭代中，策略学会平衡极点，但在避免脱离屏幕方面还不够好。额外数百次的训练迭代可以解决这一问题。

研究人员试图找到一种即使当智能体最初对环境一无所知时也能很好地工作的算法。然而，除非你正在写论文，否则你应该尽可能多地将先前的知识注入到智能体中，因为它会极大地加速训练。例如，你可以添加与屏幕中心距离和极点角度成正比的负奖励。此外，如果你已经有一个相当好的策略，你可以训练神经网络模仿它，然后使用策略梯度来改进它。

尽管它相对简单，但是该算法是非常强大的。你可以用它来解决更难的问题，而不仅仅是平衡一辆手推车上的平衡杆。事实上，AlgPaGo 是基于类似的 PG 算法（加上蒙特卡罗树搜索，这超出了本书的范围）。

现在我们来看看另一个流行的算法。与 PG 算法直接尝试优化策略以增加奖励相反，我们现在看的算法是间接的：智能体学习去估计每个状态的未来衰减奖励的期望总和，或者在每个状态中的每个行为未来衰减奖励的期望和。然后，使用这些知识来决定如何行动。为了理解这些算法，我们必须首先介绍马尔可夫决策过程（MDP）。

马尔可夫决策过程

在二十世纪初，数学家 Andrey Markov 研究了没有记忆的随机过程，称为马尔可夫链。这样的过程具有固定数量的状态，并且在每个步骤中随机地从一个状态演化到另一个状态。它从状态S演变为状态S'的概率是固定的，它只依赖于(S, S')对，而不是依赖于过去的状态（系统没有记忆）。

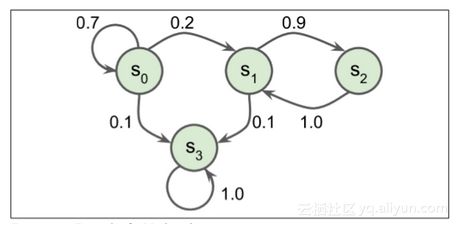
图 16-7 展示了一个具有四个状态的马尔可夫链的例子。假设该过程从状态S0开始，并且在下一步骤中有 70% 的概率保持在该状态不变中。最终，它必然离开那个状态，并且永远不会回来，因为没有其他状态回到S0。如果它进入状态S1，那么它很可能会进入状态S2（90% 的概率），然后立即回到状态S1（以 100% 的概率）。它可以在这两个状态之间交替多次，但最终它会落入状态S3并永远留在那里（这是一个终端状态）。马尔可夫链可以有非常不同的应用，它们在热力学、化学、统计学等方面有着广泛的应用。

马尔可夫决策过程最初是在 20 世纪 50 年代由 Richard Bellman 描述的。它们类似于马尔可夫链，但有一个连结：在状态转移的每一步中，一个智能体可以选择几种可能的动作中的一个，并且转移概率取决于所选择的动作。此外，一些状态转移返回一些奖励（正或负），智能体的目标是找到一个策略，随着时间的推移将最大限度地提高奖励。

例如，图 16-8 中所示的 MDP 在每个步骤中具有三个状态和三个可能的离散动作。如果从状态S0开始，随着时间的推移可以在动作A0、A1或A2之间进行选择。如果它选择动作A1，它就保持在状态S0中，并且没有任何奖励。因此，如果愿意的话，它可以决定永远呆在那里。但是，如果它选择动作A0，它有 70% 的概率获得 10 奖励，并保持在状态S0。然后，它可以一次又一次地尝试获得尽可能多的奖励。但它将在状态S1中结束这样的行为。在状态S1中，它只有两种可能的动作：A0或A1。它可以通过反复选择动作A1来选择停留，或者它可以选择动作A2移动到状态S2并得到 -50 奖励。在状态S3中，除了采取行动A1之外，别无选择，这将最有可能引导它回到状态S0，在途中获得 40 的奖励。通过观察这个 MDP，你能猜出哪一个策略会随着时间的推移而获得最大的回报吗？在状态S0中，清楚地知道A0是最好的选择，在状态S3中，智能体别无选择，只能采取行动A1，但是在状态S1中，智能体否应该保持不动（A0）或通过火（A2），这是不明确的。

Bellman 找到了一种估计任何状态S的最佳状态值的方法，他提出了V(s)，它是智能体在其采取最佳行为达到状态s后所有衰减未来奖励的总和的平均期望。他表明，如果智能体的行为最佳，那么贝尔曼最优性公式适用（见公式 16-1）。这个递归公式表示，如果智能体最优地运行，那么当前状态的最优值等于在采取一个最优动作之后平均得到的奖励，加上该动作可能导致的所有可能的下一个状态的期望最优值。

其中：
T为智能体选择动作a时从状态s到状态s'的概率
R为智能体选择以动作a从状态s到状态s'的过程中得到的奖励
r 为衰减率

这个等式直接引出了一种算法，该算法可以精确估计每个可能状态的最优状态值：首先将所有状态值估计初始化为零，然后用数值迭代算法迭代更新它们（见公式 16-2）。一个显著的结果是，给定足够的时间，这些估计保证收敛到最优状态值，对应于最优策略。

其中：是在k次算法迭代对状态s的估计

该算法是动态规划的一个例子，它将了一个复杂的问题（在这种情况下，估计潜在的未来衰减奖励的总和）变为可处理的子问题，可以迭代地处理（在这种情况下，找到最大化平均报酬与下一个衰减状态值的和的动作）

了解最佳状态值可能是有用的，特别是评估策略，但它没有明确地告诉智能体要做什么。幸运的是，Bellman 发现了一种非常类似的算法来估计最优状态-动作值（state-action values），通常称为 Q 值。状态行动(S, A)对的最优 Q 值，记为Q(s, a)，是智能体在到达状态S，然后选择动作A之后平均衰减未来奖励的期望的总和。但是在它看到这个动作的结果之前，假设它在该动作之后的动作是最优的。

下面是它的工作原理：再次，通过初始化所有的 Q 值估计为零，然后使用 Q 值迭代算法更新它们（参见公式 16-3）。

一旦你有了最佳的 Q 值，定义最优的策略π*(s)，它是平凡的：当智能体处于状态S时，它应该选择具有最高 Q 值的动作，用于该状态。

让我们把这个算法应用到图 16-8 所示的 MDP 中。首先，我们需要定义 MDP：

nan=np.nan  # 代表不可能的动作 
T = np.array([  # shape=[s, a, s']        
    [[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]],
    [[0.0, 1.0, 0.0], [nan, nan, nan], [0.0, 0.0, 1.0]],       
    [[nan, nan, nan], [0.8, 0.1, 0.1], [nan, nan, nan]],    ]) 
R = np.array([  # shape=[s, a, s']        
    [[10., 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]],        
    [[10., 0.0, 0.0], [nan, nan, nan], [0.0, 0.0, -50.]],        
    [[nan, nan, nan], [40., 0.0, 0.0], [nan, nan, nan]],    ]) 
possible_actions = [[0, 1, 2], [0, 2], [1]]

让我们运行 Q 值迭代算法

Q = np.full((3, 3), -np.inf)  # -inf 对应着不可能的动作 
for state, actions in enumerate(possible_actions):    
    Q[state, actions] = 0.0  # 对所有可能的动作初始化为0.0
learning_rate = 0.01 
discount_rate = 0.95 
n_iterations = 100
for iteration in range(n_iterations):   
    Q_prev = Q.copy()    
    for s in range(3):        
        for a in possible_actions[s]:            
            Q[s, a] = np.sum([T[s, a, sp] * (R[s, a, sp] + discount_rate * np.max(Q_prev[sp]))  
            for sp in range(3)])

结果的 Q 值类似于如下：

>>> Q 
array([[ 21.89498982,  20.80024033,  16.86353093],       
        [  1.11669335,         -inf,   1.17573546],       
        [        -inf,  53.86946068,         -inf]]) 
>>> np.argmax(Q, axis=1)  # 每一状态的最优动作
array([0, 2, 1])

这给我们这个 MDP 的最佳策略，当使用 0.95 的衰减率时：在状态S0选择动作A0，在状态S1选择动作A2（通过火焰！）在状态S2中选择动作A1（唯一可能的动作）。有趣的是，如果你把衰减率降低到 0.9，最优的策略改变：在状态S1中，最好的动作变成A0（保持不变；不通过火）。这是有道理的，因为如果你认为现在比未来更重要，那么未来奖励的前景是不值得立刻经历痛苦的。

原文发布时间为：2018-07-08
本文作者：ApacheCN【翻译】
本文来自云栖社区合作伙伴“ Python爱好者社区”，了解相关信息可以关注“ Python爱好者社区”