Opencv基于Python图像轮廓——轮廓绘制及其特征

目标

在本篇文章中，我们将学习到以下内容：

• 了解轮廓是什么
• 学习查找轮廓，绘制轮廓等
• 轮廓入门部分你将学到以下函数：cv.findContours()，cv.drawContours()
• 如何找到轮廓的不同特征，例如面积，周长，质心，边界框等
• 轮廓特征部分你将学习到大量与轮廓有关的功能

1. 轮廓入门

1.1 什么是轮廓

轮廓可以简单地解释为连接具有相同颜色或强度的所有连续点（沿边界）的曲线，轮廓是用于形状分析以及对象检测和识别的有用工具。

• 为了获得更高的准确性，请使用二进制图像。因此，在找到轮廓之前，请应用阈值或canny边缘检测。
• 从OpenCV 3.2开始，findContours()不再修改原图像。
• 在OpenCV中，找到轮廓就像从黑色背景中找到白色物体。因此请记住，一般需要找到的对象应该是白色，背景应该是黑色。

下面让我们看看如何找到二进制图像的轮廓：

代码1.1：

import numpy as np
import cv2 as cv

# 读取图像
img = cv.imread('./data/test.png')
# 灰度化
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# 二值化
ret, thresh = cv.threshold(imggray, 127, 255, 0)
# 轮廓提取
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
# 第三个参数传递值为-1，绘制所有轮廓
cv.drawContours(img, contours, -1, (0, 255, 0), 3)
# cv.drawContours(img, contours, 3, (0, 255, 0), 3)
# cnt = contours[3]
# cv.drawContours(img, [cnt], 0, (0, 255, 0), 3)
# 显示轮廓
cv.namedWindow('drawContours', 0)
cv.imshow('drawContours', img)
cv.waitKey()

findcontour()函数中有三个参数，第一个是原图像，第二个是轮廓检索模式，第三个是轮廓逼近方法，输出等高线和层次结构。轮廓是图像中所有轮廓的Python列表，每个单独的轮廓是一个(x,y)坐标的Numpy数组的边界点的对象。

效果如下图所示：

绘制所有轮廓

注意： 接下来我们将详细讨论第二和第三个参数以及有关层次的结构，在此之前，代码示例中赋予它们的值将适用于所有图像。

1. 2 如何绘制轮廓

要绘制轮廓，请使用cv.drawContours函数。只要有边界点，它也可以用来绘制任何形状，它的第一个参数是原图像，第二个参数是应该作为Python列表传递的轮廓，第三个参数是轮廓的索引（在绘制单个轮廓时有用，要绘制所有轮廓，请传递-1），其余参数是颜色，宽度等等。

• 在图像中绘制所有轮廓：

cv.drawContours(img, contours, -1, (0,255,0), 3)

• 绘制单个轮廓，如第四个轮廓，仅需修改上述第13行代码参数即可：

cv.drawContours(img, contours, 3, (0,255,0), 3)

效果如下图所示：

绘制第四条轮廓

• 但是在大多数情况下，以下方法会很有用：

cnt = contours[3]
cv.drawContours(img, [cnt], 0, (0,255,0), 3)

注意: 最后两种方法相似，但是学习到后面时，你会发现最后一种更有用。

1.3 轮廓近似方法

这是cv.findContours函数中的第三个参数。它实际上表示什么？

上面我们说的是轮廓强度相同形状的边界，它存储形状边界的(x,y)坐标，但是它存储所有坐标吗？其实它是通过轮廓近似方法指定的。

如果传递cv.CHAIN_APPROX_NONE，则将存储所有边界点，但是实际上我们需要所有这些点吗？例如，你找到了一条直线的轮廓。你是否需要线上的所有点来代表该线？不，我们只需要该线的两个端点即可。这就是cv.CHAIN_APPROX_SIMPLE所做的。它删除所有冗余点并压缩轮廓，从而节省内存。

下面的矩形图像演示了此技术，只需在轮廓数组中的所有坐标上绘制一个环（以绿色绘制），第一幅图像显示了我用cv.CHAIN_APPROX_NONE获得的效果（734个点），第二幅图像显示了我用cv.CHAIN_APPROX_SIMPLE获得的效果（只有4个点）。可以看到，它可以节省大量内存！！！

2. 轮廓特征

在本章节部分，我们将学习以下内容：

• 如何找到轮廓的不同特征，例如面积，周长，质心，边界框等
• 实现大量与轮廓有关的功能

2.1 特征矩

特征矩可以帮助计算一些特征，例如物体的质心，物体的面积等，函数cv.moments()提供了所有计算出的矩值的字典。此时，你可以提取有用的数据，例如面积，质心等。

质心由关系给出，$$C_x=\frac{M_{10}}{M_{00}}和C_y=\frac{M_{01}}{M_{00}}$$可以按照以下步骤进行，代码如下（以下接着往代码1.1后面写）：

#轮廓重心
cnt = contours[0]
M = cv.moments(cnt)
print(M)
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
print(cx, cy)

打印结果：

{‘m00’: 68783.5, ‘m10’: 20155656.333333332, ‘m01’: 14859279.833333332, ‘m20’: 6282709635.75, ‘m11’: 4354277664.625, ‘m02’: 3586551591.25, ‘m30’: 2061672731334.2002, ‘m21’: 1357287605165.4, ‘m12’: 1050991274868.0667, ‘m03’: 937472298913.9501, ‘mu20’: 376489652.36095905, ‘mu11’: 56991.3312997818, ‘mu02’: 376505618.5195246, ‘mu30’: 2005762.1354980469, ‘mu21’: 2238986.5301361084, ‘mu12’: -1986528.7002563477, ‘mu03’: -2217792.504638672, ‘nu20’: 0.07957643934309044, ‘nu11’: 1.2045927928746822e-05, ‘nu02’: 0.07957981401764169, ‘nu30’: 1.6164741035372612e-06, ‘nu21’: 1.804433177832962e-06, ‘nu12’: -1.6009735865816214e-06, ‘nu03’: -1.7873525914762914e-06}
293 216

2.2 轮廓面积

轮廓区域由函数cv.contourArea()或从矩 M[‘m00’] 中给出

#轮廓面积
area = cv.contourArea(cnt)
print (area)

打印结果：

68783.5

2.3 轮廓周长

轮廓周长也称为弧长。可以使用cv.arcLength()函数计算得到，第二个参数指定形状是闭合轮廓( True )还是曲线。

#轮廓周长
perimeter = cv.arcLength(cnt,True)
print (perimeter)

打印结果：

981.9036719799042

2.4 轮廓近似

根据我们指定的精度，它可以将轮廓形状近似为顶点数量较少的其他形状，它是Douglas-Peucker算法的实现。

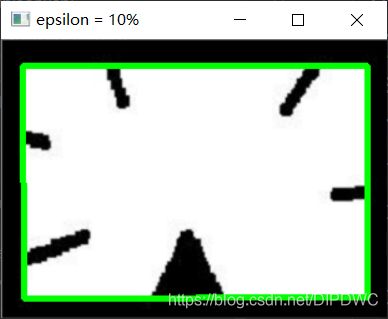
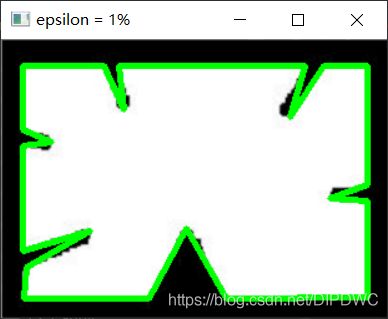
为了理解这一点，假设我们试图在图像中找到一个矩形，但是由于图像中的某些问题，我们没有得到一个完美的矩形，而是一个“坏形状”（如下图所示），现在，你可以使用此功能来近似形状。在这种情况下，第二个参数称为epsilon，它是从原始轮廓到近似轮廓的最大距离。它是一个精度参数，需要正确选择epsilon才能获得正确的输出。

代码2.4：

import numpy as np
import cv2 as cv

img = cv.imread('./data/approximate.png')
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggray, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cv.imshow('img', img2)
cnt = contours[0]
epsilon = 0.1*cv.arcLength(cnt, True)
# epsilon = 0.01*cv.arcLength(cnt, True)
approx = cv.approxPolyDP(cnt, epsilon, True)
cv.polylines(img, [approx], True, (0, 255, 0), 3)
cv.imshow('epsilon = 10% ', img)
# cv.imshow('epsilon = 1% ', img)
cv.waitKey(0)
cv.destroyAllWindows()

下面，在第二张图片中，绿线显示了ε=弧长的10％时的近似曲线。第三幅图显示了ε=弧长度的1％时的情况。第三个参数指定曲线是否闭合。

2.5 轮廓凸包

凸包外观看起来与轮廓近似相似，但不同（在某些情况下两者可能提供相同的结果）。在这里，cv.convexHull()函数检查曲线是否存在凸凹缺陷并对其进行校正。一般而言，凸曲线是始终凸出或至少平坦的曲线，如果在内部凸出，则称为凸度缺陷，例如，检查下面的手的图像，红线显示手的凸包，双向箭头标记显示凸度缺陷，这是凸包与轮廓线之间的局部最大偏差。

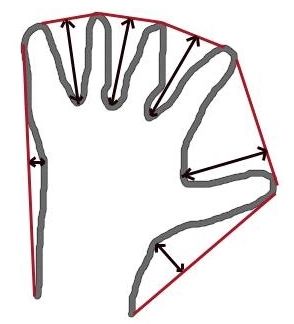
代码2.5：

import numpy as np
import cv2 as cv

img = cv.imread('./data/approximate.png')
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggray, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cv.imshow('img', img2)
cnt = contours[0]
hull = cv.convexHull(cnt)
cv.polylines(img, [hull], True, (0, 255, 0), 3)
cv.imshow('convexHull ', img)
cv.waitKey(0)
cv.destroyAllWindows()

2.6 检查凸度

cv.isContourConvex()具有检查曲线是否凸出的功能，它只是返回True还是False。

#凸性检测
k = cv.isContourConvex(cnt)
print (k)

False

False结果说明上述轮廓没有凸包处。

2.7 边界矩形

有两种类型的边界矩形，一是直边外接矩形，二是旋转矩形(最小外接矩形)。

2.7.1 直边外接矩形

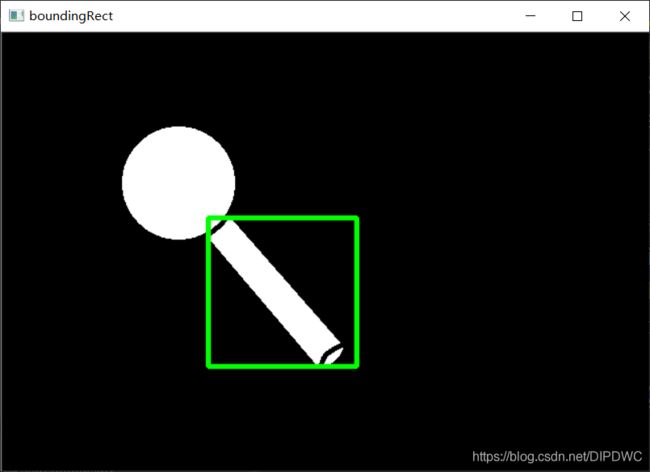
它是一个矩形，不考虑物体的旋转，所以边界矩形的面积不是最小的。它是由函数cv.boundingRect()计算得到。

令(x，y) 为矩形的左上角坐标，而 (w，h)为矩形的宽度和高度。

x,y,w,h = cv.boundingRect(cnt)
cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),3)

代码2.7.1：

import numpy as np
import cv2 as cv

img = cv.imread('./data/boundingRect.png')
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggray, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cnt = contours[1]
# (x, y)为矩形左上角的坐标， (w, h)是矩形的宽和高
x, y, w, h = cv.boundingRect(cnt)
# 直边外接矩形
img_boundingRect = cv.rectangle(img, (x, y), (x+w, y+h), (0, 255, 0), 3)
cv.imshow('boundingRect', img_boundingRect)
cv.waitKey()
cv.destroyAllWindows()

2.7.2 旋转矩形(最小外接矩形)

这里，边界矩形是用最小面积绘制的，所以它也考虑了旋转。使用的函数是
cv.minAreaRect()，它返回一个Box2D结构，其中包含以下细节 (中心(x,y)，(宽度，高度)，旋转角度)。但要画出这个矩形，我们需要矩形的四个角点，它由函数cv.boxPoints()获得。

rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img,[box],0,(0,0,255),3)

代码2.7.2：

import numpy as np
import cv2 as cv

img = cv.imread('./data/boundingRect.png')
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggray, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cnt = contours[1]
# (x, y)为矩形左上角的坐标， (w, h)是矩形的宽和高
x, y, w, h = cv.boundingRect(cnt)
# 直边外接矩形
img_boundingRect = cv.rectangle(img, (x, y), (x+w, y+h), (0, 255, 0), 3)
# cv.imshow('boundingRect', img_boundingRect)
# 最小外接矩形
img_AreaRect = cv.minAreaRect(cnt)
box = cv.boxPoints(img_AreaRect)
box = np.int0(box)
cv.drawContours(img_boundingRect, [box], 0, (0, 0, 255), 3)
cv.imshow('minAreaRect', img_boundingRect)
cv.waitKey()
cv.destroyAllWindows()

如下图所示，两个矩形都显示在一张单独的图像中，绿色矩形显示正常的边界矩形，红色矩形是旋转后的矩形。

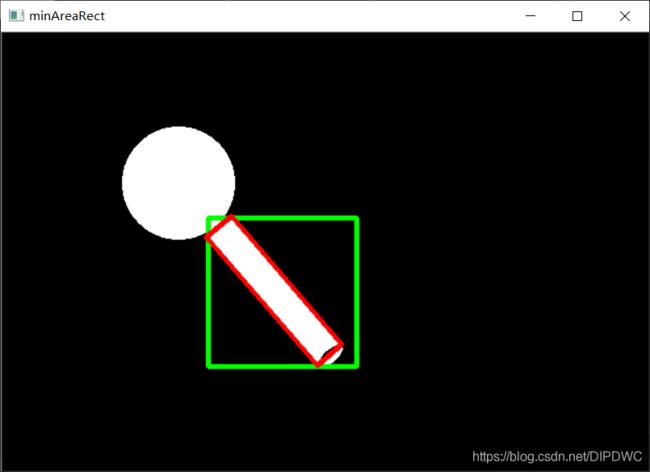
2.8 最小外接圆

接下来，使用函数cv.minEnclosingCircle()查找对象的圆周，它是一个以最小面积完全覆盖物体的圆。

(x,y),radius = cv.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
cv.circle(img,center,radius,(0,255,0),3)

2.8代码：

import numpy as np
import cv2 as cv

img = cv.imread('./data/boundingRect.png')
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggray, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cnt = contours[1]
# 最小外接圆
(x, y), radius = cv.minEnclosingCircle(cnt)
center = (int(x), int(y))
radius = int(radius)
img_minEnclosingCircle = cv.circle(img, center, radius, (0, 255, 0), 3)
cv.imshow('minEnclosingCircle', img_minEnclosingCircle)
cv.waitKey()
cv.destroyAllWindows()

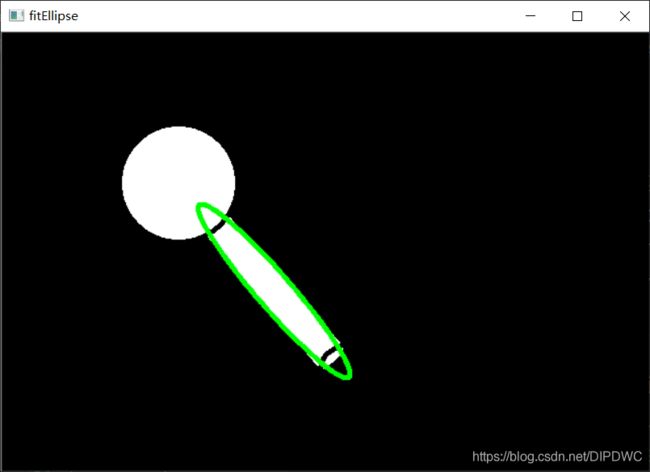
2.9 椭圆拟合

接下来是把一个椭圆拟合到一个对象上，它返回内接椭圆的旋转矩形。

ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),3)

2.9代码：

import numpy as np
import cv2 as cv

img = cv.imread('./data/boundingRect.png')
imggary = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggary, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cnt = contours[1]
# 椭圆拟合
ellipse = cv.fitEllipse(cnt)
img_fitEllipse = cv.ellipse(img, ellipse, (0, 255, 0), 3)
cv.imshow('fitEllipse', img_fitEllipse)
cv.waitKey()
cv.destroyAllWindows()

2.10 直线拟合

同样，我们可以将一条直线拟合到一组点上，下图包含一组白点，我们可以近似一条直线。

rows,cols = img.shape[:2] [vx,vy,x,y] = cv.fitLine(cnt, cv.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv.line(img,(cols-1,righty),(0,lefty),(0,255,0),3)

代码2.10：

import numpy as py
import cv2 as cv

img = cv.imread('./data/boundingRect.png')
imggray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(imggray, 127, 255, cv.THRESH_OTSU)
img2, contours, hierarchy = cv.findContours(imggray, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
cnt = contours[1]
# 直线拟合
rows, cols = img.shape[:2]
[vx, vy, x, y] = cv.fitLine(cnt, cv.DIST_L12, 0, 0.01, 0.01)
leftty = int((-x*vy/vx)+y)
righty = int(((cols-x)*vy/vx)+y)
img_fitLine = cv.line(img, (cols-1, righty), (0, leftty), (0, 255, 0), 3)
cv.imshow('fitLine', img_fitLine)
cv.waitKey()
cv.destroyAllWindows()

3. 结语

图像轮廓是图像处理板块中比较多且比较重要的内容，本篇文章主要是图像轮廓及其特征部分，今天的内容暂时写到这里了，后期小编还会更新轮廓属性部分，如果文章对你有帮助，希望您一键三连哦~~