Tensorflow笔记--基础部分

相关说明：

• 本文是基于北京大学曹健老师的Tensorflow课程摘录的部分笔记，仅供自己学习使用，欢迎各位大佬留言评论交流。
• 视频环境篇：python3.7+tensorflow2.2.0
• 我的环境：python3.8.3+tensorflow(已安装2.3.1，且通过多种方式安装但不成功且不能import)
• 需要添加安装的：英伟达的SDK 10.1版本cudatoolkit=10.1/英伟达深度学习软件包cudnn=7.6
• 集成开发环境：pycharm

第一讲 神经网络计算过程

1.1人工智能三学派

1.行为主义（感知控制论）

2.符号主义（算术逻辑）

3.联结主义（仿生学，神经元连接–计算机具有感性思维）（主流）

准备数据（特征标签对）–>搭建网络–>优化参数–>应用网络（前向传播输出概率值）

1.2Iris花的分类

1.方法

​ 神经网络（特征标签模型）/专家系统（if）

2.MP模型

​ 输入乘以权重求和，通过非线性函数求和输出。

​
$$y=x\ast w+b$$
3.全连接网络

​ 全连接关系（完全二部图）

4.前向传播

​ 经过MP涉及的公式进行计算，注意：此时由于初始化的w和b都是随机产生的

5.损失函数

​ 预测值y与标准答案y_的差距。但损失函数最小时，参数w、b会出现最优值

6.均方误差

​
$$MSE(y,y’)=1/n\Sigma (y-y’)²$$
7.梯度下降

​ ①目的：想要找到一组w,b使得损失函数最小

​ ②梯度：损失函数对各参数求偏导后的向量，函数梯度下降的方向即函数减小方向。

​ ③梯度下降法：沿损失函数梯度下降的方向，寻找损失函数的最小值，得到最优参数的方法。

8.反向传播

​ 从后向前，逐层求损失函数对每层神经元参数的偏导数，迭代更新所有参数

1.3张量生成

1.tensor张量

​ 可以表示0阶到n阶数组（列表） 阶：张量维数

​ 例如：标量（0阶）–向量（1阶）–矩阵（2阶）–张量（n阶）

2.如何创建一个张量

tf.constant(张量内容，dtype=数据类型（可选）)

​ 直接打印包含的信息：数字信息、形状（阶数用”，“隔开）、dtype数据类型

3.特殊张量的创建

​ ①全为0：

tf.zero(维度)

​ ②全为1：

tf.ones(维度)

​ ③全为指定值：

tf.fill(维度，指定值)

​ ④生成正态分布的随机数（默认均值为0，标准差为1）：

tf.random.normal(维度，mean=均值，stddev=标准差)

​ ⑤生成截断式的正态分布函数的随机数

tf.random.truncated_normal(维度，mean=均值，stddev=标准差)

保证生成的数据取值在两倍标准差之内

​ ⑥生成均匀分布的随机数：

tf.random.uniform(维度，minval=最小值，max=最大值)

1.4常用函数

1.强制tensor转化为该数据类型

tf.cast(张量名,dtype=数据类型)

2.计算张量维度上元素的最小值与最大值

tf.reduce_min(张量名)
tf.reduce_max(张量名)

3.axis函数

在一个二维张量或数组中，通过调整axis等于0或1控制执行维度

axis=0代表跨行(down)，axis=1代表跨列(across)

例如：

tf.reduce_mean(张量名，axis=操作轴)#计算张量沿着指定维度的平均值

tf.reduce_sum(张量名，axis=操作轴)#计算张量沿着指定维度的和

4.tf.Varible(初始值)

定义：将变量标记为可训练，被标记的变量会在反向传播中。神经网络中，常用该函数标记待训练参数

5.四则运算

tf.add(张量1,张量2)#加
tf.subtract(张量1,张量2)#减
tf.multiply(张量1,张量2)#乘
tf.divide(张量1,张量2)#除
tf.square(张量名)#平方
tf.pow(张量名,n次方数)#计算某个张量的n次方
tf.sqrt(张量名)#计算某个张量的开方
tf.matmul(矩阵1,矩阵2)#实现两个矩阵的相乘

说明：维度相同才能四则运算

6.特征标签配对函数

tf.data.Dataset.from_tensor_slices((feature,labels))#特征标签配对

7.梯度计算函数

with tf.GradientTape() as tape:
	#若干计算过程
grad=tape.gradient(函数,对谁求导)

8.枚举函数

定义：内建函数，可以遍历每个元素，索引+元素，常在for循环中使用

enumerate(列表名)

9.独热编码

在分类问题中使用：标记类别–1表示真0表示假

tf.one_hot(待转换数据,depth=几分类)

10.softmax函数

前向传播输出y后，用softmax使输出符合概率分布

tf.nn.softmax(x)#使输出符合概率分布

11.assign_sub函数

赋值操作，更新参数的值并返回

w.assign_sub(w要自减的内容)

12.tf.argmax函数

返回张量沿指定维度最大的索引

tf.argmax(张量名,axis=操作轴)

1.5神经网络实现鸢尾花分类实例

1.步骤：

​ 准备数据

​ 数据集读入

​ 数据集乱序

​ 生成训练集和测试集(即x_train/y_train, x_test/y_test)无交集

​ 配成特征标签对，每次读入一部分

​ 搭建网络

​ 定义神经网络中的所有可训练参数

​ 参数优化

​ 嵌套循环迭代，with结构更新参数，显示当前loss

​ 测试数据

​ 计算当前参数前向传播后的准确率，显示当前acc

​ acc/loss可视化

2.代码

#导入相关包
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
#导入数据集
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
#随机打乱数据，seed随机数种子
np.random.seed(116)
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
#将打乱顺序后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train=x_data[:-30]
y_train=y_data[:-30]
x_test=x_data[-30:]
y_train=y_data[-30:]
#转化x的数据类型
x_train = tf.cast(x_train,tf.float32)
x_test = tf.cast(x_test,tf.float32)
#from_tensor_slices函数使输入特征和标签值对应
train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test)).batch(32)
#生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为三分类，故输出层为3个神经元
#用tf.Variable()标记参数可训练
#使用seed使每次生成的随机数相同
w1 = tf.Variable(tf.random.truncated_normal([4,3],stddev=0.1,seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3],stddev=0.1,seed=1))

lr=0.1 #学习率为0.1
train_loss_result = [] #将每轮的loss记录在此列表中，为后续画曲线提供数据
test_acc = [] #将每轮的acc记录在表中，为后续画曲线提供数据
#----------------------------------------------------------------------------
#训练部分
for epoch in range(epoch): #数据集级别的循环，每个epoch循环一次数据集
    for step,(x_train,y_train)in enumerate(train_db):
        with tf.GradientTape() as tape:
            y = tf.matmul(x_train,w1) + b1
            y = tf.nn.softmax(y)
            y_ = tf.one_hot(y_train,depth = 3)
            loss = tf.reduce_mean(tf.square(y_-y))
            loss_all += loss.numpy()
        #计算loss对各个参数的梯度
        grads = tape.gradient(loss,[w1,b1])
        #实现参数更新
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])
    #每个epoch打印loss信息
    print("Epoch {},loss: {}".format(epoch,loss_all/4))
    train_loss_results.append(loss_all / 4)
    loss_all = 0
    #测试部分,total_correct为预测对的样本个数，total_number为测试的总样本个数
    total_correct,total_number = 0,0
    for x_test,y_test in test_db:
        #使用更新后的进行预测
        y = tf.matmul(x_test,w1)+b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y,axis=1)
        #将pred转换为y_test的数据类型
        pred = tf.cast(pred,dtype=y.test.dtype)
        #若分类正确，则correct为1
        correct = tf.cast(tf.equal(pred,y_test),dtype=tf.int32)
        #将每个分支的值加起来
        correct = tf.reduce_sum(correct)
        #将所有batch中的correct数加起来
        total_correct += int(correct)
        #total_number为测试的总样本数，也就是x_test的行数
        total_number += x_test.shape[0]
    acc = total_correct total_number
    test_acc.append(acc)
    print("Test_acc:",acc)
    print("-------------------------------------")
        
#绘制曲线loss
plt.title('Loss Function Curve')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(train_loss_results,label="$Loss")
plt.legend()
plt.show()
#绘制曲线Accuracy
plt.title('Acc Curve')
plt.xlabel('Epoch')
plt.ylabel('Acc')
plt.plot(test_acc,,label="$Accuracy")
plt.legend()
plt.show()

第二讲 神经网络的优化方法

2.1预备知识

1.tf.where(条件语句,真返回A,假返回B)

2.np.random.RandomState.rand(维度)默认为0

​ 返回一个0~1之间的随机数

3.np.vstack(数组1，数组2)

​ 将两个数组按照垂直方向叠加

4.生成网格坐标点的一组函数

​ np.mgrid[起始值：结束值：步长,起始值：结束值：步长,……]#返回若干个维度相同的等差数组

​ x.ravel()#将x变为一维数组，“把.前的值给拉直了”

​ np.c[数组1,数组2,…]#使返回的间隔数值点配对

2.2复杂度与学习率

1.空间复杂度：

​ 层数=隐藏层的层数+1个输出层

​ 总参数=总w+总b

2.时间复杂度

​ 乘加运算次数（权重线）

3.学习率
$$wt+1=wt-lr\ast dloss/dwt(求的是偏导)$$
指数衰减学习率：先用较大的学习率，快速得到最优解，然后逐渐减小学习率，使模型在训练后期稳定

定义式：指数衰减学习率=初始学习率*学习率衰减率^(当前轮数/多少轮衰减一次)

2.3激活函数（暂时不太明白用来干嘛）

1.sigmoid函数
$$f(x)=1/(1+e^{-}x)$$

tf.nn.sigmoid(x)

特点：①易造成梯度消失；②输出非0均值，收敛慢；③幂运算复杂，训练时间长

近几年使用变少

2.Tanh函数
$$f(x)=(1-e^{-}2x)/(1+e^{-}2x)$$

tf.math.tanh(x)

特点：①输出是0均值；②易造成梯度消失；③幂运算复杂，训练时间长

3.Relu函数
$$f(x)=max(x,0)$$

tf.nn.relu(x)

优点：①正区间解决了梯度消失问题；②只需要判断输入是否大于0，计算速度快；③收敛速度远快于前面二者

缺点：①输出非0均值，收敛慢；②Dead RelU问题：某些神经元可能永远不会被激活，导致相应的参数永远不能被更新

4.Leaky Relu函数
$$f(x)=max(ax,x)$$

tf.nn.leaky_relu(x)

5.激活函数总结

​ ①首选relu激活函数

​ ②学习率设置较小值

​ ③输入特征标准化，输入特征满足0为均值，1为标准差正态分布

​ ④初始参数中心化，即让随机生成的参数满足以0为均值，(2/当前层输入特征个数)^0.5为标准差的正态分布

2.4损失函数

1.定义：预测值与已知答案的差距

2.nn优化目标：loss最小

3.均方误差

MSE–方差

loss_mse=tf.reduce_mean(tf.square(y'-y))

4.自定义损失函数

5.交叉熵损失函数CE

表征两个概率分布之间的距离
$$H(y^{\prime },y)=-\Sigma y^{\prime }\ast lny$$

tf.losses.categorical_crossentropy(y',y)

6.总结

一般是将softmax（概率分布）与交叉熵结合

2.5欠拟合与过拟合（泛化性弱）

1.解决方案

欠拟合：增加输入特征项、增加网络参数、减少正则化参数

过拟合：数据清洗、增大数据集、采用正则化、增大正则化参数

2.正则化缓解过拟合

正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据的噪声

L1正则化（减少参数数量，降低复杂度）与L2正则化（减小参数数值降低复杂度）

2.6优化器

定义：引导神经网络更新参数

1.SGD1阶

2.SGDM1阶

3.Adgrad2阶

4.RMSProp2阶

5.Adam结合1、2阶

第三讲 神经网络搭建八股

tf.keras搭建网络八股

3.1搭建网络八股Sequential

1.搭建六步法：

import相关模块->

告知train,test集->

model=tf.keras.models.Sequential搭建网络结构走一遍前向传播->

model.compile训练方法：优化器optimizer、损失函数loss、评测指标metrics->

model.fit训练集的输入特征，训练集的标签->

model.summary打印网络结构

2.Sequential封装的容器

①拉直层

②全连接层

③卷积层

④LSTM层

3.鸢尾花分类实践（改写）

#1.import
import tensorflow as tf
from sklearn import datasets
import numpy as np
#2.train test
x_train = datasets.load_iris().data
y_train = datasets.load_iris().target

np.random.seed(116)
np.random.shuffle(x_train)
np.random.seed(116)
np.random.shuffle(y_train)
np.random.set_seed(116)
#3.model.Sequential
model = tf.keras.models.Sequential([tf.keras.layers.Dense(3,activation='softmax',kernel_regularizer=tf.keras.regularizers.12())])
#4.model.compile
model.compile(optimizer=tf.keras.optimizer.SGD(lr=0.1),loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),metrics=['sparse_categorical_accuracy'])
#5.model.fit
model.fit(x_train,y_train,batch_size=32,epoches=500,validation_split=0.2,validation_freq=20)
#6.model.summary()
model.summary()

3.2搭建网络八股class

1.六步法

修改第三步为：class MyModel(Model) model=MyModel

2.鸢尾花分类（用类改写）

#1.import
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras import Model
from sklearn import datasets
import numpy as np
#2.train test
x_train = datasets.load_iris().data
y_train = datasets.load_iris().target

np.random.seed(116)
np.random.shuffle(x_train)
np.random.seed(116)
np.random.shuffle(y_train)
np.random.set_seed(116)
#3.class MyModel
class IrisModel(Model):
    def __init__(self):
        super(IrisModel,self).__init__()
        self.d1 = Dense(3,activation='segmoid',kernel_regularizer=tf.keras.regularisers.12())
        
    def call(self,x):
        y = self.d1(x)
        return y
model = IrisModel()
#4.model.compile
model.compile(optimizer=tf.keras.optimizer.SGD(lr=0.1),loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),metrics=['sparse_categorical_accuracy'])
#5.model.fit
model.fit(x_train,y_train,batch_size=32,epoches=500,validation_split=0.2,validation_freq=20)
#6.model.summary()
model.summary()

3.3MNIST数据集（手写数字）

1.用Sequential实现手写识别代码

#1.import
import tensorflow as tf
#2.train test
mnist = tf.keras.datasets.mnist
(x_train,y_train), (x_test,y_test)=mnist.load_data()
x_train,x_test = x_train/255.0,x_test/255.0

#3.model.Sequential
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),tf.keras.layers.Dense(128,activation='relu'),tf.keras.layers.Dense(10,activation='softmax')])
#4.model.compile
model.compile(optimizer='adam',loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),metrics=['sparse_categorical_accuracy'])
#5.model.fit
model.fit(x_train,y_train,batch_size=32,epoches=5,validation_data=(x_test,y_test),validation_freq=1)
#6.model.summary()
model.summary()

2.用类实现手写数字识别代码

#1.import
import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras import Model
#2.train test
mnist = tf.keras.datasets.mnist
(x_train,y_train), (x_test,y_test)=mnist.load_data()
x_train,x_test = x_train/255.0,x_test/255.0

#3.class MyModel
class MnistModel(Model):
    def __init__(self):
        super(MnistModel,self).__init__()
        self.flatten = Flatten()
        self.d1 = Dense(128,activation='relu')
        self.d2 = Dense(10,activation='softmax')
        
    def call(self,x):
        x = self.flatten(x)
        x = self.d1(x)
        y = self.d2(x)
        return y
model = MnistModel()
#4.model.compile
model.compile(optimizer='adam',loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),metrics=['sparse_categorical_accuracy'])
#5.model.fit
model.fit(x_train,y_train,batch_size=32,epoches=5,validation_data=(x_test,y_test),validation_freq=1)
#6.model.summary()
model.summary()

3.4FASHION数据集（服装鞋子）

举一反三改写代码

第四讲 神经网络八股扩展

4.1搭建网络八股总览

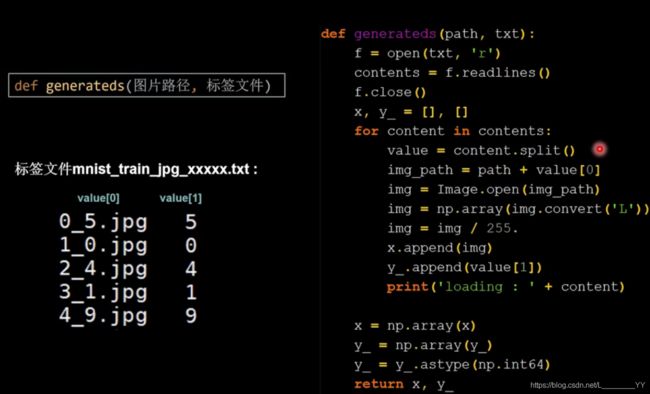
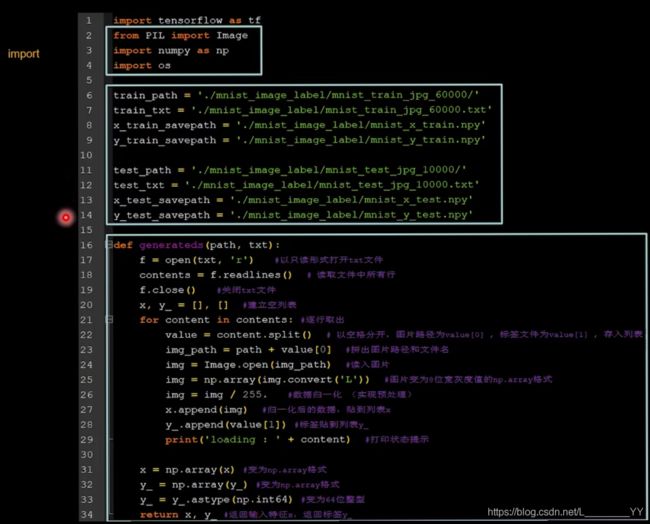
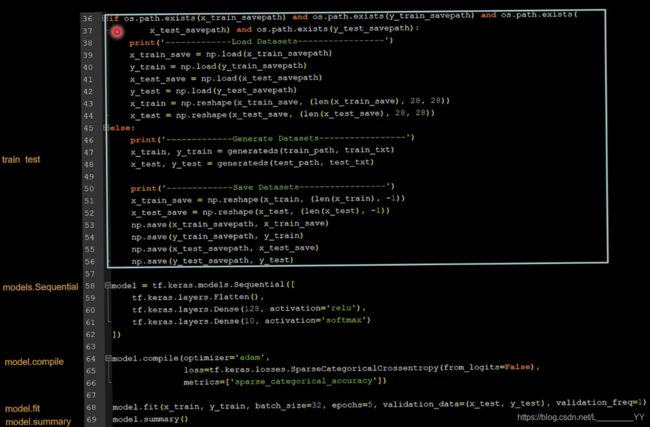
4.2自制数据集

1.自制数据集函数

2.自制数据集引入手写数字完整代码

4.3数据集增强（扩充数据集）

增加泛化性

4.4断点续训（读取保存模型）

1.读取模型：load_weights(路径文件名)

2.保存模型：

tf.keras.callbacks.ModelCheckpoint(
filepath=路径文件名，
save_weights_only=True/False,
save_best_only=True/False)
history=model.fit(callbacks=[cp_callback])

3.断点续训代码

4.5参数提取（把参数存入文本txt）

1.提取可训练参数

model.trainable_variables返回模型中可训练的参数

2.设置print输出格式

np.set_printoptions(threshold=超过多少省略显示)

3.参数提取代码

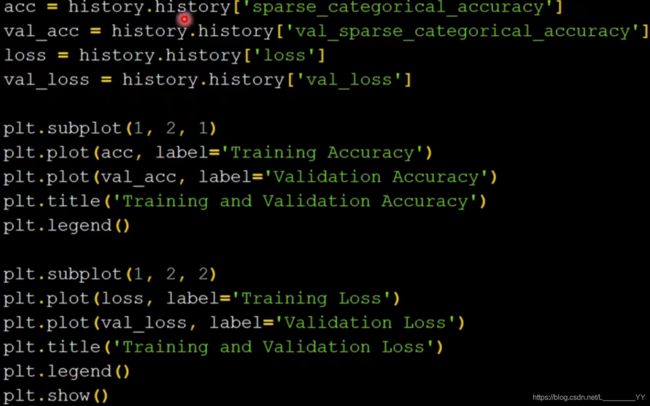
4.6acc/loss可视化，查看训练效果

显示相关曲线

4.7给图识物

1.predict(输入特征，batch_size=整数)

返回前向传播的计算结果

第一步：复现模型（前向传播搭建网络）

第二步：加载参数

第三步：预测结果

2.数字识别代码

第五讲 卷积神经网络

5.1卷积计算过程

1.卷积计算

可以认为是一种有效提取图像特征的方法

输入特征图的channel数，决定了当前层卷积核的深度

2.尺寸

3 * 3 * 1

3 * 3 *3

5 * 5 * 3

5.2感受野

1.感受野

卷积神经网络各输出特征图中的每个像素点，在【原始输入图片】上映射图片大小

5.3全零填充

1.全0填充Padding

padding输出图片长：

• SAME（全0填充）输入长/步长（向上取整）

• VALID（不全0填充）入长-核长+1/步长（向上取整）

5.4TF描述卷积计算层

1.TF描述卷积层框架

tf.keras.layers.Conv2D(

filters = 卷积核个数,

kernel_size = 卷积核尺寸,#正方形写核长整数

strides = 滑动步长,#默认1

padding = "same"or"valid",#默认valid

activation = "relu"or"sigmoid"or"tanh"or"softmax"等，#如有BN可不写

input_shape = (高,宽,通道数)#输入特征图维度

)

5.5批标准化(BN)

1.标准化

是数据符合0均值，1标准差的分布

2.批标准化

是对一小批数据做标准化处理

3.引入可训练参数

γ：缩放因子

β：偏移因子

把BN层加入到卷积层和激活层之间

5.6池化

1.定义

用于减少特征数据量

最大池化可提取图片纹理，均值池化可以保留背景特征

2.TF描述池化

#最大池化：
tf.keras.layers.MaxPool2D(
pool_size=池化核尺寸,#正方形写核长整数
strides=池化步长,#步长整数
padding='valid'or'same'
)
#平均池化：
tf.keras.layers.AveragePooling2D(
pool_size=池化核尺寸,#正方形写核长整数
strides=池化步长,#步长整数
padding='valid'or'same'
)

5.7舍弃（dropout）

1.定义：

在神经网络中，将一部分神经元按照一定概率从神经网络中暂时舍弃。神经网络使用时，被舍弃的神经元恢复链接

2.目的

防止过拟合

3.舍弃框架

tf.keras.layers.Dropout(舍弃的概率)

model = tf.keras.model.Sequential([

	Conv2D(filters=6,kernel_size=(5,5),padding='same'),#卷积层

	BatchNormalization(),#BN层

	Activation('relu'),#激活层

	MaxPool2D(pool_size=(2,2),strides=2,padding='same'),#最大池化

	Dropout(0.2)#dropout层随即舍弃20％神经元

])

5.8卷积神经网络（小结）

1.卷积神经网络的主要模块

特征提取【卷积（convolutional）–>批标准化（BN）–>激活（Activation）–>池化（Pooling）】–>全连接（FC）

2.卷积

特征提取器，CBAPD

3.搭建实例

5.9CIFAR10数据集

RGB三通道，可于官网下载

5.10卷积神经网络搭建实例

CBAPD+六步法

代码：