【图神经网络】简化 GCN(SGC)
本文为图神经网络学习笔记,讲解 SGC。欢迎在评论区与我交流
前言
本教程讲解如何使用 Tensorflow 构建 GCN 的变体 SGC 模型进行节点分类任务。
SGC 简介
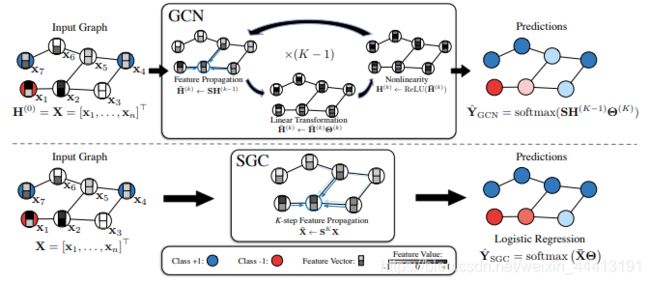
SGC 通过消除 GCN 层间的非线性,将非线性的 GCN 转变为简单的线性模型,减小了模型复杂度 ,在很多任务上比 GCN 以及其他 GNN 模型更加高效。
GCN 做节点分类时:
- 对邻接矩阵归一化并添加自环: S = D − 0.5 A ^ D − 0.5 S=D^{-0.5}\hat{A}D^{-0.5} S=D−0.5A^D−0.5
- 对输入节点特征进行平滑处理: H k = S H k − 1 = D − 0.5 A ^ D − 0.5 H k − 1 H^k=SH^{k-1}=D^{-0.5}\hat{A}D^{-0.5}H^{k-1} Hk=SHk−1=D−0.5A^D−0.5Hk−1
- 对节点特征进行非线性变换: H ^ k = σ ( H k θ k ) = σ ( D − 0.5 A ^ D − 0.5 H k − 1 θ k ) = σ ( D − 0.5 A ^ D − 0.5 H k − 1 W k ) \hat{H}^k=\sigma(H^k\theta^k)=\sigma(D^{-0.5}\hat{A}D^{-0.5}H^{k-1}\theta^k)=\sigma(D^{-0.5}\hat{A}D^{-0.5}H^{k-1}W^k) H^k=σ(Hkθk)=σ(D−0.5A^D−0.5Hk−1θk)=σ(D−0.5A^D−0.5Hk−1Wk)
所以对于节点分类任务,一个 k k k 层的 GCN 可以表示为: Y = s o f t m a x ( S H k − 1 W k ) Y=softmax(SH^{k-1}W^k) Y=softmax(SHk−1Wk)
SGC 移除了 GCN 层间的激活函数,将原先的非线性变换简化为线性变换,因此 SGC 在做节点分类任务时:
- 对邻接矩阵归一化并添加自环: S = D − 0.5 A ^ D − 0.5 S=D^{-0.5}\hat{A}D^{-0.5} S=D−0.5A^D−0.5
- 对输入节点特征进行平滑处理: H k = S H k − 1 = D − 0.5 A ^ D − 0.5 H k − 1 H^k=SH^{k-1}=D^{-0.5}\hat{A}D^{-0.5}H^{k-1} Hk=SHk−1=D−0.5A^D−0.5Hk−1
- 对节点特征进行线性转换: H ^ k = H k θ k = S H k − 1 θ k = S S H k − 2 θ k − 1 θ k = S S θ 1 ⋯ θ k \hat{H}^k=H^k\theta^k=SH^{k-1}\theta^k=SSH^{k-2}\theta^{k-1}\theta^k=SS\theta^1\cdots\theta^k H^k=Hkθk=SHk−1θk=SSHk−2θk−1θk=SSθ1⋯θk
对于节点分类任务,一个 k k k 层的 SGC 可以表示为 Y = s o f t m a x ( S S ⋯ X θ 1 ⋯ θ k ) Y=softmax(SS\cdots X\theta^1\cdots\theta^k) Y=softmax(SS⋯Xθ1⋯θk),简写为:
Y = s o f t m a x ( S k X θ ) = s o f t m a x ( S k X W ) Y=softmax(S^kX\theta)=softmax(S^kXW) Y=softmax(SkXθ)=softmax(SkXW)
SGC中的 S k S^k Sk 可以提前计算,大大减少了计算量。
实践
接下来基于 tf_geometric 实现 SGC 模型。
SGC 实现
对图的邻接矩阵进行对称归一化处理:
updated_edge_index, normed_edge_weight = gcn_norm_edge(edge_index, x.shape[0], edge_weight,renorm, improved, cache)
计算 S k X S^kX SkX,扩大模型的感受野,``aggregator_neighbor聚合一阶邻居节点信息,迭代聚合k` 次,相当于聚合了距离中心节点 k-hop 的邻域信息。
h = x
for _ in range(K):
h = aggregate_neighbors(
h,
updated_edge_index,
normed_edge_weight,
gcn_mapper,
sum_reducer,
identity_updater
)
对上面的聚合结果进行线性变换,即计算 S k X W S^kXW SkXW,然后返回计算结果:
h = h @ kernel
if bias is not None:
h += bias
return h
现在只需要在模型最后一行的输出上添加 softmax 激活函数就可以进行节点分类了。
模型构建
导入相关库。使用 tf_geometric 进行图数据导入、图数据预处理及神经网络的构建。SGC 的具体实现已经在上面详细介绍,后面会使用 keras.metrics.Accuracy 评估模型性能.
# coding=utf-8
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
import tensorflow as tf
from tensorflow import keras
from tf_geometric.layers.conv.sgc import SGC
from tf_geometric.datasets.cora import CoraDataset
使用 tf_geometric 自带的图结构数据接口加载 Cora 数据集:
# 加载 Cora 数据集
graph, (train_index, valid_index, test_index) = CoraDataset().load_data()
定义模型:
model = SGC(num_classes, k=2)
SGC 训练
模型的训练与其他基于 Tensorflow 框架的模型训练基本一致,主要步骤有定义优化器、计算误差与梯度、反向传播等。SGC 模型 K 阶的计算结果由 softmax 映射到 (0,1) 直接进行多分类任务。
# 定义优化器
optimizer = tf.keras.optimizers.Adam(learning_rate=0.2)
for step in range(1,101):
with tf.GradientTape() as tape:
# 前向传播
logits = model([graph.x, graph.edge_index, graph.edge_weight], cache=graph.cache)
logits = tf.nn.log_softmax(logits,axis=1)
# 计算损失
loss = compute_loss(logits, train_index, tape.watched_variables())
vars = tape.watched_variables()
grads = tape.gradient(loss, vars) # 计算梯度
optimizer.apply_gradients(zip(grads, vars)) # 梯度下降优化
valid_acc = evaluate(valid_index) # 计算验证集
test_acc = evaluate(test_index) # 计算测试集
print("step = {}\tloss = {}\tvalid_acc = {}\ttest_acc = {}".format(step, loss, valid_acc, test_acc))
计算损失方法与【ChebyNet】中相同。
用交叉熵损失函数计算模型损失。注意在加载 Cora 数据集时,返回值是整个图数据以及相应的 train_index、valid_index、test_index。TAGCN 在训练时输入整个Graph,计算损失时通过 train_index 计算模型在训练集上的迭代损失。因此,此时传入的 mask_index 是 train_index。由于是多分类任务,需要将节点的标签转换为 one-hot 向量以便与模型输出的结果维度对应。由于图神经模型在小数据集上很容易过拟合,所以这里用 L 2 L_2 L2 正则化缓解过拟合:
def compute_loss(logits, mask_index, vars):
masked_logits = tf.gather(logits, mask_index) # 前向传播(预测)的结果,取训练数据部分
masked_labels = tf.gather(graph.y, mask_index) # 真是结果,取训练数据部分
losses = tf.nn.softmax_cross_entropy_with_logits(
logits=masked_logits, # 预测结果
labels=tf.one_hot(masked_labels, depth=num_classes) # 真实结果,即标签
)
# 用 L2 正则化缓解过拟合
kernel_vals = [var for var in vars if "kernel" in var.name]
l2_losses = [tf.nn.l2_loss(kernel_var) for kernel_var in kernel_vals]
# reduce_mean 计算张量的平均值;tf.add_n 列表对应元素相加
return tf.reduce_mean(losses) + tf.add_n(l2_losses) * 5e-5
SGC 评估
评估方法与【ChebyNet】中相同。
评估模型性能时只需传入 valid_mask 或 test_mask,通过 tf.gather 函数可以拿出验证集或测试集在模型上的预测结果与真实标签,用 keras自带的 keras.metrics.Accuracy 计算准确率:
def evaluate(mask):
logits = forward(graph # 前向传播结果
logits = tf.nn.log_softmax(logits, axis=1) # 假设函数处理
masked_logits = tf.gather(logits, mask) # 预测结果
masked_labels = tf.gather(graph.y, mask) # 真实标签
# 返回预测结果向量最大值的索引
y_pred = tf.argmax(masked_logits, axis=-1, output_type=tf.int32)
accuracy_m = keras.metrics.Accuracy()
accuracy_m.update_state(masked_labels, y_pred)
return accuracy_m.result().numpy() # 准确度结果转换为 numpy 返回
运行结果
step = 1 loss = 1.9458770751953125 valid_acc = 0.5120000243186951 test_acc = 0.5389999747276306
step = 2 loss = 1.8324840068817139 valid_acc = 0.722000002861023 test_acc = 0.7350000143051147
step = 3 loss = 1.7052000761032104 valid_acc = 0.4740000069141388 test_acc = 0.4729999899864197
step = 4 loss = 1.6184687614440918 valid_acc = 0.5580000281333923 test_acc = 0.5360000133514404
...
step = 97 loss = 0.9681359529495239 valid_acc = 0.7919999957084656 test_acc = 0.8130000233650208
step = 98 loss = 0.9678354263305664 valid_acc = 0.7919999957084656 test_acc = 0.8100000023841858
step = 99 loss = 0.9675441384315491 valid_acc = 0.7919999957084656 test_acc = 0.8100000023841858
step = 100 loss = 0.967261791229248 valid_acc = 0.7919999957084656 test_acc = 0.8100000023841858
有帮助的话点个赞加关注吧
完整代码见【demo_sgc.py】,完整教程见【Tensorflow-SGC-Tutorial】。