纹理特征二：GLRLM--灰度行程矩阵

纹理特征二：GLRLM–灰度行程矩阵

1. GLCM 的解释与计算

GLRLM，全程 gray-level run-length matrix，这里翻译为 灰度形成矩阵。
概念描述： 灰度共生矩阵用于描述图像某一像素值$i$沿某一方向$\theta$连续相邻为$j$的个数，记GLRLM中一个值为$D(i,j,\theta )$，其中$i$是像素值或灰度值，$j$是连续相邻数，$\theta$是角度或方向，一般$\theta$的值为$0^o,45^o,90^o,135^o$。
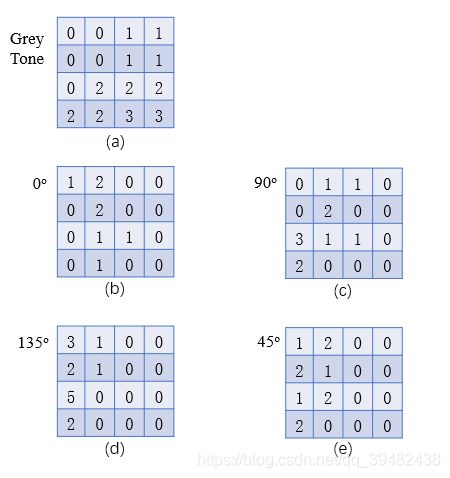
举例说明： 下图图(a)表示一副图像的灰度值，因为$4\times 4$矩阵，故在$0^o$方向上某元素最大连续相邻数只能为4。

• 对于灰度值0，在该方向上，1个0连续相邻的情况为1，2个0连续相邻的情况为2，没有3个和4个0相邻的情况，故0元素的行程向量为 $[1,2,0,0]$ ；
• 对于灰度值1，在该方向上，1个1连续相邻的情况为0，2个1连续相邻的情况为2，3个1相邻的情况为0，4个1连续相邻的情况为0，所以1元素的行程向量为$[0,2,0,0]$;
• 对于灰度值2，在该方向上，1个2连续相邻的情况为0，2个2连续相邻的情况为1，3个2相邻的情况为1，4个2连续相邻的情况为0，所以2元素的行程向量为$[0,1,1,0]$;
• 对于灰度值3，在该方向上，1个3连续相邻的情况为0，2个3连续相邻的情况为2，3个2相邻的情况为0，4个3连续相邻的情况为0，所以3元素的行程向量为$[0,1,1,0]$

所以，在$0^o$方向上的GLRLM为：$$[[1,2,0,0],[0,2,0,0],[0,1,1,0],[0,1,1,0]]$$
$0^o,90^o,135^o,45^o$方向上的GLRLM分别如图(b )，(c )，(d ), (e )所示。

2.GLRLM计算得到的纹理特征

像素值（灰度值）为$i$，连续相邻数$j$，角度值（方向）为$\theta$，$p(i,j|\theta )$为在$\theta$方向上连续$j$ 个$i$值的情况的个数或概率（用频率近似概率）。
则有：
1.Short Run Emphasis(SRE)
$$SRE=\frac{{\sum }_i{\sum }_j[\frac{p(i,j|\theta )}{j^2}]}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

2.Long Run Emphasis(LRE)
$$LRE=\frac{{\sum }_i{\sum }_j{j}^{2}p(i,j|\theta )}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

3.Gray Level Non_Uniformity(GLM)
$$GLM=\frac{{\sum }_i[{\sum }_{j}p(i,j|\theta ){]}^2}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

4.Run Length Non_Uniformity(RLM)
$$RLN=\frac{{\sum }_j[{\sum }_{i}p(i,j|\theta ){]}^2}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

5.Run Percentage(RP)
$$RP=\sum _i\sum _j\frac{p(i,j|\theta )}{N_p}$$
            $N_p$是GLRLM中元素个数

6.Low Gray Level Run Emphasis(LGLRE)
$$LGLRE=\frac{{\sum }_i{\sum }_j[\frac{p(i,j|\theta )}{i^2}]}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

7.High Gray Level Run Emphasis(HGLRE)
$$HGLRE=\frac{{\sum }_i{\sum }_j{i}^{2}p(i,j|\theta )}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$
8.Short Run Low Gray Level Emphasis(SRLGLE)
$$SRLGLE=\frac{{\sum }_i{\sum }_j[\frac{p(i,j|\theta )}{i^2{j}^2}]}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

9.Short Run High Gray Level Emphasis(SRHGLE)
$$SRHGLE=\frac{{\sum }_i{\sum }_j[\frac{i^{2}p(i,j|\theta )}{j^2}]}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$

10.Long Run Low Gray Level Emphasis(LRLGLE)
$$LRLGLE=\frac{{\sum }_i{\sum }_j[\frac{j^{2}p(i,j|\theta )}{i^2}]}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$
11.Long Run High Gray Level Emphasis(LRHGLE)
$$LRHGLE=\frac{{\sum }_i{\sum }_j{i}^2{j}^{2}p(i,j|\theta )}{{\sum }_i{\sum }_{j}p(i,j|\theta )}$$
12.Gray-Level Variance (GLV)

13.Run-Length Variance (RLV)

！建议您同时阅读

《纹理特征一：GLCM—灰度共生矩阵》
《纹理特征三：GLSZM–灰度区域大小矩阵》
《纹理特征四：NGTDM–邻域灰度差矩阵》