灰度共生矩阵(Gray-level Co-occurrence Matrix,GLCM)
1、概念:
(下面这些概念我也不懂,看着就头疼,自行了解,不过应该支持原创!)
1、灰度共生矩阵(GLDM)的统计方法是20世纪70年代初由R.Haralick等人提出的,它是在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下,提出的具有广泛性的纹理分析方法。
2、灰度共生矩阵(Gray-level Co-occurrence Matrix,GLCM),又叫做灰度共现矩阵;
3、个人理解:就是通过统计两个灰阶值在指定的空间分布上出现的频率分布,来熊另外一个角度反映图像的对比对,方差等信息,
2、相关原理
1、The GLCM is calculates how often a pixel The GLCM is calculates how often(频率) a pixel with gray with gray-level (grayscale intensity or level (grayscale intensity or
Tone) value i occurs either horizontally, occurs either horizontally,
vertically, or diagonally to adjacent pixels vertically, or diagonally to adjacent pixels
with the value with the value j .
2、共生矩阵用两个位置的像素的联合概率密度来定义,它不仅反映亮度的分布特征,也反映具有同样亮度或者接近亮度的像素之间的位置分布特性,是有关图像亮度变化的二阶统计特征。它是定义一组纹理特征的基础。
3、由于纹理是由灰度在空间位置上反复出现而形成的,因而在图像空间中像个某距离的两像素之间会存在一定的灰度关系,即图像中灰度的空间相关特性。灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法。
4、像素灰度在空间位置上的反复出现形成图像的纹理,GLCM是描述具有某种空间位置关系两个像素灰度的联合分布;
灰度共生矩阵被定义为从灰度为i的像素点出发,离开某个固定位置(相隔距离为d,方位为)的点上灰度值为的概率,即,所有估计的值可以表示成一个矩阵的形式,以此被称为灰度共生矩阵。对于纹理变化缓慢的图像,其灰度共生矩阵对角线上的数值较大;而对于纹理变化较快的图像,其灰度共生矩阵对角线上的数值较小,对角线两侧的值较大。由于灰度共生矩阵的数据量较大,一般不直接作为区分纹理的特征,而是基于它构建的一些统计量作为纹理分类特征。Haralick曾提出了14种基于灰度共生矩阵计算出来的统计量:即:能量、熵、对比度、均匀性、相关性、方差、和平均、和方差、和熵、差方差、差平均、差熵、相关信息测度以及最大相关系数。
4、矩阵的物理意义
用GLCM表示灰度共生矩阵,它是一个L*L的矩阵(L为灰度级,就是一幅图中包含的不同灰度或者颜色的个数),是具有一定的空间位置关系且灰度分别为i和j的两个像素出现的次数或频率(归一化)
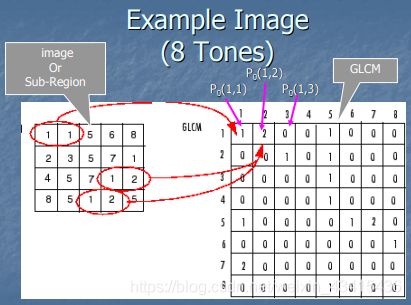
- 8个gray-level(因为左图中最大值灰度值为8),构成的8×8的GLCM,GLCM宫格两边的1-8数据,表示8个灰度级(gray level),对应左图中的数据1-8;
- GLCM表示所有gray-level的组合,比如:
GLCM(1,1)表示左图I中gray-level值为1和1的组合,GLCM(1,1)=1表示该组合有1个相邻的成对点;
GLCM(4,5)表示左图I中gray-level为4和gray-level为5的组合,GLCM(4,5)=1表示该组合有1个相邻的成对点;
GLCM(i,j)表示左图I中gray-level为i和gray-level为j的有多少个相邻的成对点。
(i,表示垂直方向的1-8,j表示水平方向的1-8) - P0中的0表示水平方向,即0°方向,另外还有45°方向、90°方向、135°方向
距离(a,b)的取值不同,灰度共生矩阵中的值不同。a和b的取值要根据纹理周期分布的特征来选择,对于较细的纹理,选取(1,0),(1,1),(2,0)等这样的值是有必要的。a,b取值较小对应于变化缓慢的纹理图像,其灰度共生矩阵对角线上的数值较大。纹理的变化越快,则对角线上的数值越小,而对角线两侧的值增大。
共生矩阵实际上是两个像素点的联合直方图,对于图像中细而规则的纹理,成对像素点的二维直方图倾向于均匀分布;对于粗而规则的纹理,则倾向于最对角分布。
5、gray-level之间的空间位置关系:
Distance between the pixel of interest and its neighbor, specified as a p-by-2 array of integers. Each row in the array is a two-element vector,** [row_offset, col_offset]**, that specifies the relationship, or offset, of a pair of pixels. row_offset is the number of rows between the pixel-of-interest and its neighbor. col_offset is the number of columns between the pixel-of-interest and its neighbor. Because the offset is often expressed as an angle, the following table lists the offset values that specify common angles, given the pixel distance D.


距离差分值(a,b) 取不同的数值组合,可以得到不同情况下的联合概率矩阵。(a,b)取值要根据纹理周期分布的特性来选择,对于较细的纹理,选取(1,0)、(1,1)、(2,0)等小的差分值。
- 当 a=1,b=0 时,像素对是水平的,即0度扫描;
- 当 a=0,b=1 时,像素对是垂直的,即90度扫描;
- 当 a=1,b=1 时,像素对是右对角线的,即45度扫描;
- 当 a=-1,b=-1时,像素对是左对角线,即135度扫描。
所以可以构成四张8*8的GLCM表。
联合概率矩阵是什么?????
6、计算过程
- 取图像(N×N)中任意一点 (x,y)及偏离它的另一点 (x+a,y+b),设该点对的灰度值为(g1,g2)。令点(x,y) 在整个画面上移动,则会得到各种 (g1,g2)值,设灰度值的级数为 k,则(g1,g2) 的组合共有 k^2种。
- 对于整个画面,统计出每一种(g1,g2)值出现的次数,然后排列成一个方阵,在用(g1,g2) 出现的总次数将它们归一化为出现的概率P(g1,g2),这样的方阵称为灰度共生矩阵。
- 距离差分值(a,b) 取不同的数值组合,可以得到不同情况下的联合概率矩阵。(a,b)取值要根据纹理周期分布的特性来选择,对于较细的纹理,选取(1,0)、(1,1)、(2,0)等小的差分值。
- 当 a=1,b=0时,像素对是水平的,即0度扫描;
- 当a=0,b=1 时,像素对是垂直的,即90度扫描;
- 当 a=1,b=1时,像素对是右对角线的,即45度扫描;
- 当 a=-1,b=-1时,像素对是左对角线,即135度扫描。
这样,两个象素灰度级同时发生的概率,就将 (x,y)的空间坐标转化为**“灰度对”** (g1,g2)的描述,形成了灰度共生矩阵。
一幅图象的灰度共生矩阵能反映出图象灰度关于方向、相邻间隔、变化幅度的综合信息,它是分析图象的局部模式和它们排列规则的基础。
例如: 下图是某纹理像素的放大,和对应的像素灰度矩阵

此图像只有三种灰度,故灰度级为3,灰度共生矩阵是一个3*3的矩阵
7、矩阵的特征量
从灰度共生矩阵上可以简单的看出,如果对角附近的元素有较大的值,说明图像的像素具有相似的像素值,如果偏离对角线的元素会有比较大的值,说明像素灰度在局部有较大变化。从共生矩阵导出一些反映矩阵状况的参数,典型的有以下几种:
- 对比度(或反差)(contrast):
纹理沟纹越深,其对比度越大,视觉效果越清晰;反之,对比度小,则沟纹浅,效果模糊。灰度差即对比度大的象素对越多,这个值越大。灰度公生矩阵中远离对角线的元素值越大,con越大。所以con越大图像越清晰。
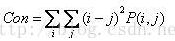
- 相关度(inverse different moment):
度量空间灰度共生矩阵元素在行或列方向上的相似程度,因此,相关值大小反映了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值就大;相反,如果矩阵像元值相差很大则相关值小。 - 能量:
是灰度共生矩阵元素值的平方和,所以也称之为能量,反映了图像灰度分布均匀程度和纹理粗细度。ASM值大表明一种较均一和规则变化的纹理模式。 - 熵(entropy):
熵在物理中的含义就是物体的规则度,越有序熵越小,越无序熵越大。此处熵同样表示图像的信息量,当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有值几乎相等时,共生矩阵中元素分散分布时,熵较大。它表示了图像中纹理的非均匀程度或复杂程度。 - 自相关(correlation):
反应了图像纹理的一致性。如果图像中有水平方向纹理,则水平方向矩阵的COR大于其余矩阵的COR值。

Reference
- https://www.mathworks.com/help/images/ref/graycomatrix.html 参考matlab官方解释
- https://prism.ucalgary.ca/handle/1880/51900
- http://www.dididongdong.com/archives/4327
- https://blog.csdn.net/zhangxz259/article/details/81700167
问题:
1、共生矩阵的空间位置如何设定?
2、如何缩减灰度级,减少计算量(如256灰阶,这将是超级大的计算量)?
如此庞大的矩阵会使后续的计算量增加,所以灰度共生矩阵一般要经过处理以减少灰度级数,比如通过分析纹理图像直方图,在不影响图像纹理质量的前提下,经过适当的变换压缩灰度级。