蓝桥杯python必会算法之贪婪算法
本文主要介绍的是贪婪算法的python实现,并列举了蓝桥杯比赛实例。尽量使用了简单易懂的语言,代码也做了充分的注释,觉得有帮助的小伙伴可以点个赞呀。
1、什么是贪婪算法
顾名思义,贪婪指的是总是做出当前最好的选择,只关注眼前利益,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。虽然看起来比较短视,没有长远眼光,但在某些时候贪婪算法会取得比较好的收益。
要会判断一个问题能否用贪心算法来计算。
(补充说明:动态规划每次都是综合所有问题的子问题的解得到当前的最优解(全局最优解),而不是贪心地选择;回溯法是尝试选择一条路,如果选择错了的话可以“反悔”,也就是回过头来重新选择其他的试试。)
2、贪婪算法举例(蓝桥杯练习题或真题)
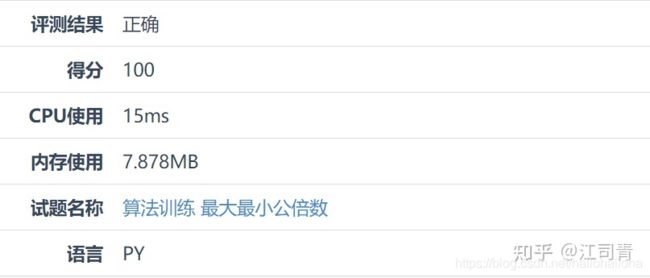
1.算法训练:最大最小公倍数
资源限制 时间限制:1.0s 内存限制:256.0MB
问题描述 已知一个正整数N,问从1~N中任选出三个数,他们的最小公倍数最大可以为多少。
输入格式 输入一个正整数N。
输出格式 输出一个整数,表示你找到的最小公倍数。
样例输入 9 样例输出 504
数据规模与约定 1 <= N <= 106。
问题分析:
这一题在分析的过程中的确是使用贪心算法,由于我要找最大的最小公倍数,所以我每次只需要得到局部的最优解,不断比较,保留大的,舍弃小的值。
但实际这一题的结果非常容易想到,不需要繁琐的过程,详细见代码。
2.算法练习:Huffuman树
资源限制 时间限制:1.0s 内存限制:512.0MB
问题描述 Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。 给出一列数{pi}={p0,
p1, …, pn-1},用这列数构造Huffman树的过程如下:
1. 找到{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。
2. 重复步骤1,直到{pi}中只剩下一个数。 在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。 本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。例如,对于数列{pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
1. 找到{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。
2. 找到{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。
3. 找到{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。
4. 找到{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。
5. 现在,数列中只剩下一个数27,构造过程结束,总费用为5+10+17+27=59。输入格式 输入的第一行包含一个正整数n(n<=100)。 接下来是n个正整数,表示p0, p1, …,
pn-1,每个数不超过1000。输出格式 输出用这些数构造Huffman树的总费用。
样例输入 5 5 3 8 2 9
样例输出 59
问题分析:
本题的字数非常多,但是不难,需要耐心读题。在比赛中遇到题干非常长的题目很正常,一定要细心耐心。
在哈夫曼树的构造过程中,只关注当前最小的两个数,即局部最优解
3.算法练习:完美的代价
资源限制 时间限制:1.0s 内存限制:512.0MB
问题描述
回文串,是一种特殊的字符串,它从左往右读和从右往左读是一样的。小龙龙认为回文串才是完美的。现在给你一个串,它不一定是回文的,请你计算最少的交换次数使得该串变成一个完美的回文串。
交换的定义是:交换两个相邻的字符 例如mamad 第一次交换 ad : mamda 第二次交换 md : madma
第三次交换 ma : madam (回文!完美!)输入格式 第一行是一个整数N,表示接下来的字符串的长度(N <= 8000) 第二行是一个字符串,长度为N.只包含小写字母
输出格式 如果可能,输出最少的交换次数。 否则输出Impossible
样例输入 5 mamad
样例输出 3
问题分析:
关键是要找到贪心策略。对于这一题来说,首先判断这个字符串能不能够经过交换变成完美的回文字符串,满足条件后每一步都使用贪心策略。
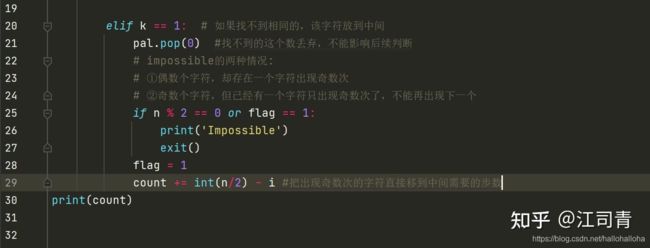
①判断:
若字符串长度为偶数,则每个字符出现的次数都必须是偶数次,否则不对称
若字符串长度为奇数,则只能有一个字符出现奇数次(在字符串最中间出现一次)
判断实现比较简单,注意减少代码复杂度(题给字符串长度范围是8000,python很容易运行超时)
②贪心策略:
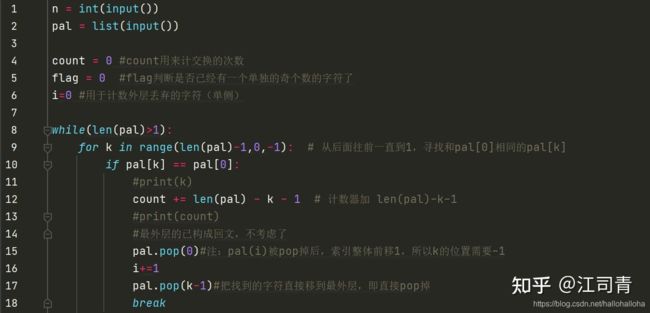
对于偶数长度的字符串,我们从第一个开始遍历,再倒序遍历出同样的,这个倒序遍历出来的序号,就是该移动的步数。 倒序列表需要不断更新,已经构成回文的外层字符不再考虑。
对于奇数的字符串,其实贪心策略和偶数的时候一样,只不过我们一直遍历下去会有一个字符没有匹配,那么这个字符肯定是放在中间的,我们设置一个判断,假如剩余的该字符个数不是1,按照和偶数一样的遍历,如果该字符是1,直接移动到最中间的位置。
详细代码:
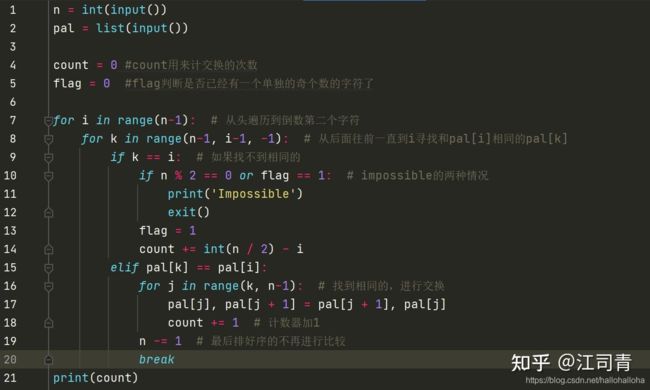
代码出处:
https://blog.csdn.net/qq_31910669/article/details/103641497
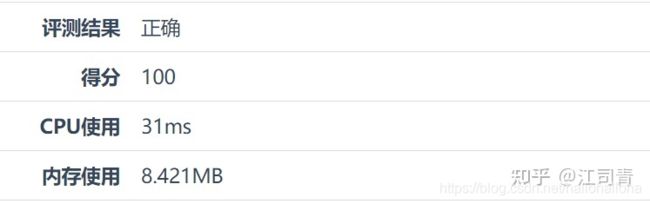
测评结果:
该测评结果有一个测试超时,得分90分
![]()
省时策略:
python中的迭代和交换都要花费大量的时间。
在改进的代码中,对于找到的字符,我不对它进行逐次的交换,而是直接pop掉,利用它的索引找到需要移动的次数。
下一次的遍历针对的即是已经去掉外层字符的新列表,这样迭代下去,列表会越来越短,就达到了省时的目的。
4.真题:翻硬币
资源限制 时间限制:1.0s 内存限制:256.0MB
问题描述 小明正在玩一个“翻硬币”的游戏。 桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零)。
比如,可能情形是:oo*oooo 如果同时翻转左边的两个硬币,则变为:oooo***oooo
现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作,那么要求:输入格式 两行等长的字符串,分别表示初始状态和要达到的目标状态。每行的长度<1000
输出格式 一个整数,表示最小操作步数。
样例输入1
********** oo样例输出1 5
样例输入2
ooo***
ooo***样例输出2 1
问题分析:
运用了贪心的思想,遍历所有硬币只要与当前硬币状态不同我就翻,最多翻n-1次(每次都翻)。