电路考前复习总结

 

目录

一、简算题

1.1等效电阻求法

1.1.1串并联等效

1.1.2“Y”“Δ”联结

1.1.3输入电阻的求法

1.1.4电路定理

1.1.5例题

1.2最大功率传输（含理想变压器）

1.2.1直流通路

1.2.2交流通路

1.2.3补充

1.2.4理想变压器的主要性能

1.2.5例题

1.3特勒根定理、互易定理

1.3.1特勒根定理一

1.3.2特勒根定理二

1.3.3互易定理

1.3.4例题

1.4含有理想运算放大器的电路的分析

1.4.1虚短

1.4.2虚断

1.4.3虚地

1.4.4例题

1.5非正弦周期信号电压、电流有效值及功率求解

​

1.6二端口网络Y、Z参数的计算（含受控源）

1.6.1Y参数

1.6.2Z参数

1.6.3Y矩阵与Z矩阵的关系

1.7串并联谐振

1.7.1串联谐振

1.7.2并联谐振

1.8割集、关联、回路矩阵

1.8.1割集矩阵

1.8.2关联矩阵

1.8.3回路矩阵

二、计算题

2.1含有耦合电感的电路列写方程

2.2一阶电路的时域分析

2.3二瓦计法测功率

2.4拉普拉斯变换求解二阶电路

2.4.1拉普拉斯变换的基本性质

2.4.2拉普拉斯逆变换

2.4.3电路的基本定理的复频域形式

---

一、简算题

1.1等效电阻求法

1.1.1串并联等效

（1）串联：

（2）并联：

         常用：

1.1.2“Y”“Δ”联结

当电路中电阻之间联接关系较复杂时，一种可靠的方法是在图中导线相交之处分别用不同的点描述，通过对原电路进行有效组合与重画，将之变成易识别的联接形式，之后求解等效电阻。

①分别找出电路中的相交点，并用不同的字母标注；

②电路中导线直接联接的点，用同一字母表示；

③按照从左到右的顺序在一条直线上画出各点，依次在每两点之间填入相应的电阻，对原电路进行重画；

④ 利用串、并联公式计算等效电阻

1.1.3输入电阻的求法

（1）等效变换法

利用1.1.1、1.1.2中电阻的变换方法求。

注:当电路中含有受控源时不能用此法。

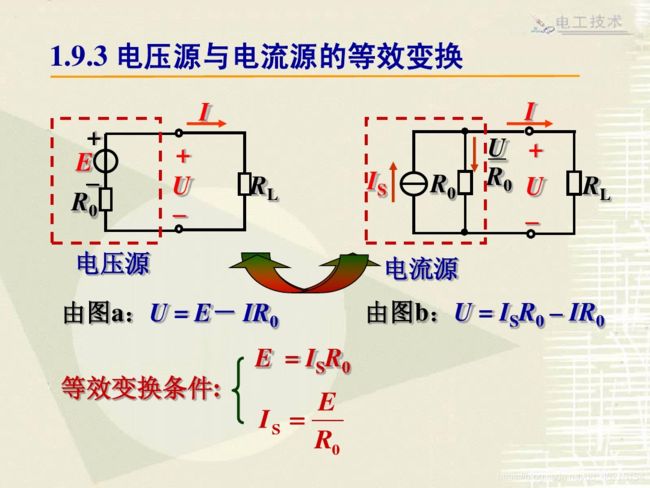
补充：电源的等效变换（注意电流源的方向）

（2）外施激励法

外加电压源，求出端口电流；外加电流源，求出端口电压；电路中独立源置零，受控源不变。通过列写方程找出外加的电压和电流关系即可求出等效电阻。

（3）开路断路法

(分别为端口开路时的电压和短路时的电流，在诺顿等效电路中求解比较简便)

1.1.4电路定理

（1）戴维南定理

一个含独立电源、线性电阻和受控源的一端口,对外电路来说,可以用一个电压源和电阻的串联组合等效置换,此电压源的激励电压等于一端口的开路电压,电阻等于一端口内全部独立电源置零后的输入电阻。

★★★求解戴维南等效电路步骤:

①移去待求支路，使电路成为一个含源的一端口网络。

②求含源一端口网络的开路电压和短路电流。

③求该一端口网络的除源输入电阻。

  Ⅰ对不含受控源的网络，在除源采用电阻的串并联等效，星型三角形等效即可求出输入电阻。

  Ⅱ对含受控源的网络，在除去独立电源后采用外施激励法，然后找出端口电压与端口电流的关系，其输入电阻等于端口电压与端口电流的比值。

  Ⅲ含受控源网络中也可采用开路短路法，在不除源情况下求得含源一端口网络的开路电压和短路电流，其输入电阻等于开路电压与短路电流比值。

  Ⅳ画出对应的等效电源电路，接入所移去的待求支路，求出响应。

▶用戴维宁定理分析电路“一步法”步骤：

①断开负载支路，求端口处的伏安关系式。
②根据伏安关系式画出戴维宁等效电路并接上负载支路，求解各未知量。

（2）诺顿定理

一个含独立电源、线性电阻和受控源的一端口,对外电路来说,可以用一个电流源和电阻的并联组合等效置换,此电流源的激励电流等于一端口的短路电流,电阻等于一端口内全部独立电源置零后的输入电阻。

（3）叠加定理

在线性电阻电路中有几个独立源共同作用时，各支路的电流或电压等于各个独立源单独作用时在该支路的电流或电压的代数和叠加。

使用时应注意：

①叠加定理适用于线性电路，不适用于非线性电路。

②在叠加定理的各分电路中不作用的电压源置零，在电压源处用短路代替，不作用的电流源置零，在电流源处用开路代替，电路中所有电阻都不予变动，受控源仍保留在各分路中。

③叠加时各分路中的电压和电流的参考方向可以取为与原电路相同。取代数和时，应注意各分量前的“+”“-”号。

④原电路的功率不等于按各分电路计算所得功率的叠加，这是因为功率是电压和电流的乘积，与激励不成线性关系。

（4）齐性定理

在线性电路中，当所有激励（电压源和电流源）都同时增大或缩小K倍（K为实常数）时，响应（电压和电流）也将同时增大或缩小K倍。

（5）替代定理

在电路中如已求得与两个一端口网络连接端口的电压u与电流i，那么就可用一个us=u的电压源或一个is=i的电流源来替代其中的一个网络，而使另一个网络的内部电压、电流均维持不变。

注：最大功率传输定理，特勒根定理，互易定理在下面单独总结。

1.1.5例题

例1：求如图所示电路的等效电阻。

解：将电路重画为如下图所示

右边为一个平衡电桥，c,d等电位，可以看做一条导线（短路）。等效电阻为欧

例2：试求如图所示梯形电路中各支路电流，结点电压和。其中Us=10V。

例3：

注：上分式中有负号出现，因此，当存在受控源时，在一定的参数条件下，有可能是零，也有可能是负值，负电阻元件实际是一个发出功率的元件。

1.2最大功率传输（含理想变压器）

1.2.1直流通路

负载电阻与单口网络的输出电阻相等，满足=条件时，称为最大功率匹配，此时负载电阻获得的最大功率为

1.2.2交流通路

工作于正弦稳态的单口网络向一个负载供电，如果该单口网络可用戴维南等效电路（其中,R0>0）代替，则在负载阻抗等于含源单口网络输出阻抗的共轭复数（即电阻成分相等，电抗成分只数值相等而符号相反）时，负载可以获得最大平均功率。这种匹配成为共轭匹配。

1.2.3补充

最大功率传输指的是有功功率。

▶拓展：功率

①视在功率S、有功功率P、无功功率Q三者之间的数量关系，恰好相当于直角三角形的三边关bai系，S相当于斜边，P和Q相当于两条直角边，称为功率三角形。其换算公式如下：S²＝Q²＋P²

②cosΦ=P/S由此可见功率因数cosΦ可以定义为负载消耗的有功功率与其视在功率的比值，它表征了负载消耗的有功功率在视在功率中所占比例。

③三相负荷中，任何时候这三种功率总是同时存在，发动机发的电就要包括这这三种功率：

视在功率S=UI（满足一端口网络电路有功功率）

有功功率P=UIcosΦ（做功发热的功率）

无功功率Q=UIsinΦ（建立磁场输送能量的功率）

④功率因数cosΦ=P/S（有功功率/视在功率）

⑤注意点：

  Ⅰ当负载为纯电阻时，电压与电流相位相同，Φ＝0°，cosΦ＝1，电阻消耗的功率全部是有功功率（P=UI）。

  Ⅱ当负载是纯电感或纯电容时，电压和电流的相位差Φ=90°，cosΦ=0，有功功率P=0，所以纯电感或纯电容负载是不消耗有功功率的。

  Ⅲ无功功率的单位是乏（var）或千乏（Kvar）、兆乏（Mvar）。当负载为纯电感或纯电容时，Φ＝90°,sinΦ＝1,所以Q＝UI，即只有无功功率而不消耗有功。当负载为纯电阻时，Φ＝0°，sinΦ＝0，所以Q＝0，即只消耗有功功率而不需要无功。

  Ⅳ视在功率的单位为伏安（VA），或千伏安（KVA）、兆伏安（MVA）。交流发电设备都是按照规定的电压和电流进行设计和使用的，所以有时用视在功率表示设备的容量是比较方便的，例如变压器的容量就是指它的视在功率。

1.2.4理想变压器的主要性能

（1）变压关系

注意：理想变压器的变压关系与两线圈中电流参考方向的假设无关，但与电压极性的设置有关，若u1、u2的参考方向的“+”极性端一个设在同名端，一个设在异名端，如图3所示，此时u1与u2之比为：

（2）变流关系

注意：理想变压器的变流关系与两线圈上电压参考方向的假设无关，但与电流参考方向的设置有关，若i1、i2的参考方向一个是从同名端流入，一个是从同名端流出，此时i1与i2之比为：

（3）变阻抗关系

（4）功率性质

▶（1）理想变压器既不储能，也不耗能，在电路中只起传递信号和能量的作用。

   （2）理想变压器的特性方程为代数关系，因此它是无记忆的多端元件。

1.2.5例题

 

1.3特勒根定理、互易定理

1.3.1特勒根定理一

对于一个具有n个节点和b条支路的电路，假设各支路电流与电压取关联参考方向，表示为：i1、u1，i2、u2，……，ib、ub，则在任何时刻t，有：

实质是：功率守恒。这是一个普适定理，因此，它适用于一切集总电路，而不管它是线性的、非线性的、时变的、时不变的。

1.3.2特勒根定理二

有两个电路，假设它们的节点数、支路总数相同，图也相同，支路上的元件可以不同。并假定各支路电流和电压取关联参考方向，则两电路对应支路电压和电流的交叉乘积代数和为零：

该定理描述的是两个具有相同拓扑结构的电路，其电压电流之间满足的一个数学关系式，没有具体的物理含义，因此称为“似功率定理”。

1.3.3互易定理

（1）互易定理的第一种形式

对于一个线性电阻电路，单一电压源Us在1－1’支路中作用，而在2－2’支路中产生了电流i2，i2的值等于将电压源Us移到2－2’支路上作用，在1－1’支路中产生的电流i1的值。电流电压方向选关联参考方向。

（2）互易定理的第二种形式

对于一个线性电阻电路，单一电流源is在1－1’支路中作用，而在2－2’支路中产生了电压u2，u2的值等于将电流源is移到2－2’支路上作用，在1－1’支路中产生的电压u1的值。电流电压方向选关联参考方向。

（3）互易定理的第三种形式

对于一个线性电阻电路，单一电流源is在1－1’支路中作用，而在2－2’支路中产生了电流i2，i2的值等于将电流源is移到2－2’支路上作用，在1－1’支路中产生的电流i1的值。电流电压方向选关联参考方向。

（4）互易定理应用条件

并非任何一个网络都具有互易性质。一般地说，由线性时不变的二端电阻元件、电感元件、电容元件、耦合电感器和理想变压器连接而成的网络均有此性质。含有受控电源、非线性元件、时变元件、回转器的网络都不一定具有这种性质。

1.3.4例题

1.4含有理想运算放大器的电路的分析

（常用结点电压法）

1.4.1虚短

对于公共端（地），倒向输入端与非倒向输入端电压相等。

1.4.2虚断

倒向输入端与非倒向输入端电流均为零。

1.4.3虚地

运放的一个输入端接地，另一个没有接地的输入端的电压将为零。

1.4.4例题

1.5非正弦周期信号电压、电流有效值及功率求解

1.6二端口网络Y、Z参数的计算（含受控源）

1.6.1Y参数

1.6.2Z参数

1.6.3Y矩阵与Z矩阵的关系

1.7串并联谐振

含R、L、C的一端口电路，在特定条件下出现端口电压、电流同相位的现象时，称电路发生了谐振。

1.7.1串联谐振

（1）串联电路实现谐振的方式：

①LC不变，改变ω

由电路参数决定，一个RLC串联电路只有一个对应的，当外加电源频率等于谐振频率时，电路发生谐振。

②电源频率不变，改变L或C（常改变C）

（2）RLC串联电路谐振的特点

①谐振时与同相，入端阻抗为纯电阻，即Z=R，阻抗值最小。

②LC上的电压大小相等，相位相反，串联总电压为零，即，LC相当于短路。

③品质因数Q，Q是反映谐振回路中电磁振荡程度的量，Q越大，总能量就越大，维持振荡所消耗的能量愈小，振荡程度越剧烈，则振荡电路的品质愈好。

④谐振时的功率,电源向电路输送电阻消耗的功率，电阻功率达最大。

电源不向电路输送无功。电感中的无功与电容中的无功大小相等，互相补偿，彼此进行能量交换。

⑤能量关系

L、C的电场能量和磁场能量作周期震荡性的交换，而不与电源进行能量交换。

总能量不随时间变化，且等于最大值。

1.7.2并联谐振

RLC并联谐振特点

①入端导纳为纯电导，导纳值最小，端电压达最大。

②LC上的电流大小相等，相位相反，并联总电流为零，也称电流谐振。

③品质因数

④

功率

⑤能量

1.8割集、关联、回路矩阵

1.8.1割集矩阵

设一个割集由某些支路构成，则称这些支路与该割集关联。

割集方向：移去割集所有支路，G被分割成两部分后，从其中一部分指向另一部分的方向。每一个割集只有两个可能的方向。

▶独立割集矩阵（简称割集矩阵）

设有向图的结点数为n,支路数为b,则该图的独立割集数为（n-1）。

割集矩阵为一个（n-1）×b的矩阵，用Q表示。Q的行对应割集，列对应支路。割集矩阵Q的任一元素定义如下：

=+1，表示支路k与割集j关联，并且它们的方向一致；

=-1，表示支路k与割集j关联，并且它们的方向相反；

=0，表示支路k与割集j无关联。

如果选一组单树枝割集为一组独立割集，割集矩阵就称为基本割集矩阵，用表示。

1.8.2关联矩阵

设一条支路连接于某两个结点，则称该支路与这两个结点相关联。设有向图的结点数为n,支路数为b,且所有结点与支路加以编号。于是，该有向图的关联矩阵为一个（n*b）阶的矩阵，用表示。它的行对应结点，列对应支路。它的任一元素定义如下：=+1,表示支路k与结点j关联并且它的方向背离结点；

=-1，表示支路k与结点j关联并且它指向结点；

=0，表示支路k与结点j无关联。

如果把的任一行划去，剩下的（n-1）×b矩阵用A表示，称为降价关联矩阵。（被划去的行对应的结点可以当做参考结点）

1.8.3回路矩阵

一回路由某些支路组成，则这些支路与该回路关联。设有向图的独立回路数为l，支路数为b，对所有独立回路和支路加以编号，于是，设有向图的回路矩阵是一个l×b的矩阵，用B表示。B的行对应一个回路，列对应支路，它的任一元素，定义如下：

=+1，表示支路k与回路j关联，并且它们的方向一致；

=-1，表示支路k与回路j关联，并且它们的方向相反；

=0，表示支路k与回路j无关联。

如果所选独立回路组是对应于一个树的单连枝回路组，这种回路矩阵就称为基本回路矩阵，用表示。

二、计算题

2.1含有耦合电感的电路列写方程

★常见去耦合

例题：

2.2一阶电路的时域分析

（1）时间常数的求解

①将独立源置零，电压源开路，电流源短路

②从电容/电感两端看入电阻网络，求

③，   （单位为s）

（2）三要素法：

（3）解题步骤

 

2.3二瓦计法测功率

二瓦计法的理论依据是基尔霍夫电流定律，即：在集总电路中，任何时刻，对任意结点,所有流入流出结点的支路电流的代数和恒等于零。也就是说，两根火线的流入电流等于第三根火线的流出电流，或者说，三根火线的电流的矢量和等于零，即：ia+ib+ic=0　　（1）

假设三相负载的中线为N，依据电压的定义：

　　uab=uan-ubn，ucb=ucn-ubn　　（2）

　　三相瞬时功率：

　　p=uan*ia+ubn*ib+ucn*ic，　　（3）

　　将式（1）和式（2）代入式（3），得：

　　p=uan*ia+(-ubn*ia+ubn*ia)+ubn*ib+ucn*ic

　　=uab*ia+ubn(ia+ib)+ucn*ic

　　=uab*ia+ubn(-ic)+ucn*ic

　　=uab*ia+ucb*ic。

　　有功功率等于瞬时功率在一个周期内求积分再求平均，得到：P=P1+P2

　　P为三相电路有功功率的总和，P1为uab*ia在一个周期内的积分的平均值，P2为ucb*ic在一个周期内的平均值。在正弦稳态电中：P=UAB*IA*cosφAB+UCB*IC*cosφCB

　　即：P1=UAB*IA*cosφAB，P2=UCB*IC*cosφCB

　　式中，UAB、IA、UCB、IC均为正弦电压电流的有效值，φAB为UAB和IA的相位差，φCB为UCB和IC的相位差。

　　从变换的公式中可以看出，采用这种方法进行三相总功率测量时，只需要测量两个电压和两个电流，这就是二瓦计法的推导原理及由来。

　　二瓦计法测量时，三相电路总功率等于两块功率表的功率之和，每块功率表测量的功率本身无物理意义。

2.4拉普拉斯变换求解二阶电路

2.4.1拉普拉斯变换的基本性质

(1)线性性质

(2)微分性质

设则

 

(3)积分性质

设则

式中

(4)时移性质

(5)频移性质

2.4.2拉普拉斯逆变换

拉普拉斯逆变换可以表示为已知函数f（t）的拉普拉斯变换F（s），求原函数f（t）的运算为拉普拉斯反变换。其公式为：

▶常见逆变换

2.4.3电路的基本定理的复频域形式

（1）电阻元件

在复频域中，电阻电压的象函数与电阻电流的象函数之间也服从欧姆定律， 即

（2）电容元件

在复频域中，电容元件电压 -电流关系的复频域形式为 或其复频域的戴维宁模型、诺顿模型如图

（3）电感元件

在复频域中， 电感元件电压 -电流关系的复频域形式为 UL (s) sLI L (s) LiL (0 ) 或其复频域的戴维宁模型、诺顿模型如图
 

★★★解题步骤

（1）由换路前的电路计算,

（2）画出运算电路模型，注意运算阻抗的表示和附加电源的作用

（3）应用前面各章介绍的计算方法求实函数

（4）反变换求原函数