python 等深分箱法(均值平滑技术、边界值平滑技术)
文章目录
- python 等深分箱法(均值平滑技术、边界值平滑技术)
-
- 理论学习
- 实验及结果
-
- 等深分箱法(均值平滑技术、边界值平滑技术)
- 等宽分箱法(均值平滑技术、边界值平滑技术)
python 等深分箱法(均值平滑技术、边界值平滑技术)
理论学习
首先,仔细了解熟悉掌握了等深分箱法,等宽分箱法,均值平滑技术,边界值平滑技术,看了好几个博客,个人觉得讲的最清晰明了,对我帮助最大的是数据挖掘如何分箱以及如何对每个箱子中的数据进行平滑处理,这篇博客不仅对等深等宽分箱,均值,边界值平滑技术做了定义解释,而且用了几个例子让我有了更为直观的理解。
之后根据学到的知识,设想如何编写成算法实现,根据老师的提示在老师之前发的《python三剑客》电子书中查找到了一些可以用到的numpy库中的高效函数。对于要处理的数据用numpy中的array函数快速定义,关于分箱,等深分箱法很快找到了numpy中的reshape函数,同时较快的实现了等深分箱法均值平滑技术和边界值平滑技术。对于等宽分箱法,没有在numpy中找到可用函数,在上网查找资料时,查到了groupby分组函数,但是仔细阅读后发现,不适用于当前所要解决的等深分箱问题,找了很多博客,论坛什么的最后发现了pandas中的cut函数,然后对cut函数进行学习,通过python cut和qcut的用法以及区别和
pandas的分段函数cut()两篇博客,以及自己编写代码验证对cut函数有了清晰地了解。通过pandas的分段函数cut求得每个区间包含的数据量,然后据此对数据进行等宽划分,最后根据等深分箱中编写的均值平滑技术和边界值平滑技术的算法修改适应等宽分箱法
实验及结果
请分别以等深分箱法和等宽分箱法对下列数据进行平滑处理,并且分别采用均值平滑技术和边界值平滑技术,分箱个数自定,将最终数据集输出到控制台上。
原数据集为:{60,65,63,66,67,69,71,72,74,76,77,82,84,87,90},可以使用任何您熟悉的语言进行编码实现。
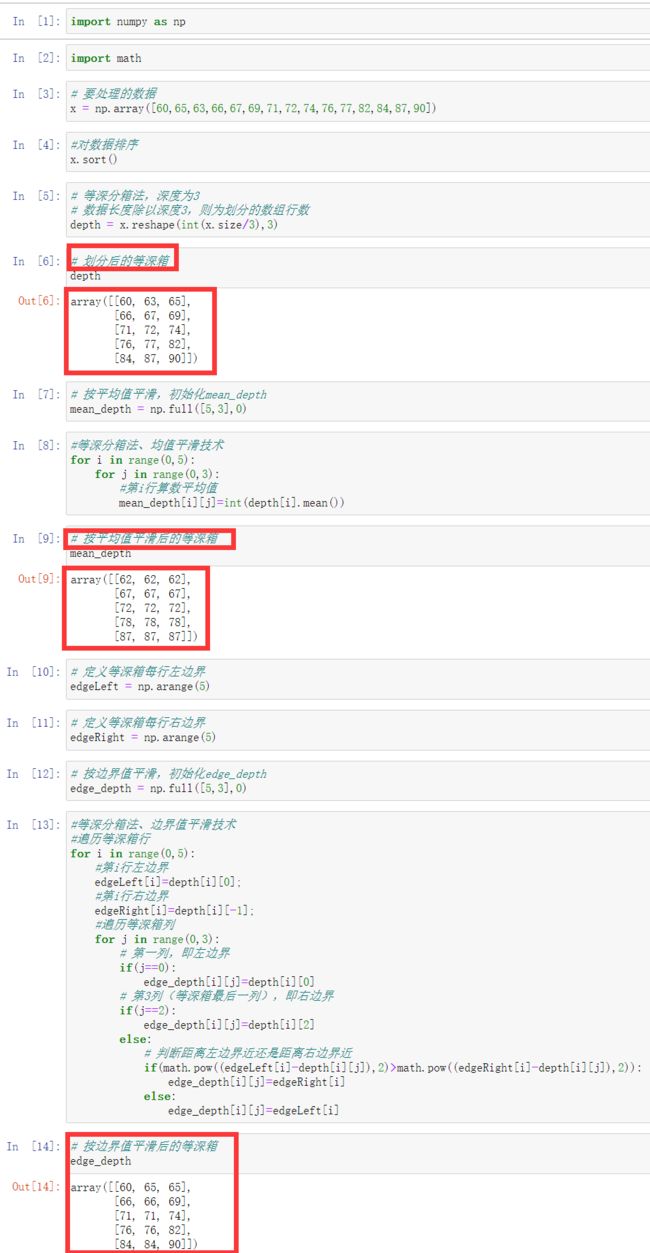
等深分箱法(均值平滑技术、边界值平滑技术)
import numpy as np
import math
# 要处理的数据
x = np.array([60,65,63,66,67,69,71,72,74,76,77,82,84,87,90])
#对数据排序
x.sort()
# 等深分箱法,深度为3
# 数据长度除以深度3,则为划分的数组行数
depth = x.reshape(int(x.size/3),3)
# 划分后的等深箱
depth
# 按平均值平滑,初始化mean_depth
mean_depth = np.full([5,3],0)
#等深分箱法、均值平滑技术
for i in range(0,5):
for j in range(0,3):
#第i行算数平均值
mean_depth[i][j]=int(depth[i].mean())
# 按平均值平滑后的等深箱
mean_depth
# 定义等深箱每行左边界
edgeLeft = np.arange(5)
# 定义等深箱每行右边界
edgeRight = np.arange(5)
# 按边界值平滑,初始化edge_depth
edge_depth = np.full([5,3],0)
#等深分箱法、边界值平滑技术
#遍历等深箱行
for i in range(0,5):
#第i行左边界
edgeLeft[i]=depth[i][0];
#第i行右边界
edgeRight[i]=depth[i][-1];
#遍历等深箱列
for j in range(0,3):
# 第一列,即左边界
if(j==0):
edge_depth[i][j]=depth[i][0]
# 第3列(等深箱最后一列),即右边界
if(j==2):
edge_depth[i][j]=depth[i][2]
else:
# 判断距离左边界近还是距离右边界近
if(math.pow((edgeLeft[i]-depth[i][j]),2)>math.pow((edgeRight[i]-depth[i][j]),2)):
edge_depth[i][j]=edgeRight[i]
else:
edge_depth[i][j]=edgeLeft[i]
# 按边界值平滑后的等深箱
edge_depth
等宽分箱法(均值平滑技术、边界值平滑技术)
import numpy as np
import pandas as pd
import math
# 要处理的数据
x = np.array([60,65,63,66,67,69,71,72,74,76,77,82,84,87,90])
#对数据排序
x.sort()
# 定义等区间
bins = [60,70,80,90,100]
# 对数据按区间分段,right=False代表区间左闭右开
x_cuts = pd.cut(x,bins,right=False)
# number数组即为每个区间的数据数量
number=pd.value_counts(x_cuts)
# 取所有区间中最大的数据数量
rows = number.max()
# 定义初始化等宽箱
widthList = np.full([4,rows],0)
size = x.size
# 将要处理的数据x按照等宽分箱法分箱
i=0
for j in range(0,4):
for a in range(0,number[j]):
widthList[j][a]=x[i]
i=i+1
# 划分后的等宽箱,非零值
widthList
# 按平均值平滑,初始化mean_width
mean_width = np.full([4,rows],0)
#等宽分箱法、均值平滑技术
for i in range(0,4):
for j in range(0,number[i]):
#第i行算数平均值
mean_width[i][j]=int(widthList[i].sum()/number[i])
# 按平均值平滑后的等宽箱
mean_width
# 定义等深箱每行左边界
edgeLeft = np.arange(4)
# 定义等深箱每行右边界
edgeRight = np.arange(4)
# 按边界值平滑,初始化edge_width
edge_width = np.full([4,rows],0)
#等宽分箱法、边界值平滑技术
#遍历等宽箱行
for i in range(0,4):
# 第i行左边界
edgeLeft[i]=widthList[i][0];
# 第i行右边界
edgeRight[i]=widthList[i][number[i]-1];
#遍历等宽箱列
for j in range(0,number[i]):
# 第一列,即左边界
if(j==0):
edge_width[i][j]=widthList[i][0]
# 等深箱最后一列,即右边界
if(j==(number[i]-1)):
edge_width[i][j]=widthList[i][number[i]-1]
else:
# 判断距离左边界近还是距离右边界近
if(math.pow((edgeLeft[i]-widthList[i][j]),2)>math.pow((edgeRight[i]-widthList[i][j]),2)):
edge_width[i][j]=edgeRight[i]
else:
edge_width[i][j]=edgeLeft[i]
#等宽分箱法、边界值平滑技术
#遍历等宽箱行
for i in range(0,4):
# 第i行左边界
edgeLeft[i]=widthList[i][0];
# 第i行右边界
edgeRight[i]=widthList[i][number[i]-1];
#遍历等宽箱列
for j in range(0,number[i]):
# 第一列,即左边界
if(j==0):
edge_width[i][j]=widthList[i][0]
# 等深箱最后一列,即右边界
if(j==(number[i]-1)):
edge_width[i][j]=widthList[i][number[i]-1]
else:
# 判断距离左边界近还是距离右边界近
if(math.pow((edgeLeft[i]-widthList[i][j]),2)>math.pow((edgeRight[i]-widthList[i][j]),2)):
edge_width[i][j]=edgeRight[i]
else:
edge_width[i][j]=edgeLeft[i]