Surface-2 PCL学习记录-7 Fast triangulation of unordered point cloud（ 使用贪婪三角化，完成无序点云的模型重建）功能及用法解析

本文大致介绍了PCL点云库中，Fast triangulation of unordered point cloud功能包的大致原理及使用方法；这个功能包背后的原理是基于德劳内分割的贪婪三角形分割法。

---

 一.PCL点云库的贪婪三角化的功能大致原理

     1.1 PCL点云库的贪婪三角化的功能和特点：

           ->主要功能是将无序点云进行分割，通过点云重建生成一个可供后续使用的连续曲面模型；

           -> 其实就是将RGBD相机采集到的点云，经过降采样，滤波，移除离群点等处理后，生成一个连续的曲面模型（将离散的点，拼成一个曲面)

           -> 贪婪三角化有较强的局限性，比较适用于连续光滑曲面的点云，并且点云密度较为统一的情况下。

            ->除了贪婪三角化以外，还有其他插值和逼近法等方法可以用来做曲面重建。

    1.2 PCL点云库进行贪婪三角化的大致过程为：

            -> 1. 首先将点云数据通过法线投影到某一个二维坐标平面内（注意：点云格式需要包含法向信息，即pcl::PointNormal).

            -> 2.  然后对投影得到的点云做平面内的三角化，从而得到各点的拓扑连接关系。平面三角化的过程中用到了基于Delaunay三角剖分的空间区域增长算法.

             -> 3. 最后根据平面内投影点的拓扑连接关系确定各原始三维点间的拓扑连接，所得三角网格即为重建得到的曲面模型。

    1.3 贪婪三角化算法的主要原理(Delaunay 三角剖分)（目前只涉及到原理，后续用到详细算法时会补充）

          ->贪婪三角化主要使用的三角抛分方法为：Delaunay 三角剖分; 这个方法广泛地备用在了数值分析和图形学等学科，是一项比较重要的预处理技术。

          -> 贪心投影三角化方法第2步就是利用Delaunay 三角剖分，它通过选取一个样本三角片作为初始曲面，不断扩张延伸曲面的边界，直到所有符合几何正确性和拓扑正确性的点都被连上，最后形成一张完整的三角网格曲面。

          ->Delaunay 三角剖分原理：

               原理： 主要的原理为，在统一平面上的点云的点，任意三角形的外接圆内部，不允许有其他的点。

                                                          

               图源：https://blog.csdn.net/qq_30815237/article/details/86313534

二.使用贪婪三角化，通过点云重建模型的代码（代码有拼写Bug，后续会更新）

#include         //定义了所有点云类型
#include           //点云文件输入输出
#include  //kdtree搜索对象的头文件
#include   //法向量相关
#include          //贪婪投影三角化法的定义
#include 

int main(int argc, char ** argv){
   //Step1: 首先创建点云对象，并读取PCD文件内容，存到点云对象内,并完成点云格式转化
   pcl::PointCloud::Ptr cloud (new pcl::PointCloud);
   pcl::PCLPointCloud2 cloud_blob;
   pcl::io::loadPCDFile ("bun0.pcd",cloud_blob);
   pcl::fromPCLPointCloud2 (cloud_blob,*cloud);


   //Setp2: 创建法向量估计对象，并查找点云的法向信息，并存入包含有法向信息的对象中
   pcl::NormalEstimation n;                               //创建法向量预估对象，输入XYZ输出Normal
   pcl::PointCloud::Ptr normals(new pcl::PointCloud);      //创建一个存储预估后法向量的对象
   pcl::search::KdTree::Ptr tree (pcl::search::KdTree);//定义KdTree指针
   tree->setInputCloud(cloud); //！！用Cloud构建tree对象
   n.setInputCloud(cloud);     //为法向估计对象设置输入点云
   n.setSearchMethod(tree);    //设置搜索方法
   n.setKSearch (20);          //设置k搜索的K值为20
   n.compute (*normals);       //将法线的查找结果存到normal对象内

   //Step3. 在第二步中，已经将包含有法向信息的点云存储到了normal对象中
   //       由于进行三角化时需要点云同时具有XYZ及法向，因此使用concatenateFields语句将原始点云+法向点云汇总到cloud_with_normals中
   pcl::PointCloud::Ptr cloud_with_normals(new pcl::PointCloud);
   pcl::concatenateFields (*cloud, *normals, *cloud_with_normals);                   //注意这句是将三个点云统一在一起了

   //Step4：创建用于三角化的KDTREE对象,并将待处理的点云输入进去
   pcl::search::KdTree::Ptr tree2 (pcl::search::KdTree);
   tree2->setInputCloud(cloud_with_normals); //！！利用点云构建tree对象 

   //Step5: 创建贪婪三角化对象
   pcl::GreedyProjectionTriangulation gp3;
   pcl::PolygonMesh triangles;          //！！存储最终的三角化网格模型

   //Step6 :设置三角化参数，重要！！
  gp3.setSearchRadius (0.025);           //1.设置三角化时，两个点之间的最大距离（也就是三角形边长）
  gp3.setMu (2.5);                       //2. 设置每个样本点搜索邻域的大小，此处为2.5个体素栅格
  gp3.setMaximumNearestNeighbors (100);  //3. 设置没一个样本点可搜索邻域个数为100
  gp3.setMaximumSurfaceAngle(M_PI/4);    //4. 设置某点法线方向偏离样本点的最大角度为45度（超出舍弃）
  gp3.setMinimumAngle(M_PI/18);          //5. 设置三角化后，内角的最小角度为10度
  gp3.setMaximumAngle(2*M_PI/3);         //6. 设置三角化后，内角的最大角度为120度
  gp3.setNormalConsistency(false);       //设置保证法线朝向一致与否

  // Step7 :Get result
  gp3.setInputCloud (cloud_with_normals); //将点云输入设置好的三角化对象中
  gp3.setSearchMethod (tree2);            //搜索方式为tree2
  gp3.reconstruct (triangles);            //！！将三角化后的网格模型存储到对象中


  std::vector parts = gp3.getPartIDs();
  std::vector states = gp3.getPointStates();

  pcl::io::saveVTKFile("mesh.vtk", triangles);

  // Finish
  return (0);
}

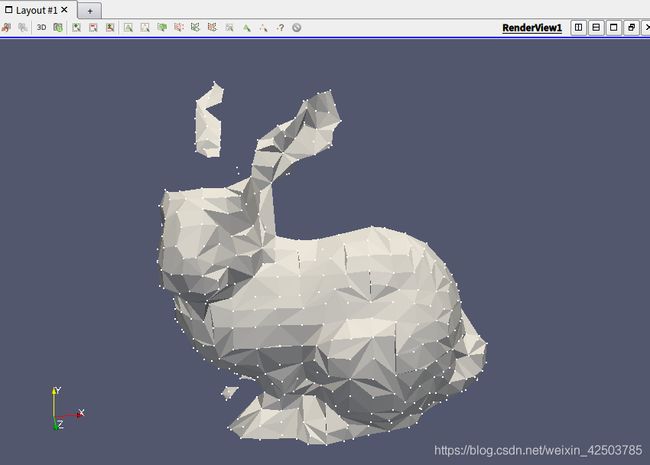
重构的模型格式为.vtk， 可以用paraview打开。