从头开始复习算法之让你彻彻底底的搞清楚BFS和DFS

最近又有点学不进去了，不知道是不是天气热的缘故哈，没办法只好写一点算法来保持学习的路线不间断咯。 关于BFS和DFS，这是我们在面试的时候经常会遇到的两个基础算法，为什么说基础呢？因为它理解了之后才10行左右的代码，你说基础不基础？

一、 BFS

BFS，全称：Breadth First Search。中文翻译为广度优先搜索或者是宽度优先搜索，具体是怎么回事儿呢？
首先来用下面一颗的树来引入一下广度优先搜索的实现步骤：

如上图所示，我们先用一棵树来引入广度优先搜索。为什么要用树呢？因为我觉得树来入门是最简单的，也是最容易理解的。
首先按照广度优先搜索的方法，我们就应该就是这样来搜索：
A->B->C->D->E->F
或者是：
A->C->B->F->D->E

我先来从结果分析上面的遍历结果，我发现广度优先搜索有这样的特点对：

• 先从根节点处查找，然后一层一层的往下查找。
  怎么理解呢？首先查找A也就是第一层，然后再查找BC，也就是第二层，最后查找DEF 也就是第三层。
• 查找子层的时候，应该按照父层的顺序来查找子层。
  怎么理解呢？首先查找A节点，然后查找A的子层B和C，当然我们在查找A子层的时候先来查找的B节点，那么在查找B的子节点的时候就要优先查找B的子节点。同理如果第二层里面先查找C也是一样。
• 广度优先搜索的搜索结果并不唯一。

通过上面的结果来分析，其实我们很容易发现广度优先算法有点队列的意味在里面。
怎么理解呢？来看下面一套图：

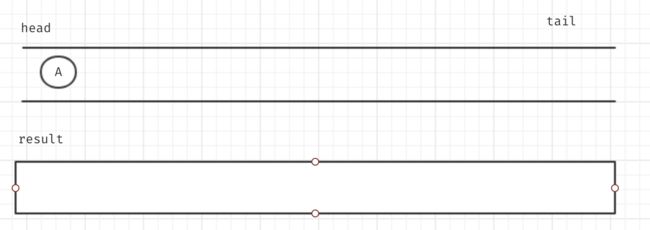
首先新建一个队列，先去查找一下树的根结点，并且将根结点A放入队列中。

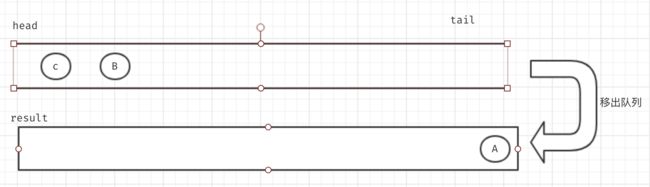
移出节点A，并且把A的子节点加入到队列中。

移出节点B，并且把B的子节点加入到队列中。

...
依次类推，就将所谓的最后的广度优先搜索的路线给画出来了：

最终结果

通过前面的探究，我们大概晓得了广度优先搜索的一个大致流程，也差不多知道其实现的规则有点类似于队列。此时可能有人会说了，你只是讲解了一个简单的树，而我们看到的BFS一般是用图来展示的。
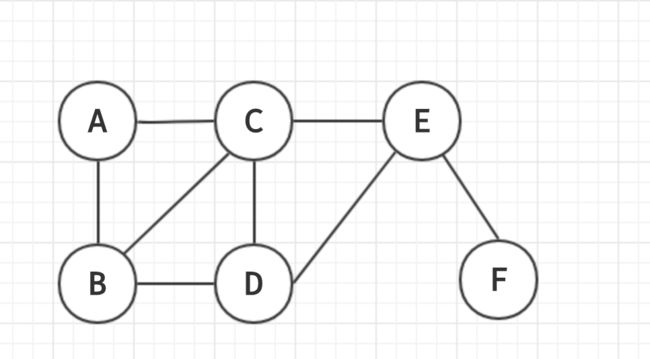
针对上面的疑问，我们首先来画一个无向图。

其实在我的理解里面：图和树最大的区别就是树有专门的起点，但是图却没有固定的起点。我们可以从任何一个点做起点来去搜索，例如：从A点出发，搜索结果是：
A->B->C->D->E->F
从E点出发：
E-> C->D->F->A->B
...

这样，我们其实就可以把之前树的那一套类似到图中，只不过图没有起点罢了，并且将树的子层换成了与指定节点相连的节点。这样类比之下也可以用队列来实现。具体的代码如下：

首先我们建立一张图：

let graph = {
    'A':['B','C'],
    'B':['A','C','D'],
    'C':['A','B' ,'D','E'],
    'D':['B','C','E'],
    'E':['C','D','F'],
    'F':['E']
}

然后BFS的实现代码如下：

function bfs(graph,startPoint){
    let queue = [];
    let result = []

    queue.push(startPoint);
    result.push(startPoint);

    while(queue.length>0){
        let point = queue.shift();
        let nodes = graph[point];
        for(let node of nodes){
            if(result.includes(node)) continue;
            result.push(node);
            stack.push(node);
        }
    }
    return result

}

二、DFS

好了，前面谈到了广度优先搜索，那么什么是深度优先搜索呢？
首先我来用一套图集来辅助理解深度优先搜索的历程：

首先选定起点为A（起点是任意的），然后从A出发，搜索到B

然后再从B出发，搜索到C

再从C出发搜索到E

再从E出发搜索到D，此时整张图都没有与D相连但是没被搜索到的节点了，此时该怎么办呢？

如果搜索到没有可以搜索的节点，就应该回溯到最近存在相邻可以的节点处继续搜索。

总之，我对于深度优先搜索的理解就是：

• 访问顶点A
• 依次从A的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和A有路径相通的顶点都被访问；
• 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

这样看来，深度优先是不是有一点栈的意思在里面呢？怎么理解哦，我们再来看下面一套图。

首先我们从A出发，将节点A移入栈，然后将A移出栈

将A的子节点C，B移入栈内。

然后将B移出栈，并将与B相连的D，C节点移入栈内

然后将C移出栈，将与C相连的D，E节点移入栈内

然后将E移出栈，将与E相连的F，D节点移入栈内

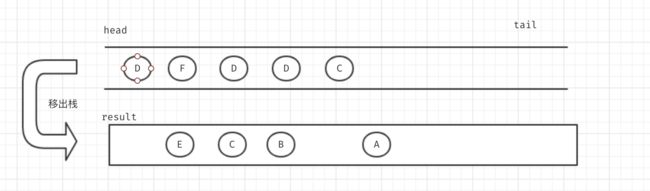
然后将D移除栈，我们发现并没有可用的新节点了，就不再移入直接移出。

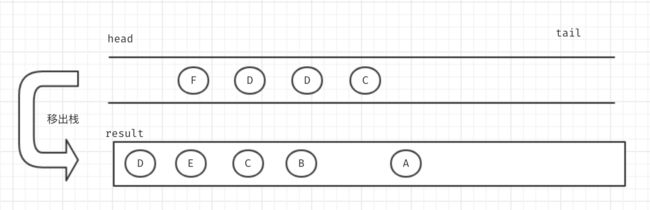
移出F节点

当我在移除新D节点的时候，发现D节点已经被移出过了。此时我们就将该节点丢弃，同样后面的节点也是一样。最后就完成了深度优先搜索。

通过上面的图级演示是不是很容易就能看出来深度优先搜索的实现原理呢？下面我们用代码的方式来去演示一下其原理吧：

function dfs(graph,startPoint){
    let stack = [];
    let result = []

    stack.push(startPoint);
    result.push(startPoint);

    while(stack.length>0){
        let point = stack.pop();
        let nodes = graph[point];
        for(let node of nodes){
            if(result.includes(node)) continue;
            result.push(node);
            stack.push(node);
        }
        

    }
    return result

}

说在最后

说了这么多，感觉午休的时间都所剩无几了，感觉自己还是没有把这部分的内容讲清楚。本来想额外写一点关于广度优先搜索的更深层次的用法的（作为很多图形结构的基础，其实应用还是比较广的），但我还是需要睡的呀！反正中午看来是说不完了。关于还没写完的内容呢，我这里提及一下：
如果相邻节点之间的距离相同的情况下，我们想求广度优先搜索的最短路径怎么来求呢？
如果相邻节点之间的距离不同呢？我们应该如何来计算呢
如果明天中午有机会的话，我会细细讲解这一块的内容的，敬请期待哦！