论文笔记009-《A Vectorized Relational Graph Convolutional Network for Multi-Relational Network Alignment》
1. 简介
《A Vectorized Relational Graph Convolutional Network for Multi-Relational Network Alignment》
来源:IJCAI-2019
链接:论文链接
代码:[暂无]
关键字:Graph Convolutional Network、Embedding-based、Entity Alignment
2. Abstract
目前多关系网络(例如知识图谱)对齐工作对上层的AI应用有很重要的意义。现有的基于图卷积网络(Graph Convolutional Network,GCN)的对齐模型并没有充分地利用多关系的信息,也就是关系的类别信息。因此作者提出一种关系向量化的图卷积网络VR-GCN,来同时学习实体的表示和关系的表示,并基于此网络构建了对齐框架AVR-GCN用于多关系网络对齐任务。
3. Introduction
近年来网络对齐在工业界和学术界均受到很大的关注,其旨在不同的网络中找到具有相同语义的等价节点或等价关系。以知识图谱为例,对齐不同语言的知识图谱,有利于构建更完备的知识网络,其对提升知识推理、跨领域推荐等任务的准确率和鲁棒性效果显著。
基于表示学习的模型由于其高效性也被用到网络对齐任务中。根据其是否对网络内关系进行表示,可以分为单关系网络(Single-relational networks)表示方法,DeepWalk和Node2Vec,其中里面的关系都是一种类型,从而只对节点进行嵌入学习;多关系网络(Multi-relational networks)表示方法,如:TransE及其拓展的工作,其中不仅要对结点进行嵌入学习,其关系有很多种类,也会进行嵌入学习。
随着深度学习的发展,以图卷积网络GCN为代表的方法对图表示相关任务有很好的效果。然而,传统的基于频谱的GCN只能处理无向单关系网络,因为其要求归一化图拉普拉斯算子为实对称正半定矩阵,以便于进行图的傅立叶变换,这也表明邻接矩阵必须是对称的,并且二维的邻接矩阵也将边限制为相同类型,即单一关系。为了在图卷积中增加对多关系的支持,R-GCN对每一关系学习一个映射矩阵,用于改变实体在累计邻居权重时考虑来自不同关系的影响,但R-GCN也没有显式地对关系进行表示。
因此,本文作者提出同时对实体和关系进行表示的图卷积网络VR-GCN,其具备以下几个特点:
- 不仅对结点进行embedding学习,还有显式的关系embedding学习。
- 实体角色区分:实体作为头实体或尾实体时采取不同的卷积操作,同时也体现图的有向性。
- 翻译模型的性质:学习到的表示具备形如TransE的 h + r ≈ t h + r \approx t h+r≈t的性质。
基于VR-GCN,作者在实体和关系层面上设计了对齐的优化目标函数,得到网络对齐模型AVR-GCN,其在实体对齐,关系对齐以及链接预测各方面上均表现不错。
3. Relation Work
本文的研究主要分为Network Embedding和Knowledge Graph Alignment这两部分。
3.1. Network Embedding
网格嵌入就是对网络的结点或者边进行嵌入学习,对于单关系网络,DeepWalk和Node2vec扩展了skip-gram的原理去学习网路结构,而LINE则是通过一阶邻接点或二阶邻接点来产生结点的表示,后续的Trans系列的模型都是以 h + r ≈ t h + r \approx t h+r≈t来表示结构的。由于神经网络优越的提取特征特性,人们将CNN网络尝试运用在非欧拉空间的图结构上,形成GCN网络,其在半监督的分类问题上表现非常优秀。后续再其基础上,有人提出了GAT的注意力机制的网络,其结点通过邻接点的重要性进行表示学习,最后就是一个R-GCN网络中结点通过对关系的类型进行感知,并结合其关系的权重进行结点嵌入学习。总的来说,都没有对关系进行嵌入学习,结合其以后效果来看,对关系的嵌入学习可能对实体对齐有很大的提升。
3.2. Knowledge Graph Alignment
网络的对齐工作通过结构信息以及原先对齐的种子实体对。MTransE方法将网络分别进行嵌入学习,然后学习一个变化到同一空间的参数矩阵进行实体对齐匹配,相反ITransE则就是在统一空间中进行嵌入学习,然后不断的迭代进行实体对齐。AlignE则是采用Trans进行嵌入学习,同时共享参数将网络编码在同一空间,NTAM则就是学习了一个概率分布的模型,后续的**GCN(SE)**使用传统的GCN将不同空间的实体嵌入到同一的空间中去,其将这种关系视为对实体具有影响力的,与不同实体的连接数量成比例的权重类型关系。上述的方法均没有考虑对关系进行嵌入表达,而且考虑到前面的研究中关系对效果的提升,作者自然而然就想到了将关系提升到和结点同一个层度,进而提出了其自己的方法VR-GCN。
4. Model
知识图 K G = ( E , R , T ) K G=(E, R, T) KG=(E,R,T)为有向网络,其中 E , R E, R E,R 和 T T T 表示实体、关系和三元组。一个三个一组 ( h , r , t ) (h, r, t) (h,r,t)表示一个尾实体 t t t 通过关系 r r r 与头实体 h h h 连接,知识图谱对齐是去在 K G i = ( E i , R i , T i ) K G_{i}=\left(E_{i}, R_{i}, T_{i}\right) KGi=(Ei,Ri,Ti)和 K G j = ( E j , R j , T j ) K G_{j}=\left(E_{j}, R_{j}, T_{j}\right) KGj=(Ej,Rj,Tj)之间查找已对齐的实体和关系。对于预先对齐的实体/关系的先验知识锚。它们被表示为锚实体对的集合 E a = { ( e i , e j ) ∣ e i ∈ E i , e j ∈ E j } E_{a}=\left\{\left(e_{i}, e_{j}\right) \mid e_{i} \in E_{i}, e_{j} \in E_{j}\right\} Ea={ (ei,ej)∣ei∈Ei,ej∈Ej} 和锚点关系集对 R a = { ( r i , r j ) ∣ r i ∈ R i , r j ∈ R j } R_{a}=\left\{\left(r_{i}, r_{j}\right) \mid r_{i} \in R_{i}, r_{j} \in R_{j}\right\} Ra={ (ri,rj)∣ri∈Ri,rj∈Rj}。
4.1. VR-GCN Framework
和以往的GCN模型进行比较,其VR-GCN不仅可以对结点进行嵌入学习,而且对关系也能很好的进行嵌入学习。其整合了GCN和翻译模型优点,其更新传播规则如下,VR-GCN模型结构如下:
h i l + 1 = σ ( ( ∑ r ∈ N r ∑ t ∈ N t r c ( h t l , h r l ) + ∑ r ∈ N r ∑ h ∈ N h r c ^ ( h h l , h r l ) + h i l ) W l ) (1) h_{i}^{l+1}=\sigma\left(\left(\sum_{r \in N_{r}} \sum_{t \in N_{t}^{r}} c\left(h_{t}^{l}, h_{r}^{l}\right)+\sum_{r \in N_{r}} \sum_{h \in N_{h}^{r}} \hat{c}\left(h_{h}^{l}, h_{r}^{l}\right)+h_{i}^{l}\right) W^{l}\right) \tag {1} hil+1=σ⎝⎛⎝⎛r∈Nr∑t∈Ntr∑c(htl,hrl)+r∈Nr∑h∈Nhr∑c^(hhl,hrl)+hil⎠⎞Wl⎠⎞(1)

其中 N r N_{r} Nr 表示和实体 i i i 有关的关系 r r r 的集合,而 N t r / N h r N_{t}^{r} /N_{h}^{r} Ntr/Nhr 分别表示和实 i i i 通过关系 r r r 联系起来的尾结点/头结点的集合, h h l / h r l / h t l ∈ R d ( l ) h_{h}^{l}/h_{r}^{l}/h_{t}^{l} \in R^{d(l)} hhl/hrl/htl∈Rd(l) 分别表示第 l l l 层的头结点/关系/尾结点的表示,其 R d ( l ) R^{d(l)} Rd(l) 表示第 l l l 层的纬度,激活函数为 σ \sigma σ ,而 W l W^{l} Wl 是第 l l l 层的权重矩阵,对于 c c c 通过Trans原理演变而来,具体含义如下:
c ( h t l , h r l ) = ( h t l − h r l ) (2a) c\left(h_{t}^{l}, h_{r}^{l}\right)=\left(h_{t}^{l}-h_{r}^{l}\right) \tag {2a} c(htl,hrl)=(htl−hrl)(2a)
c ^ ( h h l , h r l ) = ( h h l + h r l ) (2b) \hat{c}\left(h_{h}^{l}, h_{r}^{l}\right)=\left(h_{h}^{l}+h_{r}^{l}\right) \tag {2b} c^(hhl,hrl)=(hhl+hrl)(2b)
那么其公式1就可以化简为如下表示形式,其中的 d i d_{i} di是归一化参数,即实体 i i i 的出入度之和:
h i l + 1 = σ ( ( 1 d i ( ∑ r ∈ N r ∑ t ∈ N t r ( h t l − h r l ) + ∑ r ∈ N r ∑ h ∈ N h r ( h h l + h r l ) ) + h i l ) W l ) (3) h_{i}^{l+1}=\sigma\left(\left(\frac{1}{d_{i}}\left(\sum_{r \in N_{r}} \sum_{t \in N_{t}^{r}}\left(h_{t}^{l}-h_{r}^{l}\right)+\sum_{r \in N_{r}} \sum_{h \in N_{h}^{r}}\left(h_{h}^{l}+h_{r}^{l}\right)\right)+h_{i}^{l}\right) W^{l}\right) \tag {3} hil+1=σ⎝⎛⎝⎛di1⎝⎛r∈Nr∑t∈Ntr∑(htl−hrl)+r∈Nr∑h∈Nhr∑(hhl+hrl)⎠⎞+hil⎠⎞Wl⎠⎞(3)
4.2. VR-GCN-based Knowledge Graph Alignment
在VR-GCN的基础上,使用共享参数的设定分别训练两个输入的网络,同时增加网络对齐的目标,可以得到知识图谱对齐框架AVR-GCN。如下图所示:
上图中不同的KG通过VR-GCN网络分别进行学习嵌入表达,然后通过共享的参数将其嵌入到同一空间中,从而简化后续的实体对齐工作。对于预先对齐的实体对种子,本文进行两部分处理工作:
1)一部分对齐的种子对作为目标函数优化的对象,对齐的实体对距离应该相距小一些,而未对齐的实体对的距离应该大一些,同时对于关系也同时考虑进去,目标函数如下:
O = ∑ ( e x , e y ) ∈ E a ∑ ( e x ′ , e y ′ ) ∉ E a [ d ( e x , e y ) + ξ − d ( e x ′ , e y ′ ) ] + α ∑ ( r x , r y ) ∈ R a ( r x ′ , r y ′ ) ∉ R a [ d ( r x , r y ) + ξ − d ( r x ′ , r y ′ ) ] (4) \begin{array}{c} O=\sum_{\left(e_{x}, e_{y}\right) \in E_{a}} \sum_{\left(e_{x}^{\prime}, e_{y}^{\prime}\right) \notin E_{a}}\left[d\left(e_{x}, e_{y}\right)+\xi-d\left(e_{x}^{\prime}, e_{y}^{\prime}\right)\right]+ \\ \alpha \sum_{\left(r_{x}, r_{y}\right) \in R_{a}\left(r_{x}^{\prime}, r_{y}^{\prime}\right) \notin R_{a}}\left[d\left(r_{x}, r_{y}\right)+\xi-d\left(r_{x}^{\prime}, r_{y}^{\prime}\right)\right] \end{array} \tag {4} O=∑(ex,ey)∈Ea∑(ex′,ey′)∈/Ea[d(ex,ey)+ξ−d(ex′,ey′)]+α∑(rx,ry)∈Ra(rx′,ry′)∈/Ra[d(rx,ry)+ξ−d(rx′,ry′)](4)
其中 ( e x , e y ) (e_x,e_y) (ex,ey)和 ( r x , r y ) (r_x,r_y) (rx,ry)是对齐的,而对于 ( e x ′ , e y ′ ) (e_x^{\prime},e_y^{\prime}) (ex′,ey′)和 ( r x ′ , r y ′ ) (r_x^{\prime},r_y^{\prime}) (rx′,ry′)是相关的未对其的实体对或者关系对, d ( x , y ) = ∣ ∣ x − y ∣ ∣ 1 d(x,y)=||x-y||_1 d(x,y)=∣∣x−y∣∣1表示两者之间的距离, ξ \xi ξ 和 α \alpha α 均是超参数。
2)一部分用来补充一些实体对,丰富两个网络之间的联系,这一部分在嵌入学习之前就会增加进去:
T a = { ( e y , r , t ) ∣ ( e x , r , t ) ∈ T x } ∪ { ( h , r , e y ) ∣ ( h , r , e x ) ∈ T x } ∪ { ( e x , r , t ) ∣ ( e y , r , t ) ∈ T y } ∪ { ( h , r , e x ) ∣ ( h , r , e y ) ∈ T y } (5) \begin{aligned} T_{a}=&\left\{\left(e_{y}, r, t\right) \mid\left(e_{x}, r, t\right) \in T_{x}\right\} \cup\left\{\left(h, r, e_{y}\right) \mid\left(h, r, e_{x}\right) \in T_{x}\right\} \\ & \cup\left\{\left(e_{x}, r, t\right) \mid\left(e_{y}, r, t\right) \in T_{y}\right\} \cup\left\{\left(h, r, e_{x}\right) \mid\left(h, r, e_{y}\right) \in T_{y}\right\} \end{aligned} \tag {5} Ta={ (ey,r,t)∣(ex,r,t)∈Tx}∪{ (h,r,ey)∣(h,r,ex)∈Tx}∪{ (ex,r,t)∣(ey,r,t)∈Ty}∪{ (h,r,ex)∣(h,r,ey)∈Ty}(5)
5. Experiment
本文首先评估了AVR-GCN框架跨语言、多关系网络中实体对齐与关系对齐任务的有效性。此外,对VR-GCN模型进行了链路预测实验,研究了该算法在多关系网络嵌入中链接预测的有效性。
5.1. Knowledge Graph Alignment
实验包括跨语言实体对齐和跨语言关系对齐,在种语言类型之间进行对齐评估,来自DBpedia所包含的真实知识图谱如:ZH - EN,JA−EN,FR−EN,具体信息如下:
评价指标:使用的是MRR和Hits@k。两个指标越大,表明模型效果越好。
Baseline:使用了:将两个向量空间进行线性变换,从而达到对齐目的的MTransE;迭代式增加训练数据的ITransE;概率模型NTAM;使用受限的Margin ranking loss的BootEA的非迭代模型AlignE;基于图卷积网络的实体对齐模型GCN-Align;以及AVR-GCN去除关系对齐目标的消融模型AVR-GCN(rl.exl.),其实验的结果如下所示:
- 实体对齐的实验对比结果
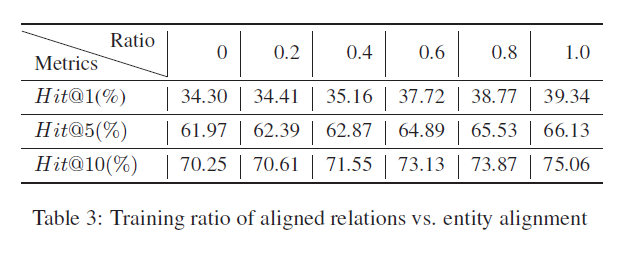
- 预先对齐的关系比例对照实验结果
- 关系对齐的实验结果
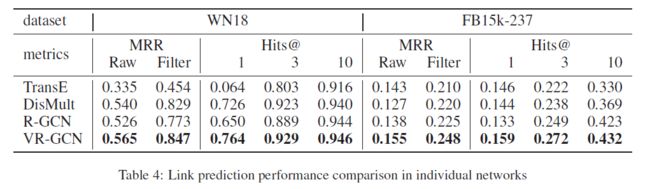
- 实体链接的实验结果
数据集:方面,使用的是链接预测任务广泛使用的公开数据集WN18和FB15k-237。
评价指标:使用的是MRR和Hits@k。两个指标越大,表明模型效果越好。
Baseline:使用了TransE,DisMult,和R-GCN。
5.2. Summary
总的来说,本文提出了一种向量化卷积关系图,网络(VR-GCN)的嵌入学习同时用于多关系的图实体和关系网络,其具有区分实体位置信息与翻译模型卷积算法采用知识图的性质的模型。然后是AVR-GCN,对齐框架基于VR-GCN,参数共享机制用于将图的嵌入连接到统一空间中对齐。锚(即预先对齐的实体和关系)是用来监督目标的函数,其目的是最小化锚点之间的距离。此外,锚还用于生成跨网络建立知识图之间的桥梁在三元组,丰富网结构之间联系。在真实数据集上的实验结果显示所提出的解决方案优于当前的实体对齐,关系对齐的以及实体链接的技术。对于未来的工作,作者计划整合注意力机制和语义信息进入模型。