19-图的最短路径

图的最短路径

迪杰斯特拉算法
贝尔曼-福特算法
弗洛伊德算法
SPFA算法(中国西南交通大学段凡丁发明)

最短路径问题分为两类，一大类是求一个顶点到其余各顶点的最短路径问题，另一大类是求各个顶点间最短路径问题。

迪杰斯特拉

迪杰斯特拉算法就是求解一个点到其余各点的最短路径算法，无向图带权图和有向带权图都适用。缺点是不适用权值为负数的图(后面会讲解原因)

算法步骤

初始的点为起点，我们用s集合存储已经确定最短路径的点的集合，那么s={v},起点加入。其余各个点到v点的权值存储在dis数组里，不是直接连接的点距离都是无穷大
从dis数组选出一个顶点u，这个点u到v点距离最小，把u加入s集合表示u已经确定了最短路径
以点u为中介点，将除了s集合存储的点以外的其余点逐个判断，如果某个点x存在dis[u]+u点到x点距离
重复2，3步骤，直到s集合包含了所有点。

我们还是直接上图看完整流程

tree24.jpg

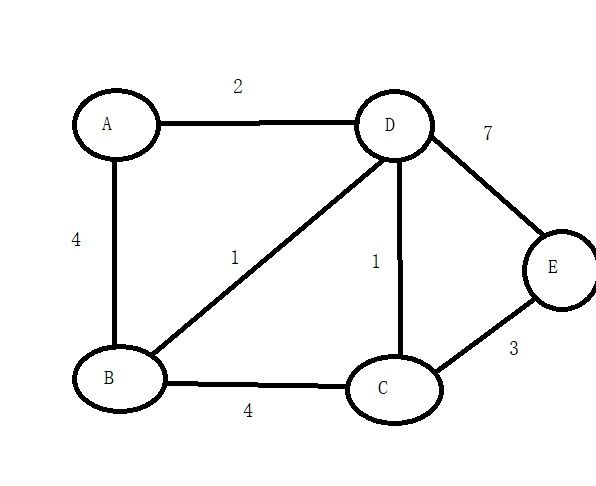
首先我们先准备几个辅助数组,我们假设从点A为起点，找其它点到点A的最短路径

节点	A	B	C	D	E
下标	0	1	2	3	4
权重	0	4	∞	2	∞
标记	1	0	0	0	0
前驱	-1	0	-1	0	-1

我来说明下，这几个数组的作用
权重数组存储每个点到A点的最短距离

前驱数组存储的是每个点前驱点下标，例如B点前驱是0，表示B和A连接,前驱是A

标记数组存储的是当前点是否已经找到了最短路径。

接下来我们准备工作做好了，开始干活了!

1.按照算法步骤，找出没被标记点中权重最小的点，我们找到了D点，将D点标记为1，表示D点以确认最短路径，然后以D点为中介判断未标记点，首先来到了B点，权重数组中B对应的是4，根据算法步骤3，我们计算出权重数组D+BD距离2+1=3 < 4(4就是权重数组B的值)所以B当前有一条路径比之前近，所以修改了B点对应的权重为3，同时更新它的前驱是D的下标。意思就是经过D点到B，更加近。同理继续看下一个未被标记的点C，继续计算权重数组D+CD距离 2+1=3 <∞,拿C点也要修改权重为3，同时更新C点前驱是D，继续看下一个未被标记点E，发现权重数组D+DE=9<∞,所以也修改E点权重为9，同步更新它的前驱是D。如下表就是第一次更新后的结果

节点	A	B	C	D	E
下标	0	1	2	3	4
权重	0	3	3	2	9
标记	1	0	0	1	0
前驱	-1	3	3	0	3

2.找出当前表中未标记点权重最小的，来到了B点和C点，我们选择B(随便哪一个都行)将B标记为1，接着逐个判断未被标记点，首先是C，权重数组B+BC距离 3+4 >3所以不修改。又来到了E，权重数组B+BE 3+∞ >9 ,也不修改，如下表就是第二次更新的结果

节点	A	B	C	D	E
下标	0	1	2	3	4
权重	0	3	3	2	9
标记	1	1	0	1	0
前驱	-1	3	3	0	3

3.找出当前表中未被标价点权重最小的是C点，将C点标记为1，然后判断未被标记的，只剩E点，权重数组C+CE距离 3+3<9 所以修改E点权重是6，更行E点前驱是C的下标，如下表就是第三次更新的结果

节点	A	B	C	D	E
下标	0	1	2	3	4
权重	0	3	3	2	6
标记	1	1	1	1	0
前驱	-1	3	3	0	2

4.找出最小，只剩下E点，直接标记E点是1，结束。

节点	A	B	C	D	E
下标	0	1	2	3	4
权重	0	3	3	2	6
标记	1	1	1	1	1
前驱	-1	3	3	0	2

有了上面一张表，我们就可以求出每个点到A点的最短路径了，我举两个点例子。

首先是点B，根据前驱下标进行寻找，B前驱下标是3，对应点D，所以B点前驱是D，接着D点前驱下标是0，对应点A，接着A点前驱下标是-1，退出。所以整个逆序路径就是B-D-A

接着看E点，前驱下标是2就是C点，C点前驱是3是D点，D点前驱下标是0，是A点，A点前驱是-1，退出,整个逆序路径是E-C-D-A

//迪杰斯特拉算法
void Dijkstra(struct MGraph *g, char obj)
{
    int *temp, *dis, *pre,index,min,k;
    temp = (int*)malloc(sizeof(int) * g->numVretexes);
    dis = (int*)malloc(sizeof(int) * g->numVretexes);
    pre = (int*)malloc(sizeof(int) * g->numVretexes);
    //找出源节点的位置
    for (int i = 0; i < g->numVretexes; i++)
    {
        if (g->vetex[i] == obj)
        {
            index = i;
            break;
        }
    }
    //初始化辅助数组
    for (int i = 0; i < g->numVretexes; i++)
    {
        temp[i] = 0;
        pre[i] = -1;
        dis[i] = g->data[index][i];
    }
    temp[index] = 1;
    for (int i = 1; i < g->numVretexes; i++)
    {
        min = MAX;
        //找出当前dis存储最小的下标
        for (int j = 0; j < g->numVretexes; j++)
        {
            if (temp[j] == 0 && g->data[index][j] < min)
            {
                min = g->data[index][j];
                k = j;//标记最小值的位置
            }
        }
        temp[k] = 1;
        index = k;
        //从该点开始，逐个判断并修改dis数组
        for (int j = 0; j < g->numVretexes; j++)
        {
            if (temp[j] == 0 && (g->data[k][j] + dis[k]) < dis[j])
            {
                dis[j] = g->data[k][j] + dis[k];
                pre[j] = k;
            }
        }
    }

    //dis数组就是源点到各个点的最短路径
    for (int i = 0; i < g->numVretexes;i++)
    {
        printf("%c-->%c(%d)\n", obj, g->vetex[i], dis[i]);
    }
    printf("\n");
}

贝尔曼-福特

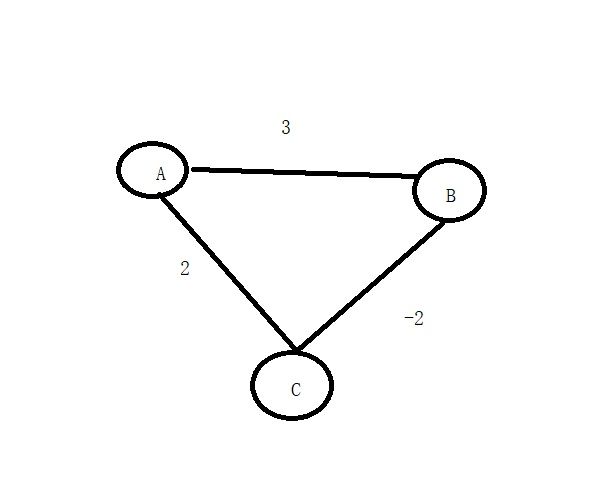
首先我们在这里回答下，为什么迪杰斯特拉算法不可以计算带负权的图。我们直接举例子分析吧

tree25.jpg

看这个图，存在带负权的边，现在我们按照迪杰斯特拉算法去求解A点到其它点的最短路径问题。

节点信息	A	B	C
下标	0	1	2
权重	0	3	2
前驱	-1	0	0
标记	1	0	0

首先选出权重最小的是点C，标记点C是1，然后判断未被标记点D 权重数组C+CB距离<权重数组B,所以修改点B对应的权重是0，且更行它的前驱是2.接着只剩下点B，标记它，完成。最终的表如下

节点信息	A	B	C
下标	0	1	2
权重	0	0	2
前驱	-1	2	0
标记	1	1	1

根据表发现，A点到C点的最短距离是2，可是我们一眼可以发现，从A到B再到C的距离是1，所以迪杰斯特拉不成立啊。什么原因？仔细看迪杰斯特拉算法的特性。它每次都找出当前权重数组最小的，找到后，就确认了这个点已经是最近的。可是如果后面其他边可能会存在负数边，会让这个点距离目标点更近。讲的有点绕，大家还是看图分析吧。

贝尔曼-福特求解思路

为了能够求解带又负值的单原最短路径问题，贝尔曼-福特从原点逐次绕过其它点，通过松弛操作以达到缩短终点的最短路径方法。

什么是松弛操作？我举个例子，假设权重数组A存储的是3,权重数组B存储的是10，而点A到B有一条边距离是2，那么你说是不是应该修改权重数组B存储的值了，先到达A点，再到达点B的距离仅仅是3+2=5,表示路过B到达A，比直接到A的路径短，修改A的权重是5。

我们准备两个数组，一个是path数组，就是前驱数组，存储路径的，另一个就是dis数组，存储权重.将它们初始化，path数组全部初始化为-1，dis数组全部初始为无穷大，并初始化原点的dis为0
因为有n个点,所以最多有n-1条边,所以需要执行n-1次循环，每次循环都对每条边进行松弛的判断。

总结下,就是对于图的每条边,将每个点进行边的松弛判断,条件成立,修改dis数组

void Bellman_Ford(struct MGraph *g, char obj)
{
    int *dis, *pre,index,temp;
    dis = (int*)malloc(sizeof(int) *g->numVretexes);
    pre = (int*)malloc(sizeof(int) * g->numVretexes);
    //找出目标点位置
    for (int i = 0; i < g->numVretexes; i++)
    {
        if (g->vetex[i] == obj) {
            index = i;
            break;
        }
    }
    //初始化dis数组
    for (int i = 0; i < g->numVretexes; i++)
    {
        dis[i] = MAX;
        pre[i] = -1;
    }
    dis[index] = 0;
    for (int k = 1; k < g->numVretexes; k++)
    {
        for (int i = 0; i < g->numVretexes; i++)
        {
            for (int j = 0; j < g->numVretexes; j++)
            {
                if (j != index && i != j && g->data[i][j] != MAX)
                {
                    if (dis[i] + g->data[i][j] < dis[j])
                    {
                        dis[j] = dis[i] + g->data[i][j];
                        pre[j] = i;
                    }
                }
            }
        }
    }
    //经过松弛后，如果还可以松弛，表示图中存在负数权回路
    temp = 0;
    for (int i = 0; i < g->numVretexes; i++)
    {
        for (int j = 0; j < g->numVretexes; j++)
        {
            if (j != index && i != j && g->data[i][j] != MAX)
            {
                if (dis[i] + g->data[i][j] < dis[j])
                {
                    temp = 1;
                    printf_s("图中存在负权回路\n");
                    return;
                }
            }
        }
    
    }
    //输出dis数组
    for (int i = 0; i < g->numVretexes; i++)
    {
        printf_s("%d ", dis[i]);
    }
    
}

SPFA算法

SPFA算法是中国老师段丁凡老师发明的，用于求单源最短路径问题的负权值问题。不过不久被国际某某组织认定其论文的证明是错误的，我猜测可能段大神，算法是牛逼的，可能在证明自己算法疏忽了细节，不过这个并不会影响我们对段老师的倾佩。此算法的核心就是利用队列去无限的逼近最优解，算法的主题和广度优先遍历算法大体一样，不同于广度优先遍历，出队顶点时，这个点还有可能再次入队。

吐槽下，我按照算法思路写出两类代码(网上算法步骤分为两派)去和网上大佬们对比，发现网上各种代码的百分之99都是存在严重问题的，因为，它们对于这个SPFA的约束问题没搞清楚。也可能是老师当年没完善吧，假设图中无负权回路，SPFA算法在求解带负权的无向图是不成立的，在求解带负权的有向图是正确的。这个当时我电脑测试了自己的一个版本，当时还不行，又进行了手绘图测试，发现带负权的无向图还是有BUG。大家有空可以测试下。希望大佬指点。

算法描述

初始化队列，将源点入队列。设置辅助数组dis初始化为无穷大,数组temp初始化为0,数组path初始化为-1,其中dis数组存储源点到其它点的距离，temp数组存储对应点是否在队列里，path数组存储对应到源点的最短路径。(path和迪杰斯特拉的path原理一样)，设置源点下标对应的dis值为0(自己到自己的距离是0)，设置源点下标对应的temp值为1(源点在队列里)
出队一个点point,设置该点在temp数组的值是0(代表该点出队列),遍历其它所有点i，凡是存在(dis[i]>dis[point]+point到i的距离)，就修改点i的在dis数组的值是dis[point]+point到i的值，并将该点入队列，更新temp数组的i的值为1.更新path数组对用i的值是point(代表该点的前驱点是point)
循环执行步骤2，直到队列为空。

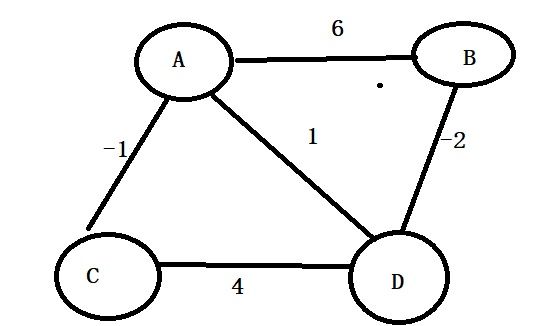
举例分析整个过程,我们假设A是源点(起点)

tree27.jpg

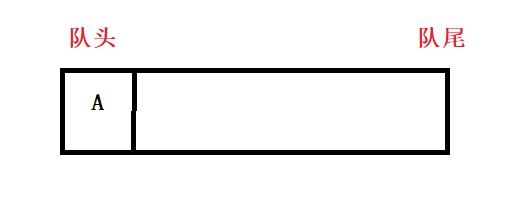
1.初始化队列，dis数组，temp数组，path数组，让源点A入队列,修改A的temp是1，A的dis值是0，此时的数组情况和队列情况如下图

顶点信息	A	B	C	D
顶点下标	0	1	2	3
dis数组	0	∞	∞	∞
temp数组	1	0	0	0
path数组	-1	-1	-1	-1

queue6.jpg

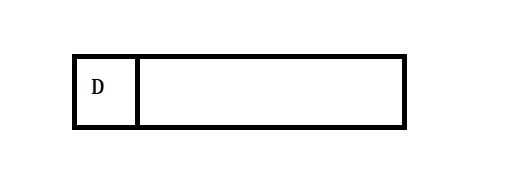
2.出队列队头A，更新temp[0]=0(出队),并逐个与其它点判断(松弛操作),首先是B，发现dis[1]>dis[0]+AB的距离,(此处的dis[1]和dis[0]对应的就是点B，点A，我们用顶点下标代替点)所以修改dis[1] = dis[0]+AB = 6,入队点B，更新temp[1] = 1,path[1] = 0,接着是点C,发现dis[2]>dis[0]+AC，于是修改dis[2] = dis[0]+AC=-1,入队点C，更新path[2] = 0,temp[2] = 1,最后来到了点D,发现dis[3]

顶点信息	A	B	C	D
顶点下标	0	1	2	3
dis数组	0	6	-1	∞
temp数组	0	1	1	0
path数组	-1	0	0	-1

queue7.jpg

3.出队队头B，更新temp[1] = 0,逐个判断与其它点，首先是A，dis[0]dis[1]+BD,修改dis[3]=dis[1]+BD=4,发现D未在队列，让D入队，修改path[3]=1,temp[3]=1。更新后的如下图

顶点信息	A	B	C	D
顶点下标	0	1	2	3
dis数组	0	6	-1	4
temp数组	0	0	1	1
path数组	-1	0	0	1

queue8.jpg

4.出队队头C，更新temp[2]=0,逐个点判断，首先是A，dis[0]dis[2]+CD,修该dis[3]=dis[2]+CD=3,发现D在队列里，更新path[3] = 2。更新后的如下图

顶点信息	A	B	C	D
顶点下标	0	1	2	3
dis数组	0	6	-1	3
temp数组	0	0	0	1
path数组	-1	0	0	2

queue9.jpg

5.出队队头D，更新temp[3]=0,逐个点判断，首先A是源点，dis[0]

顶点信息	A	B	C	D
顶点下标	0	1	2	3
dis数组	0	6	-1	3
temp数组	0	0	0	0
path数组	-1	0	0	2

queue10.jpg

此时的数组就是点A到其它点的最短距离和最短路径了。path数组存储的时路径，看查看方式和迪杰斯特拉一样，我们举一个例子。AD的最短距离，我们查看dis数组dis[3] = 3。
AD的最短路径是path[3]=2,中间点是2,path[2]=0,中间点是0，path[0]=-1,没点了。
所以AD的最短路径就是A-C-D

代码

void SPFA(struct MGraph *g, char obj)
{
    int index,i,*queue,*visit,*dis,*path,front,rear,top;
    queue = (int*)malloc(sizeof(int)*100);//防止队列溢出(此处的队列非循环队列)
    visit = (int*)malloc(sizeof(int)*g->numVretexes);
    dis = (int*)malloc(sizeof(int)*g->numVretexes);
    path = (int*)malloc(sizeof(int)*g->numVretexes);
    //1.找出源点
    for (i = 0; i < g->numVretexes; i++)
    {
        if (g->vetex[i] == obj)
        {
            index = i;
        }
    }
    //2:初始化队列,辅助数组
    for (i = 0; i < g->numVretexes; i++)
    {
        visit[i] = 0;
        dis[i] = MAX;
        path[i] = -1;
    }
    front = rear = 0;
    queue[rear++] = index;
    visit[index] = 1;
    dis[index] = 0;
    while (rear != front)//队列空结束
    {
        top = queue[front++];
        visit[top] = 0;
        for (i = 0; i < g->numVretexes; i++)
        {
            if (i != top)
            {
                if (dis[i] > (dis[top] + g->data[top][i]))
                {
                    dis[i] = dis[top] + g->data[top][i];
                    path[i] = top;
                    if (visit[i] == 0)//没在队列里,入队
                    {
                        queue[rear++] = i;
                        visit[i] = 1;
                    }
                }
            }
        }
    }
    //输出最端距离和路径
    for (i = 0; i < g->numVretexes; i++)
    {
        if (i != index)
        {
            printf_s("%c-->%c(%d)\n", g->vetex[index], g->vetex[i], dis[i]);
        }
    }
}

弗洛伊德算法

弗洛伊德算法是求图中每个顶点之间的最短路径算法，它的思想是利用动态规划去得到问题的解。理解起来就是对图中所有两个顶点对，依次采取松弛操作，找到最优解。

算法描述

首先准备两个二维数组dis和path,dis数组存储图中两个点的距离，path数组存储两个点对应的路径，初始dis就是对应点之间的距离，初始path全部是-1。
对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是就更新它。(自己到自己的顶点对肯定不用判断)
状态转移方程
如果dis[u][v]>dis[u][w]+dis[w][v]成立

则：dis[u][v]=dis[u][w]+dis[w][v],,,,,path[u][v] = path[u][w]

看下面的图，我们来分析下

tree28.jpg

1.初始化dis和path数组

dis	0	1	2	3
0	0	6	-1	1
1	6	0	∞	-2
2	-1	∞	0	4
3	1	-2	4	0

path	0	1	2	3
0	-1	-1	-1	-1
1	-1	-1	-1	-1
2	-1	-1	-1	-1
3	-1	-1	-1	-1

2.图中所有顶点对有(0,1)(1,0)(0,2)(2,0)(0,3)(3,0)(1,2)(2,1)(1,3)(3,1)(2,3)(3,2)对于以上每一个顶点对，对经过点0(A)的松弛判断，根据状态转移方程进行修改dis和path的值。首先(0,1)顶点对中间点是0的松弛判断，dis[0][1]=dis[0][0]+dis[0][1],所以状态方程不成立。因为此图是无向图，所以(0,1)(1,0)顶点对判断一个就行了。接着(0,2)中间点还是0,dis[0][2]=dis[0][0]+dis[0][2]还是不成立。接着(0,3)此时dis[0][3]=dis[0][0]+dis[0][3]还是不成立，接着(1,2)发现dis[1][2]>dis[1][0]+dis[0][2];所以设置dis[1][2]=dis[1][0]+dis[0][2]=5,并更新path[1][2] =0;并同步更新(2,1)的dis数组和path数组。接着来到(1,3),dis[1][3]dis[2][0]+dis[0][3],所以修改dis[2][3]=dis[2][0]+dis[0][3]=0,并更新path[2][3]=0;，同步修改(3,2)的dis数组和path数组,如下表

dis	0	1	2	3
0	0	6	-1	1
1	6	0	5	-2
2	-1	5	0	0
3	1	-2	0	0

path	0	1	2	3
0	-1	-1	-1	-1
1	-1	-1	0	-1
2	-1	0	-1	0
3	-1	-1	0	-1

3.接下来还是顶点对(0,1)(1,0)(0,2)(2,0)(0,3)(3,0)(1,2)(2,1)(1,3)(3,1)(2,3)(3,2),对于每一个顶点对经过点1(B)的松弛判断

dis	0	1	2	3
0	0	6	-1	1
1	6	0	5	-2
2	-1	5	0	0
3	1	-2	0	0

path	0	1	2	3
0	-1	-1	-1	-1
1	-1	-1	0	-1
2	-1	0	-1	0
3	-1	-1	0	-1

4.经过点2(C)的松弛判断

dis	0	1	2	3
0	0	4	-1	-1
1	4	0	5	-2
2	-1	5	0	0
3	-1	-2	0	0

path	0	1	2	3
0	-1	2	-1	2
1	2	-1	0	-1
2	-1	0	-1	0
3	2	-1	0	-1

5.经过点3(D)的松弛判断

dis	0	1	2	3
0	0	-3	-1	-1
1	-3	0	-2	-2
2	-1	-2	0	0
3	-1	-2	0	0

path	0	1	2	3
0	-1	3	-1	2
1	3	-1	3	-1
2	-1	3	-1	0
3	2	-1	0	-1

此时dis数组和path数组全部更新完毕，现在dis数组存储的是两个点之间的最短距离，path数组对应的就是两个点间的路径过程。这个path查看路径是个递归的过程。

核心代码

//Floyd算法
void Floyd(struct MGraph *g)
{
    int i, j, k,temp=0;
    int **dis, **path;
    dis = (int**)malloc(sizeof(int*) * g->numVretexes);
    path = (int**)malloc(sizeof(int*) * g->numVretexes);
    for (i = 0; i < g->numVretexes; i++)
    {
        dis[i] = (int*)malloc(sizeof(int) *g->numVretexes);
        path[i] = (int*)malloc(sizeof(int) *g->numVretexes);
    }
    //初始化dis和path数组
    for (i = 0; i < g->numVretexes; i++)
    {
        for (j = 0; j < g->numVretexes; j++)
        {
            dis[i][j] = g->data[i][j];
            path[i][j] = -1;
        }
    }
    //开始逐个点p的判断
    for (i = 0; i < g->numVretexes; i++)
    {
        //逐个取出每两个点x,y，判断dis[x][y] > dis[x][p]+dis[p][y]
        for (j = 0; j < g->numVretexes; j++)
        {
            for (k = 0; k < g->numVretexes; k++)
            {
                if (dis[j][k] > dis[j][i] + dis[i][k])
                {
                    dis[j][k] = dis[j][i] + dis[i][k];
                    path[j][k] = i;
                }
            }
        }
    }

    //输出最短距离
    for (i = 0; i < g->numVretexes; i++)
    {
        for (j = 0; j < g->numVretexes; j++)
        {
            if (i != j)
            {
                //printf_s("%c-->%c(%d)", g->vetex[i], g->vetex[j], dis[i][j]);
                print_Path(i, j, g, path);
                printf("%d\n", dis[i][j]);
            }
        }
    }
}

获取完整代码

我分别用C，C++，JAVA三种主流语言编写了完整代码，请大家指导批正，一起学习。

点击查看