二叉树(js实现)
二叉树
- 基本概念
-
- 基本术语
- 二叉树类型
- 性质
- 遍历
-
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 二叉搜索树
- 镜像二叉树
- 重建二叉树
- 其它常见算法题
-
- 求二叉树深度
- 二叉树结点总数
- 叶子结点数
- 判断二叉树子结构
- 将二叉搜索树转换成一个排序的双向链表
基本概念
二叉树是n个有限元素的集合,该集合或者为空、或由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成
基本术语
- 结点之间的关系
- 若一个结点有子树,那么该结点称为子树根的双亲,子树的根称为该结点的孩子
- 有相同双亲的结点互为兄弟
- 一个结点的所有子树上的任何结点都是该结点的后裔
- 从根结点到某个结点的路径上的所有结点都是该结点的祖先
- 结点层:根结点的层定义为第一层,根的孩子为第二层,依此类推
- 树的深度:树中最大的结点层
- 结点的度:结点拥有的子树的个数
- 树的度: 树中最大的结点度
- 叶子结点:也叫终端结点,是度为 0 的结点
- 分枝结点:度不为0的结点
二叉树类型
-
完全二叉树
一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下层的叶结点集中在靠左的若干位置上
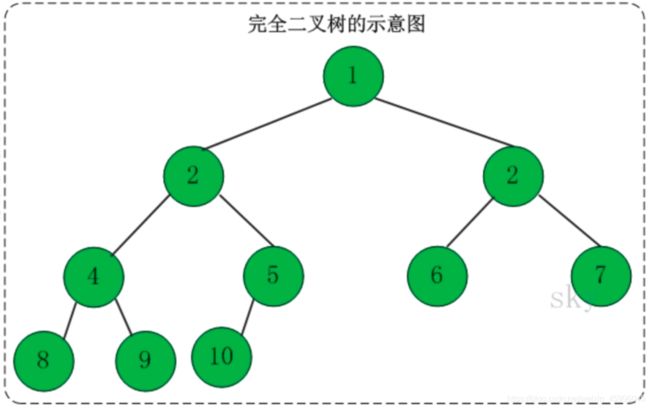
- 判断
思路:一棵完全二叉树,其某结点如果没有左孩子就一定不能有右孩子,且某结点没有左孩子或右孩子则它后面就不能有孩子function isCompleteTree(root) { if(!root) return true; var flag = 0; var queue = []; queue.push(root); while(queue.length != 0) { var node = queue.shift(); if(!node.left) flag = 1;//表示后面不能有节点了 else if(node.left && flag == 0) queue.push(node.left); else if(node.left && flag == 1) return false; if(!node.right) flag = 1; else if(node.right && flag == 0) que.push(node.right); else if(node.right && flag == 1) return false; } return true; }
- 判断
-
平衡二叉树
是一棵空树,或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树- 判断一个树是否为平衡二叉树
function maxDepthOfTree(node) { if(!node) return 0; return Math.max(maxDepthOfTree(node.left),maxDepthOfTree(node.right))+1; } function isBalanced(node) { if(!node) return true; var left = maxDepthOfTree(node.left); var right = maxDepthOfTree(node.right); if(Math.abs(left-right) > 1) return false; return isBalanced(node.left) && isBalanced(node.right); }
- 判断一个树是否为平衡二叉树
性质
- 在二叉树的第 i 层上最多有
2^(i-1)个结点(i>=1) - 深度为h的二叉树,最多有
2^h-1个结点,最少有h个结点(h>=1) - 包含n个结点的二叉树的高度至少为
(log2n)+1 - 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则
n0=n2+1
遍历
前序遍历
根结点 -> 左子树 -> 右子树
//递归
function preOrder(root)
{
if(!root)
return;
console.log(root.val);
preOrder(root.left);
preOrder(root.right);
}
//非递归
function preOrder(root)
{
var stack = [];
var node = root;
while(node || stack.length != 0){
//循环访问节点的左子结点并入栈
while(node){
console.log(node.val);
stack.push(node);
node = node.left;
}
if(stack.length != 0){
node = stack.pop();
node = node.right();
}
}
}
中序遍历
左子树 -> 根结点 -> 右子树
//递归
function inOrder(root)
{
if(!root)
return;
preOrder(root.left);
console.log(root.val);
preOrder(root.right);
}
//非递归
function inOrder(root)
{
var stack = [];
var node = root;
while(node || stack.length != 0){
while(node){
stack.push(node);
node = node.left;
}
if(stack.length != 0){
node = stack.pop();
console.log(node.val);
node = node.right();
}
}
}
后序遍历
左子树 -> 右子树 -> 根结点
//递归
function postOrder(root)
{
if(!root)
return;
preOrder(root.left);
preOrder(root.right);
console.log(root.val);
}
//非递归
function postOrder(root)
{
var stack = [];
var node = root;
var lastVisit = null; //标记每次遍历最后一次访问的结点
while(node || stack.length != 0){
while(node){
stack.push(node);
node = node.left;
}
if(stack.length != 0){
node = stack.pop();
//判断节点是否有右子结点,同时判断lastVisit避免重复输出右子结点)
if(node.right == null || node.right == lastVisit){
//如果没有则输出
console.log(node.val);
lastVisit = node;
node = null;
}
else{
//如果有则再次入栈,并访问节点的右子节点
stack.push(node);
node = node.right();
}
}
}
}
层序遍历
用队列实现
function levelOrder(root)
{
var queue = [], res = [];
queue.push(root);
while(queue.length != 0){
let len = queue.length; //一层结点个数
let temp = [];
for(let i = 0; i < len; i++){
var node = queue.shift();
temp.push(node.val);
if(node.left)
queue.push(node.left);
if(node.right)
queue.push(node.right);
}
res.push(temp);
}
return res;
}
二叉搜索树
又称二叉查找树、二叉排序树,其根节点的值大于其左子树中任意一个结点的值,小于其右子树中任意一结点的值,这一规则适用于二叉查找树中的每一个节点
- 建立
function insertTree(node, val) { if(!node){ node = new TreeNode(); node.val = val; node.left = null; node.right = null; return true; } if(node.val == val) return false; if(node.val > val) return insertTree(node.left, val); else return insertTree(node.right, val) } - 查找
function SearchTree(node, val) { if(!node) return null; if(node.val == val) return node; if(node.val > val) return SearchTree(node.left, val); else return SearchTree(node.right, val); }
镜像二叉树
# 源二叉树
8
/ \
6 10
/ \ / \
5 7 9 11
# 镜像二叉树
8
/ \
10 6
/ \ / \
11 9 7 5
-
实现
思想:改变根节点的左右指向即可。需要先知道左右孩子指针,再处理根节点,对应的遍历方式为后序遍历//递归:自下向上换 function Mirror(root) { if(!root) return null; var left = Mirror(root.left); var right = Mirror(root.right); root.left = right; root.right = left; /* 另一种写法: Mirror(root.left); Mirror(root.right); [root.left, root.right] = [root.right, root.left]; */ return root; } //非递归:从上向下换 function Mirror(root) { if(!root) //不加这个root为null时会报错 return root; var a = []; //队列 a.push(root); while(a.length != 0){ var l = a.length; for(var i = 0; i < l; i++){ var node = a.shift(); //压出第一个元素 if(node.left) a.push(node.left); if(node.right) a.push(node.right); //左右指针交换 [node.left, node.right] = [node.right, node.left]; } } return root; } -
判断是否为镜像
function isMirror(node1, node2) { if(node1 == null && node2 == null) return true; if(node1 == null || node2 == null) return false; if(node1.val != node2.val) return false; return isMirror(node1.left, node2.right) && isMirror(node1.right, node2.left); } isMirror(root.left, root.right);
重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树
- 思路
- 确定根结点,前序遍历的第一个结点为根节点
- 确定两种遍历方式的左右子树顺序
- 在左子树中递归步骤1和2
- 在右子树中递归步骤1和2
- 打印当前根
function reConstructBinaryTree(pre, vin)
{
// write code herepre
if(pre.length == 0 || vin.length == 0)
return null;
var index = vin.indexOf(pre[0]); //根结点在中序遍历中的位置
var vinLeft = vin.slice(0, index); //中序左子树
var vinRight = vin.slice(index+1); //中序右子树
var preLeft = pre.slice(1, index+1); //前序右子树
var preRight = pre.slice(index+1); //前序左子树
var root = new TreeNode(pre[0]);
root.left = reConstructBinaryTree(preLeft, vinLeft);
root.right = reConstructBinaryTree(preRight, vinRight);
return root;
}
其它常见算法题
求二叉树深度
function depth(node)
{
if(!node)
return 0;
return Math.max(depth(node.left), depth(node.right))+1;
}
二叉树结点总数
function getNodeNumber(node)
{
if(!node)
return 0;
return getNodeNumber(node.left)+node(node.right)+1;
}
叶子结点数
function getLeafNum(node)
{
if(!node)
return 0;
if(!node.left && !node.right)
return 1;
return getLeafNum(node.left)+getLeafNum(node.right);
}
判断二叉树子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(ps:约定空树不是任意一个树的子结构)
- 思路
- 判断步骤
- 在树A中找到和B的根结点的值一样的结点R
- 判断树A中以R为根结点的子树是不是包含和树B一样的结点
- 递归终止条件
- 如果树B为空,返回
true,此时,不管树A是否为空,都为true - 如果树B不为空,但是树A为空,返回
false
- 如果树B为空,返回
- 判断步骤
function dfs(pRoot1, pRoot2) //先序遍历判断子树结构
{
if(!pRoot2) //B树空了不管A树为不为空都返回true
return true;
if(!pRoot1) //A树空了B树没空返回false
return false;
if(pRoot1.val !== pRoot2.val)
return false;
return dfs(pRoot1.left, pRoot2.left) && dfs(pRoot1.right, pRoot2.right);
}
function HasSubtree(pRoot1, pRoot2)
{
var flag = false;
if (pRoot1 == null || pRoot2 == null)
return false;
if (pRoot1.val == pRoot2.val) //如果根结构相等,判断子树结构
flag = dfs(pRoot1, pRoot2);
/*
如果当前A树根结点与B树根结点不相等或根节点相等但子树结构不同,
先序遍历A树其它节点作为根结点与B树进行比较
*/
if(!flag)
flag = HasSubtree(pRoot1.left, pRoot2);
if(!flag)
flag = HasSubtree(pRoot1.right, pRoot2);
return flag;
}
将二叉搜索树转换成一个排序的双向链表
- 思路
因为二叉搜索树是左子树的所有节点比根节点小,右子树的所有节点比根节点大,所以如果要转换成一个有序的双向链表应该以中序遍历:左子树 -> 根节点 -> 右子树的顺序遍历二叉树,进行递归 - 解法1
- 先用递归中序遍历二叉树并将结果保存在list中
- 遍历list修改指针指向
- 解法2
- 递归,先将左子树调整为双向链表,并用变量pLast指向最后一个节点
- 再将中间节点和pLast连起来
- 再去调整右子树
- 最后返回最后一个节点,再向前移到第一个节点并返回
//1.
function Convert(pRootOfTree)
{
// write code here
if(!pRootOfTree)
return null;
var list = new Array();
ConvertNode(pRootOfTree, list); //中序遍历
for(let i = 0; i < list.length - 1; i++){
//注意是list.length-1
list[i].right = list[i+1];
list[i+1].left = list[i];
}
return list[0];
}
function ConvertNode(root, list)
{
if(root.left)
ConvertNode(root.left, list);
list.push(root);
if(root.right)
ConvertNode(root.right, list);
}
//2.
function Convert(pRootOfTree) {
// write code here
if(!pRootOfTree)
return null;
var pLast = null;
pLast = ConvertNode(pRootOfTree, pLast); //最后一个节点
var pHead = pLast;
while (pHead.left) {
//移到第一个节点
pHead = pHead.left;
}
return pHead;
}
function ConvertNode(pNode, pLast) {
if(pNode.left){
pLast = ConvertNode(pNode.left, pLast);
}
pNode.left = pLast; //该节点的left指针指向上一个节点
if (pLast) {
//上一个节点的right指针指向下一个节点
pLast.right = pNode;
}
pLast = pNode;
if (pNode.right) {
pLast = ConvertNode(pNode.right, pLast);
}
return pLast;
}
参考:
① https://blog.csdn.net/qq_36332184/article/details/102775099
② https://blog.csdn.net/xiaoquantouer/article/details/65631708
③ https://www.cnblogs.com/chenrencun/p/13569596.html
④ https://blog.csdn.net/weixin_39318565/article/details/111594445