层次分析法——python
原理
层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成–个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
步骤和方法
Step1.建立层次结构模型

!注意:准则层的因素间应相互独立
例:旅游地选择层次结构模型
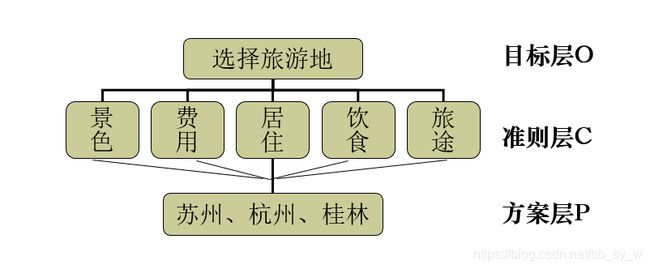
Step2.构造成对比较矩阵
构造比较矩阵是通过比较同一层次上的各因素对上–层相关因素的影响作用.而不是把所有因素放在一起比较,即将同一层的各因素进行两两对比。
构造比较矩阵是通过比较同一层次上的各因素对上一层相关因素的影响作用.而不是把所有因素放在一起比较,即将同一层的各因素进行两两对比。
设某层有n个因素,X = {x1,x2…xn}要比较它们对上一层某一准则(或目标)的影响程度,确定在该层中相对于某一准则所占的比重。
上述比较是两两因素之间进行的比较,比较时常取1~9尺度。

成对比较矩阵(未减少主观性,可以加入主成分分析)

Step3.层次单排序及一致性检验
(1)相对权重向量确定



(2)一致性检验
通常情况下,由实际得到的判断矩阵不一-定是- -致的,即不一定满足传递性和一-致性.实际中,也不必要求一致性绝对成立, 但要求大体上是一致的,即不一致的程度应在容许的范围内主要考查以下指标:
一致性指标:
随机一致性指标RI,通常由实际经验给定的:

一致性比率指标: CR=CI/RI, 当CR≤0.10时, 认为对比矩阵的一 致性是可以接受的,则Amax对应的特征向量W可以作为排序的权重向量。此时
否则要调整成对比较矩阵。
Step4.计算组合权重和组合一致性检验
(1)计算组合权重
设第K1层上Nk-1个元素对总目标(最高层)的排序权重向量为:

第k层上Nk个元素对上一层(K- 1层)上第j个元素的权重向量为:





代码实例
假期某人想要出去旅游,现有三个目的地(方案):山水甲天下的桂林(P1)、迷人的黄山( P2)和风光绮丽的北戴河( P3)。假如选择的标准和依据(行动方案准则)有5个景色, 费用,饮食,居住和旅途。
Step1.建立层次结构模型
Step2.构造成对比较矩阵
这里暂时主观确定准则层权重矩阵(权重可以结合其他方法客观确定)
"""
AHP demo: 第一层:A, 第二层:B1 B2 B3,B4,B5 第三层:C1 C2 C3, 完全相关性结构。
"""
import numpy as np
from scipy.sparse.linalg import eigs
'''
构造准则层成对比较矩阵
'''
def compmatix(W0): # W为每个信息值的相对权重
n=len(W0)
F=np.zeros([n,n])
for i in range(n):
for j in range(n):
if i==j:
F[i,j]=1
else:
F[i,j]=W0[i]/W0[j]
return F
w = np.array([0.2,0.4,0.16,0.12,0.12])
cpm = compmatix(w)
构造相对于不同准则层的方案判断矩阵
'''
层次单排序,构造所有相对不同准则的方案层的判断矩阵
'''
#权重向量
w1 = np.array([10/17,5/17,2/17])#相对于景色
w2 = np.array([1/12,1/4,2/3])#相对于费用
w3 = np.array([3/7,3/7,1/7])#相对于居住
w4 = np.array([12/19,4/19,3/19])#相对于饮食
w5 = np.array([1/6,1/6,2/3])#相对于旅途
#成对比较矩阵
pm = np.zeros((5,3,3))
i = 0
for col in [w1,w2,w3,w4,w5]:
pm[i] = compmatix(col)
i+=1
Step3.层次单排序(计算组合权重)及(组合)一致性检验
'''
组合一致性检验
'''
def isConsist(F):
n=np.shape(F)[0]
a,b=eigs(F,1)
maxlam=a[0].real
CI=(maxlam-n)/(n-1)
RI = np.array([0,0,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59])#实际经验,可查表。
CR =CI/RI[n-1]
if CR<0.1:
return bool(1)
else:
return bool(0)
def ComImpo(pmatx,cpmatx):
if isConsist(pmatx[0]) and isConsist(pmatx[1]) and isConsist(pmatx[2]) and isConsist(pmatx[3]) and isConsist(pmatx[4]) and isConsist(cpmatx) :
print("一致性检验通过!")
else:
print("成对比较矩阵不一致,请调整权重后重试!")
return 0
ComImpo(pm,cpm)
Step4.层次总排序
"""
层次总排序
"""
W = np.dot(p.T,cp)
print('最佳方案为第',np.argmax(W)+1,'个方案.','综合推荐指数为',W.max())